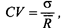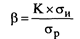Распределения вероятностей и ожидаемая доходность
Поскольку риск связан с вероятностью того, что фактическая доходность будет ниже ее ожидаемого значения, распределения вероятностей являются основой для измерения риска. Предположим, например, что вы финансовый менеджер фирмы, которая решила инвестировать 100 000 долларов сроком на один год. В таблице 1 приведены четыре альтернативных варианта инвестиций:
1. Казначейские векселя (Т-векселя) со сроком погашения один год и ставкой дохода 8%, которые могут быть приобретены с дисконтом (т.е. по цене ниже номинала); в момент погашения будет выплачена их номинальная стоимость.
2. Корпорационные облигации, которые продаются по номиналу с купонной ставкой 9% (т.е. на 100 000 долларов вложенного капитала можно получать 9000 долларов годовых) и сроком погашения 10 лет. Однако ваша фирма планирует продать эти облигации в конце первого года. Следовательно, фактическая доходность по облигациям будет зависеть от уровня процентных ставок на конец года. Этот уровень в свою очередь зависит от состояния экономики на конец года: быстрые темпы экономического развития, вероятно, вызовут повышение процентных ставок, что снизит рыночную стоимость облигаций, в случае экономического спада возможна противоположная ситуация.
3. Проект капиталовложений №1, чистая стоимость которого составляет 100 000 долларов. Денежный поток в течение года равен нулю, все выплаты осуществляются в конце года. Сумма этих выплат зависит от состояния экономики.
4. Альтернативный проект капиталовложений №2, совпадающий по всем параметрам с проектом №1 и отличающийся от него лишь распределением вероятностей ожидаемых в конце года выплат.
Распределением вероятностей называется множество возможных исходов с указанием вероятности появления каждого из них. Таким образом, в таблице 1 представлены четыре распределения вероятностей, соответствующие четырем альтернативным вариантам инвестирования. Доходность по казначейским векселям точно известна — она составляет 8% и не зависит от состояния экономики. Таким образом, риск по казначейским векселям равен нулю.
Отметим, что инвестиции в казначейские векселя являются безрисковыми только в том смысле, что их номинальная доходность не изменяется в течение данного периода времени. Реальная же доходность казначейских векселей содержит определенную долю риска, поскольку она зависит от фактических темпов роста инфляции в течение периода владения векселями. Более того, казначейские векселя могут представлять проблему для инвестора, который обладает портфелем ценных бумаг с целью получения непрерывного дохода: когда истекает срок платежа по казначейским векселям, необходимо осуществить реинвестирование денежных средств и если процентные ставки снижаются, доход портфеля также уменьшится.
Этот вид риска, который носит название риска нормы реинвестирования, не учитывается в нашем примере, так как период, в течение которого фирма владеет векселями, соответствует сроку их погашения. Наконец, отметим, что релевантная доходность любых инвестиций — это доходность после уплаты налогов, поэтому, значения доходности, используемые для принятия решения, должны отражать доход за вычетом налогов.
По трем другим вариантам инвестирования реальные, или фактические, значения доходности не будут известны до окончания соответствующих периодов владения активами. Поскольку значения доходности не известны с полной определенностью, эти три вида инвестиций являются рисковыми.
Оценка доходности по четырем инвестиционным альтернативам
| Таблица 1 | |||||
| Доходность инвестиций при данном состояния экономики, % | |||||
| Состояние экономики | Вероятность | Казначейские векселя, % | корпорационные облигации | проект №1 | проект №2 |
| Глубокий спад | 0,05 | 80 | 12,0 | — 3,0 | — 2,0 |
| Незначительный спад | 0,20 | 80 | 10,0 | 6,0 | 9,0 |
| Стагнация | 0,5 | 80 | 9,0 | 11,0 | 12,0 |
| Незначительный подъем | 0,20 | 80 | 8,5 | 14,0 | 15,0 |
| Сильный подъем | 0,05 | 80 | 8,0 | 19,3 | 26,0 |
| ____________________________________________________________________________________ | |||||
| Ожидаемая доходность | — | 80 | 9,2 | 10,3 | 12,0 |
Примечание. Доходность, соответствующую различным состояниям экономики следует рассматривать как интервал значений, а отдельные ее значения — как точки внутри этого интервала. Например, 10%-ная доходность облигации корпорации при незначительном спаде представляет собой наиболее вероятное значение доходности при данном состоянии экономики, а точечное значение используется для удобства расчетов.
Распределения вероятностей бывают дискретными или непрерывными. Дискретное распределение вероятностей имеет конечное число исходов; так, в таблице 1 приведены дискретные распределения вероятностей. Доходность казначейских векселей принимает только одно возможное значение, тогда как каждая из трех оставшихся альтернатив имеет пять возможных исходов. Каждому исходу поставлена в соответствие вероятность его появления. Например, вероятность того, что казначейские векселя будут иметь доходность 8%, равна 1.00, а вероятность того, что доходность казначейских корпоративных облигаций составит 9%, равна 0.50.
Если умножить каждый исход на вероятность его появления, а затем сложить полученные результаты, мы получим средневзвешенную исходов. Весами служат соответствующие вероятности, а средневзвешенная представляет собой ожидаемое значение. Так как исходами являются доходности, ожидаемое значение — это ожидаемая доходность (expected rate of return, k), которую можно представить в следующем виде:
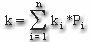
ki — i-й возможный исход,
Рi — вероятность появления i-го исхода,
n — число возможных исходов.
Используя формулу, находим, что ожидаемая доходность проекта 2 равна 12.0%
к = -2.0% * 0.05 + 9.0% * 0.20 + 12.0% * 0.50 + 15%* 0.20 + 26.0% * 0.05 = 12.0%
Ожидаемые доходности трех других альтернативных вариантов инвестирования найдены аналогичным образом (таблице 1).
Дискретные распределения вероятностей могут быть представлены графически или в табличной форме. На рисунке 1 приведены столбиковые диаграммы (или гистограммы) проектов №1 и №2.
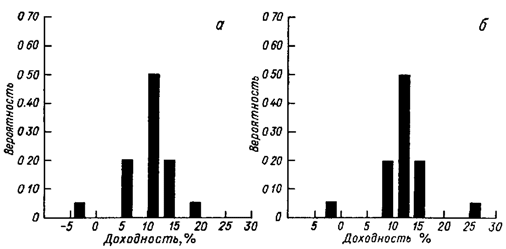
Рисунок 1. Графическое представление дискретного распределения вероятностей; а — проект №1; б — проект №2
Возможные значения доходности проекта №1 принадлежат промежутку от -3.0 до +19.0%, а проекта №2 от -2.0 до +26.0%. Отметим, что высота каждого столбца представляет собой вероятность появления соответствующего исхода, а сумма этих вероятностей по каждому варианту равна 1.00. Отметим также, что распределение значений доходности проекта №2 симметрично, тогда как соответствующее распределение для проекта №1 имеет левостороннюю асимметрию. Аналогичные диаграммы для казначейских векселей и корпорационных облигаций показали бы, что доходность казначейских векселей представлена единственным столбцом, а доходность корпорационных облигаций представлена диаграммой, имеющей правостороннюю асимметрию.
Программная реализация данной методики финансовой математики сделана в: «Альтаир Финансовый калькулятор 2.xx».
На примере расчета ожидаемой доходности можно увидеть, как применять программу «Альтаир Финансовый калькулятор 2.xx» на практике.

Главная 



Copyright © 2021 by Altair Software Company. Потенциальным спонсорам программ и проекта.
Источник
Ожидаемая доходность акций
В сфере инвестирования ожидаемая доходность (англ. Expected Rate of Return) представляет собой процентную ставку или сумму, которую инвестор ожидает получить в течение определенного периода времени от вложений в определенный актив. С практической точки зрения этот показатель может быть рассчитан исходя из полного набора вероятностей, либо на основе исторических данных о доходности актива.
Формула
В случае, если заранее известен полный набор вероятностей, то есть вероятности всех возможных вариантов исхода событий, ожидаемую доходность можно рассчитать использовав следующую формулу:

где Pi – вероятность наступления i-го исхода событий;
ki – доходность при i-ом исходе событий;
n – количество исходов событий.
В условиях реального финансового рынка инвестор, как правило, принимает решение на основании имеющейся информации об исторической доходности ценной бумаги. В этом случае ожидаемая доходность рассчитывается как среднеарифметическое:

ki – доходность ценной бумаги в i-ом периоде;
n – количество наблюдений.
Пример расчета
Пример 1. Финансовый аналитик рассматривает возможность включения в портфель инвестора одной дополнительной акции, выбирая из трех компаний, работающих в сфере оптово-розничной торговли. При этом он рассматривает три возможных сценария развития событий, вероятность и предполагаемая доходность которых представлены в таблице.
Чтобы определить ожидаемую доходность каждой из ценных бумаг, необходимо воспользоваться первой из приведенных выше формулой. Для акций Компании А она составит 11,25%, акций Компании Б 12,4% и акций Компании В 12,9%.



Если не принимать во внимание прочие факторы (например, риск), то в портфель инвестора целесообразно включить акции Компании В, поскольку они характеризуются самой высокой ожидаемой доходностью.
Пример 2. Финансовому аналитику необходимо оценить ожидаемую доходность акций на основании данных об их исторической доходности за последние 7 недель, которые представлены в таблице.
Поскольку аналитику известна только историческая доходность акций, необходимо воспользоваться второй из приведенных выше формул.



Источник
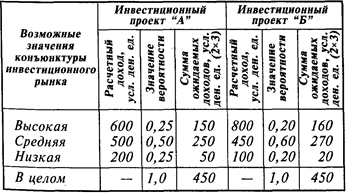
Распределение вероятности ожидаемых доходов по двум инвестиционным проектам
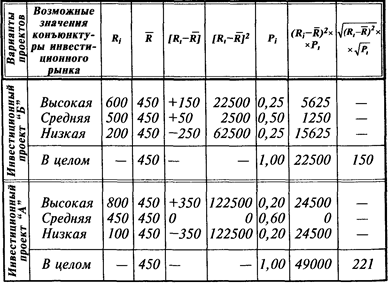
Более наглядное представление об уровне риска дают результаты расчета среднеквадратического (стандартного) отклонения, представленные в табл. 3.3.
Расчет среднеквадратического (стандартного) отклонения по двум инвестиционным проектам
Результаты расчета показывают, что средне-квадратическое (стандартное) отклонение по инвестиционному проекту «А » составляет 150, в то время как по инвестиционному проекту «Б» — 221, что свидетельствует о большем уровне его риска.
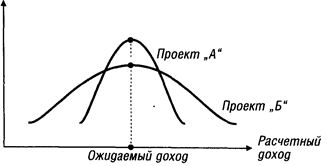
Рассчитанные показатели среднеквадратического (стандартного) отклонения по рассматриваемым инвестиционным проектам могут быть интерпретированы графически (рис. 3.11.)
Из графика видно, что распределение вероятностей проектов «А » и «Б » имеют одинаковую величину расчетного дохода, однако в проекте «А » кривая уже, что свидетельствует о меньшей колеблемости вариантов расчетного дохода относительно средней его величины R, а следовательно и о меньшем уровне риска этого проекта.
Рисунок 3.11. Распределение вероятности ожидаемого (расчетного) дохода по двум инвестиционным проектам.
г) Коэффициент вариации. Он позволяет определить Уровень риска, если показатели среднего ожидаемого дохода от осуществления финансовых операций различаются между собой. Расчет коэффициента вариации осуществляется по следующей формуле:
где CV— коэффициент вариации;
σ—среднеквадратическое (стандартное) отклонение;
R—среднее ожидаемое значение дохода по рассматриваемой финансовой операции.
Пример: Необходимо рассчитать коэффициент вариации по трем инвестиционным проектам при различных значениях среднеквадратического (стандартного) отклонения и среднего ожидаемого значения дохода по ним. Исходные данные и результаты расчета приведены в табл 3 4
Расчет коэффициента вариации по трем инвестиционным проектам
Результаты расчета показывают, что наименьшее значение коэффициента вариации — по проекту «А», а наибольшее — по проекту «В» Таким образом, хотя ожидаемый доход по проекту «В» на 33% выше, чем по проекту «А» ((600 – 450) / 450 х 100) , уровень риска по нему, определяемый коэффициентом вариации, выше на 61% )(0,53 – 0,33) / 0,33 х 100)
Следовательно, при сравнении уровней рисков по отдельным инвестиционным проектам предпочтение при прочих равных условиях следует отдавать тому из них, по которому значение коэффициентов вариации самое низкое (что свидетельствует о наилучшем соотношении доходности и риска).
д) Бета-коэффициент (или бета) Он позволяет оценить индивидуальный или портфельный систематический финансовый риск по отношению к уровню риска финансового рынка в целом. Этот показатель используется обычно для оценки рисков инвестирования в отдельные ценные бумаги. Расчет этого показателя осуществляется по формуле:
К — степень корреляции между уровнем доходности по индивидуальному виду ценных бумаг (или по их портфелю) и средним уровнем доходности данной группы фондовых инструментов по рынку в целом;
σи — среднеквадратическое (стандартное) отклонение доходности по индивидуальному виду ценных бумаг (или по их портфелю в целом);
σр — среднеквадратическое (стандартное) отклонение доходности по фондовому рынку в целом.
Уровень финансового риска отдельных ценных бумаг определяется на основе следующих значений бета-коэффициентов:
Источник