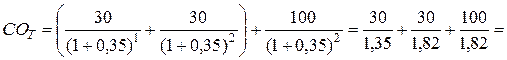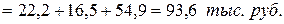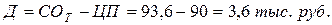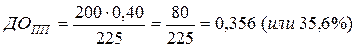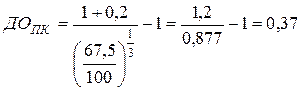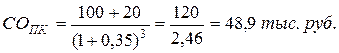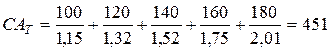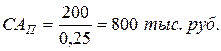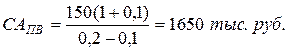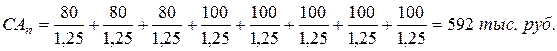Ожидаемая текущая доходность задачи
Доходность акций определяется двумя факторами: получением части распределяемой прибыли в форме дивидендов, возможностью продать ценные бумаги по цене больше цены приобретения.
Iд — дивидендный доход
iд — ставка дивиденда
Рн — номинальная цена акции
Отношение дохода к инвестируемым средствам, выраженное коэффициентом или в %-тах, называется доходностью (или рендитом) и характеризует рентабельность капитала, вложенного в финансовые активы .
Рпр -цена приобретения
Если акция продана в середине фин-ого года, сумма дивиденда делится между прежним и новым владельцем бумаг по формуле точных %-тов.
t — срок владения ценных бумаг в текущем году
Дополнительный доход при росте курса акций или убыток при падении курса можно определить в абсолютных единицах или %-х
Iддi — дополнительный доход,
Рр — курсовая цена акции
I = R + iдд (общая доходность)
Рыночная цена акции в расчёте на 100 д.е. номинала называется курсом акции
1. АО зарегистрировало 10 тыс. обыкновенных акций, из которых 9 тыс. было продано акционерам. Через некоторое время ОАО выкупило у инвесторов 500 акций. По окончании отчётного года собранием акционеров было принято решение о распределении в качестве дивидендов 170 тыс. р. прибыли. Определить дивиденд на 1 акцию
2. УК АО в размере 10 млн. р. разделён на 900 обыкновенных и 100 привилегированных акций. Предполагаемый размер прибыли к распределению — 200 т.р. Фиксированная ставка дивидендов по привилегированным акциям — 20%. Определить размер дивиденда, на получение к-ого может рассчитывать владелец обыкновенной и привилегированной акции.
10 000 / (100+900) = 10 т.р. — номинал акции
10 * 0,2 = 2 т.р. — дивиденд на привилегированную акцию
2*100 = 200 т.р. — дивиденды по всем привилегированным акциям
200 — 200 = 0 (получает владелец обыкновенной акции)
3. Акция номиналом 10 рублей куплена по курсу 25, по ней выплачивается дивиденд 50%. Определить текущую доходность инвестируемых средств.
10*0,5 = 5 р. — дивидендный доход
5/25 = 0,2 или 20% — текущая доходность
4. Курсовая цена акции размещённой по номиналу 10 р. в первый год после эмиссии составила 20 рублей. Определить дополнительную доходность бумаги.
(20 -10)/10 *100% = 100 %
5. Акция приобретена по номиналу 10 р. при 40% годовых, курсовая цена после эмиссии 20 р. Определить конечную доходность бумаги.
(20-10)/10 + 40% = 140%
6. Акция номиналом 10 рублей куплена с коэффициентом 1,7 и продана владельцем на 3 год после приобретения за 90 дней до даты выплаты дивидендов. В первый год уровень дивиденда составил 15 р., во второй доходность оценивалась в 20%, в третий ставка дивиденда — 45%. Индекс динамики цены продажи по отношению к цене приобретения 1,25. Нужно определить совокупную доходность за весь срок со дня приобретения до дня продажи.
10*1,7 = 17 — цена приобретения
15+0,2*17+4,5 (265-90)/365 = 21,79 (дивидендный доход)
17*12,5 -17 = 4,25 (дополнительный доход)
21,79 + 4,25 = 26,04 — общий доход
26,04/17 = 1,53 (общая доходность)
7. Определить зависимость курсовой цены от ставки дивиденда (прямо пропорциональная) и от ставки банковского %-та (обратно-пропорциональная).
Источник
Примеры решения задач. Ожидаемая доходность и стандартное отклонение
Ожидаемая доходность и стандартное отклонение. Этот пример позволит вам на практике рассчитать показатели, которые мы можем ожидать от инвестиционного портфеля. Даны два вида акций и три состояния экономики:
| Состояние экономики | Вероятность такого состояния | Уровень доходности ценных бумаг типа A | Уровень доходности ценных бумаг типа B |
| Спад | 0,1 | -0,2 | 0,3 |
| Нормальное | 0,6 | 0,1 | 0,2 |
| Подъем | 0,3 | 0,7 | 0,5 |
Рассчитайте стандартное отклонение и ожидаемую доходность для каждого типа акций.
Риск портфеля и доходность. Вернемся к примеру 11.1 и предположим, что всего вы имеете $20000. Если вы вложите $6000 в акции A, а остальное в B, какими будут ожидаемая доходность и стандартное отклонение вашего портфеля?
Риск и доходность. Предположим, что вы рассматриваете следующую ситуацию:
| Ценные бумаги | Бета | Ожидаемая доходность |
| Cooley, Inc. | 1,6 | 19% |
| Moyer Co. | 1,2 | 16% |
Если ставка, свободная от риска, составляет 8%, правильно ли оценены данные ценные бумаги? Какой должна была бы быть ставка, свободная от риска, если ценные бумаги оценить правильно?
CAPM. Предположим, что ставка, свободная от риска, составляет 8%. Ожидаемая доходность на рынке составляет 14%. Если конкретный вид актива имеет (3 = 0,6, то какова ожидаемая доходность этого актива, основываясь на CAPM? Если другой актив имеет ожидаемую доходность 20%, то какой должен быть (3 коэффициент?
Ответы
Ожидаемые доходности рассчитываются как произведение возможных доходностей на их вероятности:
E(RA) = 0,1 х (-0,2) + 0,6 х (0,1) + 0,3 х (0,7) = 25% E(RB) = 0,1 х (0,3) + 0,6 х (0,2) + 0,3 х (0,5) = 30%
Непостоянство рассчитывается как сумма произведений квадратов отклонения ожидаемых доходностей на их вероятности:
Од = 0,1 х (-0,2 — 0,25)2 + 0,6 х (0,1 — 0,25)2 + 0,3 х (0,7 — 0,25)2 = = 0,1 х (-0,45)2 + 0,6 х (-0,15)2 + 0,3 х (0,45)2 = = 0,1 х 0,2025 + 0,6 х 0,0225 + 0,3 х 0,2025 = 0,0945
а2, = 0,1 х (0,3 — 0,3)2 + 0,6 х (0,2 — 0,3)2 + 0,3 х (0,5 — 0,3)2 =
= 0,1 х (0,0)2 + 0,6 х (-0,1)2 + 0,3 х (0,2)2 =
= 0,1 х 0,0 + 0,6 х 0,01 + 0,3 х 0,04 = 0,0180 Стандартные отклонения равны: аА = УО,0945 =30,74% aB = VO,0180 = 13,42%
Вес каждого типа акций в портфеле составляет: $6000/20000 = 0,3 и $14000/20000 = 0,7. Тогда ожидаемая доходность портфеля составит:
Щ/У = 0,3 х E(RA) + 0,7 х E(RB) = 0,3 х 25% + 0,7 х 30% = 28,50%
Мы также могли бы рассчитать доходность портфеля и для каждого состояния экономики:
| Состояние экономики | Вероятность такого состояния | Доходность портфеля |
| Спад | 0,1 | 0,3 х (-0,2) + 0,7 х (0,3) = 0,15 |
| Нормальное | 0,6 | 03х(0,1) + 0,7х(02) = 0,17 |
| Подъем | 0,3 | 03х(0,7) + 07х (0,5) = 0,56 |
Тогда доходность портфеля составляет
E(Rp) = 0,1 х (0,15) + 0,6 х (0,17) — 0 3 х (0,56) = 28,50%.
Это тот же самый результат, что мы получили ранее.
Рассчитаем непостоянство портфеля
Ор = 0,1 х (0,15 — 0,285)2 + 0,6 х (0,17 — 0,285)2 + 0,3 х (0,56 — 0,285)2 = 0,03245
Тогда стандартное отклонение есть корень квадратный из 0,03245 и равно 18,01%
Если мы рассчитаем коэффициент награды за риск для ценных бумаг каждой компании, мы в результате получим (19% — 8%)/1,6 = 6,875% для Cooley и 6,67% для Моуег По отношению к Cooley ожидаемая доходность Моуег слишком низкая, поэтому ее цены слишком высокие
Если ценные бумаги обеих компаний оценены правильно, то они должны предлагать одинаковый коэффициент награды за риск Таким образом, мы можем составить уравнение
(19% — Rj)/],6 = (16% — Rf)/l,2
Произведя небольшие алгебраические преобразования, мы получим /?у= 7%
(19% — Rf) = (16% — ЯД 1,6/1 ,2) 19% — 16% х (4/3) = Rf — Rf x (4/3) йу=7%
Так как рыночная ожидаемая доходность составляет 14%, то рыночная премия риска соответственно (14% — 8%) = 6% (ставка, свободная от риска, равна 8%) Первый вид ценных бумаг имеет Р = 0,6, значит ожидаемая доходность составляет 8% + 0,6×6%= 11,6%
Для второго вида премия риска составляет 20% — 8% = 12% Так как это ровно в два раза превышает рыночную премию риска, то и р коэффициент должен быть точно равен 2 Мы можем проверить это используя теорию CAPM
20% = 8% + [14% — 8%] х р Р, = 12%/6% = 2,0
Вопросы и задачи
Ожидаемые доходности портфеля. Если портфель имеет положительные инвестиции в каждый вид актива, может ли ожидаемая доходность такого портфеля быть больше, чем доходность каждого актива в этом портфеле? Меньше? Если у вас положительный ответ на один или оба вопроса, пожалуйста приведите пример, чтобы аргументировать ваше решение.
Непостоянство индивидуального актива и диверсификация. Правда или нет: наиболее важной характеристикой при определении ожидаемой доходности хорошо диверсифицированного портфеля являются непостоянства индивидуальных активов портфеля. Объясните.
Риск портфеля. Если портфель имеет положительные инвестиции в каждый вид актива, может ли стандартное отклонение такого портфеля быть меньше, чем стандартное отклонение каждого актива в этом портфеле? Что вы можете сказать о b такого портфеля?
Доходности портфеля. Используя информацию предыдущей главы об истории рынка ценных бумаг, определите, какой была доходность портфеля, который былодинаково распределен между обыкновенными акциями и долгосрочными правительственными облигациями? Который одинаково распределен между малыми акциями и векселями Казначейства?
CAPM. Используя CAPM, докажите, что коэффициент премии риска двух активов равен их коэффициентам р.
Доходности портфеля и отклонения. Имея следующую информацию о портфеле, состоящем из трех видов ценных бумаг, определите:
| Состояние экономики | Вероятность такого состояния | Уровень доходности ценных бумаг типа A | Уровень доходности ценных бумаг типа B | Уровень доходности ценных бумаг типа C |
| Подъем | 0,20 | 0,20 | 0,30 | 1,00 |
| Нормальное | 0,70 | 0,10 | 0,05 | 0,30 |
| Спад | 0,10 | 0,00 | -0,20 | -0,80 |
Если вы инвестировали по 30% в A и B, 40% в C, какой будет ожидаемая доходность портфеля? Непостоянство? Стандартное отклонение?
Если ожидаемый уровень доходности T-bill составляет 5,25%, то какой будет премия риска портфеля?
Если ожидаемый уровень инфляции составляет 5%, то какова реальная ожидаемая доходность портфеля? Какова реальная премия риска портфеля?
Анализ портфеля. Вы хотите создать портфель с таким же уровнем риска, что и фондовый рынок в целом. У вас есть $200000. Имея нижеприведенную информацию, заполните недостающие позиции:
| Актив | Инвестиции, $ | b |
| Вид A | 1,20 | |
| Вид B | 0,85 | |
| Вид C | ?? | 1,40 |
| Актив, свободный от риска | ?? | ?? |
Анализ портфеля. Вы имеете $100000 для инвестиций либо в ценные бумаги типа D, либо в F, либо в актив, свободный от риска. Вы должны вложить все ваши деньги. Ваша цель – создание портфеля с ожидаемой доходностью 10% и только с 60% риска, по сравнению с остальным рынком. Если D имеет ожидаемую доходность 20% и Р = 1,50, F имеет ожидаемую доходность 15% и Р = 1,15, ставка, свободная от риска составляет 5%, то сколько денег вы вложите в F?
Систематический риск против несистематического. Вы имеете следующую информацию:
| Состояние экономики | Вероятность такого состояния | Уровень доходности ценных бумаг типа A | Уровень доходности ценных бумаг типа B |
| Спад | 0,15 | 0,14 | -0,18 |
| Нормальное | 0,60 | 0,24 | 0,10 |
| Подъем | 0,25 | 0,28 | 0,40 |
Рыночная премия риска составляет 8% и ставка, свободная от риска, равна 6%. Какой вид ценных бумаг имеет наибольший систематический риск? Какой вид имеет наибольший несистематический риск? Какой вид ценных бумаг наиболее рискованный? Объясните.
Вопросы повышенной сложности
Коэффициенты b. Может ли рискованный актив иметь b = 0? Объясните. Используя модель CAPM, какой будет ожидаемая доходность такого актива? Может ли рискованный актив иметь отрицательный b коэффициент? Что предсказывает CAPM об уровне ожидаемой доходности для такого актива? Можете ли вы пояснить свой ответ?
Линия состояния фондового рынка (SML). Предположим, что вы рассматриваете следующую ситуацию:
| Ценные бумаги компании | b | Ожидаемая доходность |
| Abel Co. | 1,15 | 18% |
| Baker Co. | 0,80 | 15% |
Допустим, что эти ценные бумаги правильно оценены. Основываясь на CAPM, определите, какой будет ожидаемая рыночная доходность? Какова ставка, свободная от риска?
[1] Экзамен CFA – экзамен на получение сертификата финансового аналитика, который выдается специалистам в области инвестиций в США.

Источник
Модели оценки реальной стоимости и ожидаемой доходности фондовых инструментов



С учётом особенностей формирования денежного потока и дифференциации нормы текущей доходности рассмотрим модели оценки реальной стоимости отдельных фондовых инструментов.
Оценка облигаций (сберегательных сертификатов и других аналогичных ценных бумаг) предусматривает решение ряда задач, среди которых важнейшей является определение её текучей рыночной стоимости.
Формула, по которой рассчитывается этот показатель, называется «Основной моделью оценки облигаций» (Basic Bond Valuation Model).
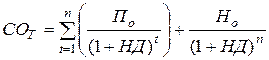
где: СОТ – текущая рыночная стоимость облигации;
По – ежегодная сумма процента по облигации, представляющая собой произведение её номинала на объявленную ставку процента:
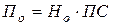
Если сумма процента выплачивается с иной периодичностью (например, раз в полугодие, раз в квартал и т.п.), то расчет по формуле производится с предусматриваемыми периодами выплаты процента;
Но –номинал облигации, подлежащей погашению в конце периода её обращения;
ПС – ставка, по которой будет начислена сумма процента по облигации, в десятичной дроби;
НД – норма текущей доходности, используемая как дисконтная ставка в расчётах настоящей стоимости, в десятичной дроби;
n – число лет (или иных периодов), остающихся до погашения облигации.
Пример: На фондовом рынке предлагается к продаже облигация одной из компаний по цене 90 тыс. руб. за единицу. Она была выпущена сроком на 3 года, до погашения осталось 2 года. Её номинал при выпуске – 100 тыс. руб. Процентные выплаты по облигации осуществляются 1 раз в год по ставке 30 % к номиналу. С учётом уровня риска данного типа облигации норма её текущей доходности – 35 % в год. Определить текущую рыночную стоимость облигации и её соответствие цене продажи (ЦП).
НД = 0,35______
Д – дополнительный доход в связи с заниженной рыночной стоимостью.
I. 1.1. Модель расчёта ожидаемой доходности по облигациям без выплаты процентов
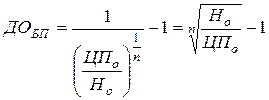
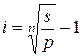
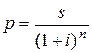
где: ДОБП – ожидаемая доходность по облигации без выплаты процентов, в десятичной дроби;
Но – номинал облигации, подлежащий погашению в конце периода её обращения ;
ЦПо – цена, по которой облигация реализуется на рынке;
n – число лет (или иных периодов), отстающих до погашения облигации.
Экономическое содержание данной модели состоит в том, что уровень ожидаемой доходности по облигациям без выплаты процентов представляет собой дисконтную ставку, по которой номинал облигации приводится к настоящей стоимости, приравненной к цене её реализации.
Пример: Облигация внутреннего местного займа номиналом в 100 тыс. руб. реализуется по цене 67,5 тыс. руб. Погашение облигации предусмотрено
через 3 года. Норма текущей доходности по облигациям такого типа составляет 16 %. Определить ожидаемую доходность по облигации и её соответствие текущей норме доходности облигаций такого типа.
НД = 0,16
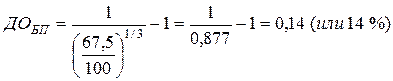
НД — ДОБП = 0,16 – 0,14 = 0,02 уровень доходности ниже среднерыночной на 2 % Þ невыгодна.
1.2. Модель расчёта текущей рыночной стоимости облигаций без выплаты процентов.
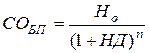
где: СОБП – текущая рыночная стоимость облигаций без выплаты процентов;
Но – номинал облигации, подлежащий погашению в конце периода её обращения;
НД – норма текущей доходности по конкретному виду облигаций (в десятичной дроби);
n – число лет (или иных периодов), остающихся до погашения облигации.
Пример: Определить текущую рыночную стоимость облигации внутреннего местного займа и сопоставить её с ценой продажи, используя данные предыдущего примера.
ЦП – СОБП = 67,5 – 64,1 = 3,4 тыс. руб. Þ цена завышена на 3,4 тыс. руб. Þ невыгодна.
2.1. Модель расчёта ожидаемой текущей доходности по облигациям с периодической выплатой процентов.
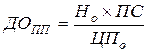
где: ДОПП – ожидаемая текущая доходность по облигации с периодической выплатой процентов, в десятичной дроби;

Но – номинал облигации, к которому начисляется сумма процента;
ПС – ставка, по которой начисляется сумма процента по облигации, в десятичной дроби;
ЦПо – цена, по которой облигация реализуется на рынке.
Необходимость дисконтирования в этом случае отпадает, т.к. оба указанных показателя должны приводиться к настоящей стоимости по единой ставке дисконта, в результате чего их соотношение не изменится.
При расчёте текущей рыночной стоимости таких облигаций используется Основная модель оценки облигаций.
Пример. Облигация компании номиналом Но = 200 тыс. руб. реализуется на рынке по цене ЦПо = 225 тыс. руб. Става ежегодного начисления процентов по ней (купонная ставка). ПС = 0,40. Норма текущей доходности по облигациям такого типа НД = 0,35. Определить ожидаемую текущую доходность по облигации, сопоставив её с нормой текущей доходности.
ДОПП – НД = 0,356 – 0,35 = 0,006 (на 0,6 % превышает нормативную) Þ выгодна.
3.1. Модель расчёта ожидаемой текущей доходности по облигациям с выплатой всей суммы процентов при погашении.
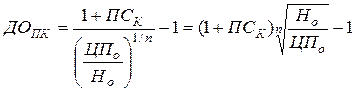
где: ДОПК – ожидаемая текущая доходность по облигации с выплатой всей суммы процентов при погашении, в десятичной дроби;
ЦПо – цена, по которой облигация реализуется на рынке;
Но – номинал облигации, к которому при погашении будет начислена сумма процента;
ПСК – ставка, по которой будет начислена сумма процента по облигации при её погашении, в десятичной дроби.
3.2. Модель расчёта текущей рыночной стоимости облигаций с выплатой всей суммы процентов при погашении.
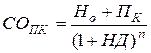
где: СОПК – текущая рыночная стоимость облигации с выплатой всей суммы процентов при погашении;
Но – номинал облигации, подлежащей погашению в конце периода её обращения;
ПК – сумма процента по облигации, которая будет начислена при её погашении по соответствующей ставке;
НД – норма текущей доходности, используемая как дисконтная ставка в расчётах настоящей стоимости, в десятичной дроби;
n – число лет (или иных периодов;, остающихся до погашения облигации.
Пример. Облигация компании номиналом Но = 100 тыс. руб. реализуется на рынке по цене ЦПо = 67,5 тыс. руб. Погашение облигации и разовая выплата суммы процента по ней по ставке ПСК = 20 % предусмотрены через n = 3 года. Норма текущей доходности по облигациям такого типа НД = 0,35. Определить ожидаемую текущую доходность и текущую рыночную стоимость данной облигации.
ЦПо – СОПК = 67,5 – 48,9 = 18,6 тыс. руб. (цена продажи завышена на 18,6 тыс. руб.) Þ невыгодна.
ДОПК – НД = 37 %- 35 % = 2 % — на 2 % выше среднерыночной Þ выгодна.
Вышеперечисленные методы оценки облигаций полностью применимы к расчёту аналогичных показателей по сберегательным сертификатам и другим кредитным ценным бумагам.
Оценка акций направлена прежде всего на определение их текущей рыночной стоимости. Особенно актуальна эта задача в условиях фондового рынка, где рыночная цена продажи акций многих предприятий и банков значительно превышает их реальную текущую рыночную стоимость.
1) Модель оценки текущей рыночной стоимости акции при её использовании в течение неопределённого продолжительного периода времени.
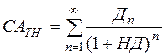
где: САТН – текущая рыночная стоимость акции, используемой неопределённое число лет;
Дn – сумма дивидендов, которую инвестор ожидает получить в n-ом году;
НД – норма текущей доходности акций данного типа, используемая как дисконтная ставка в расчётах настоящей стоимости, в десятичной дроби;
n – число лет, включённых в расчёт.
Пример. Приобретенная инвестором акция представляется инвестору перспективной и намечена им к использованию в течение продолжительного периода. На ближайшие пять лет им составлен прогноз дивидендов, в соответствии с которым в первый год сумма дивидендов составит 100 тыс. руб., а в последующие годы будет ежегодно возрастать на 20 тыс. руб. Норма текущей доходности акций данного типа составляет 15 % в год. Определить текущую рыночную стоимость акции.
2) Модель оценки текущей рыночной стоимости акций при их использовании в течение заранее предусмотренного срока:
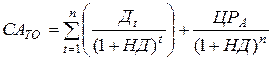
где: САТО – текущая рыночная стоимость акции, используемой в заранее предусмотренный период;
Дt – сумма дивидендов, которую инвестор ожидает получить в t-ом году;
ЦРА – прогнозируемая рыночная цена реализации акции в конце периода её использования;
НД – норма текущей доходности акций данного типа, используемая как дисконтная ставка в расчётах настоящей стоимости, в десятичной дроби;
n –число лет использования акции.
Экономическое содержание данной модели аналогично Основной модели оценки облигаций.
3) Модель оценки текущей рыночной стоимости акций с постоянными дивидендами:
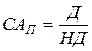
где: САП – текущая рыночная стоимость акции с постоянными дивидендами;
Д – годовая сумма постоянного дивиденда;
НД – норма текущей доходности акций данного типа, в десятичной дроби.
Пример. По акции выплачивается ежегодный постоянный дивиденд в сумме Д = 200 тыс. руб. Норма текущей доходности акций данного типа составляет 25 % в год. Найти текущую рыночную стоимость акции.
4) Модель оценки текущей рыночной стоимости акций с постоянно возрастающими дивидендами («модель Гордона»).
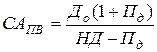
где: САПВ – текущая рыночная стоимость акции с постоянно возрастающими дивидендами;
До – сумма последнего уплаченного дивиденда;
НД – норма текущей доходности акций данного типа, в десятичной дроби;
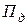
Пример. Последний дивиденд, выплаченный по акции, составлял До=150 тыс. руб. Компания постоянно увеличивает сумму ежегодно выплачиваемых дивидендов на 10 %. Норма текущей доходности акций данного типа – 20 % в год. Найти текущую рыночную стоимость акции. САПВ — ?
5) Модель оценки текущей рыночной стоимости акций с изменяемой суммой дивидендов по периодам.
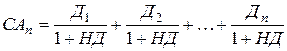
где: САn – текущая рыночная стоимость акции с изменяемой суммой дивидендов;
Дn – сумма дивидендов, прогнозируемая в n-ом периоде;
НД – норма текущей доходности акций данного типа, в десятичной дроби;
n – число прогнозируемых лет.
Пример. В соответствии с принятой дивидендной политикой компания ограничила выплату дивидендов в предстоящие три года суммой 80 тыс. руб. в год. В последующие пять лет она обязалась выплачивать постоянные дивиденды в размере 100 тыс. руб. в год. Норма текущей доходности акций данного типа составляет 25 % в год. Текущая рыночная стоимость акций составит:
Модели оценки реальной рыночной стоимости и текущей доходности отдельных фондовых инструментов используются при их выборе и включении в формируемый инвестиционный портфель.
Источник