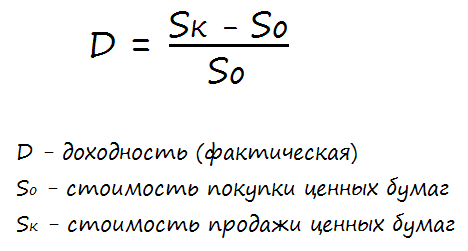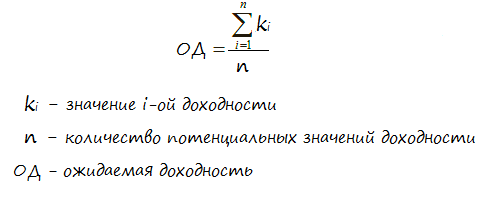Ожидаемая доходность рынка как определить

Ожидаемая доходность акций

В сфере инвестирования ожидаемая доходность (англ. Expected Rate of Return) представляет собой процентную ставку или сумму, которую инвестор ожидает получить в течение определенного периода времени от вложений в определенный актив. С практической точки зрения этот показатель может быть рассчитан исходя из полного набора вероятностей, либо на основе исторических данных о доходности актива.

Формула

В случае, если заранее известен полный набор вероятностей, то есть вероятности всех возможных вариантов исхода событий, ожидаемую доходность можно рассчитать использовав следующую формулу:

(1)

где P_i – вероятность наступления i-го исхода событий;

k_i – доходность при i-ом исходе событий;

n – количество исходов событий.

В условиях реального финансового рынка инвестор, как правило, принимает решение на основании имеющейся информации об исторической доходности ценной бумаги. В этом случае ожидаемая доходность рассчитывается как среднеарифметическое:

(2)

k_i – доходность ценной бумаги в i-ом периоде;

n – количество наблюдений.

Пример расчета

Пример 1. Финансовый аналитик рассматривает возможность включения в портфель инвестора одной дополнительной акции, выбирая из трех компаний, работающих в сфере оптово-розничной торговли. При этом он рассматривает три возможных сценария развития событий, вероятность и предполагаемая доходность которых представлены в таблице.

Чтобы определить ожидаемую доходность каждой из ценных бумаг, необходимо воспользоваться первой из приведенных выше формулой. Для акций Компании А она составит 11,25%, акций Компании Б 12,4% и акций Компании В 12,9%.

_А = 0,25*18+0,5*12+0,25*3 = 11,25%

_Б = 0,3*22+0,45*14+0,25*(-2) = 12,4%

_В = 0,2*35+0,45*17+0,35*(-5) = 12,9%

Если не принимать во внимание прочие факторы (например, риск), то в портфель инвестора целесообразно включить акции Компании В, поскольку они характеризуются самой высокой ожидаемой доходностью.

Пример 2. Финансовому аналитику необходимо оценить ожидаемую доходность акций на основании данных об их исторической доходности за последние 7 недель, которые представлены в таблице.

Поскольку аналитику известна только историческая доходность акций, необходимо воспользоваться второй из приведенных выше формул.

_А = (-2,3+7+4,1-3,4+6,2+4,5+1,8)/7 = 2,56%

_Б = (4,1-5,7+2,4+4,8-1,2+1,1+0,3)/7 = 0,83%

_В = 0,2*35+0,45*17+0,35*(-5) = 0,64%

Источник

Расчет рыночной доходности

Формула расчета рыночной доходности

Любому, кто занимается вложением средств, необходимо уметь грамотно рассчитывать доходность — как для собственных нужд, так и для правильного прочтения различных источников, где указываются результаты инвестиций. В самом простом случае — банковского депозита — рост дохода происходит по прямой линии и сложных расчетов не требуется.

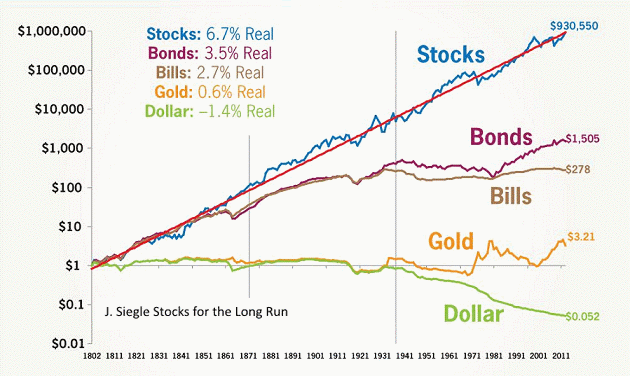
Однако если мы возьмем банковский депозит с возможностью капитализации процентов, то картина уже изменится: счет начнет расти по экспоненте. Аналогичный, но более сильный эффект дает инвестирование на фондовом рынке в акции (логарифмическая шкала):

Вообще говоря, в сети нетрудно найти калькулятор сложного процента — но подойдет он отнюдь не для каждой задачи и поскольку содержит формулу в закрытом виде, то не дает понимания о сути расчета. Непонимание работы с рыночными данными способно привести к ошибкам даже в самых простых случаях. Ниже мы рассмотрим, как посчитать доходность в процентах для разных случаев.

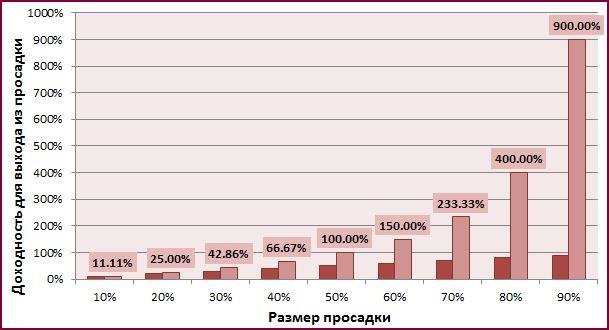
Из этого следует очень важное правило: чем выше просадка, тем большая доходность требуется, чтобы ее отыграть . К примеру, если стоимость актива за год уменьшилась на 80% (осталось только 20% начальной цены), то требуется доходность в целых 400%, чтобы достичь первоначального уровня:

Именно поэтому агрессивные стратегии с высоким кредитным плечом не живут долго — математическое ожидание даже при большей вероятности прибыли, чем убытка все равно со временем уничтожит депозит.

В общем случае формула доходности выглядит так:

A(n) = A(n-1) × (1 + X) = A(0) × (1 + X)^n или X = (A(2)/A(0))^(1/n) – 1

1. A(0) – исходное количество денег
2. А(n) – количество денег через n лет
3. X – годовая доходность (в процентах)

Если же взять изменение за год в разах (Y) (т.е. мы рассматриваем изменение на 10% как рост в 1,1 раза, Y = 1 + 10/100 = 1,1), то

A(n) = A(n-1) × Y = A(0) × Y^n

Задача

Актив растет на 10% в год. Какова будет его доходность через 2 года?

Можно искать калькулятор сложного процента, а можно сказать, что Y = 1.1, число лет n = 2. Тогда взяв исходное количество денег за условную единицу

А(2) = 1 × 1.1² = 1.21, т.е. актив вырастет на 21% (из 1000 рублей будет 1210)

Обратная задача

Найти среднюю годовую доходность при росте актива на 21% в течение двух лет (понятно, что она может расти неравномерно — мы же найдем среднюю величину):

Снова принимая нашу первоначальную доходность за условную единицу, считаем:

Y = (1.21/1)½ = 1.1, т.е. усредненная доходность равна 10%

Задача 2

За четыре года банковский вклад с ежегодной капитализацией прибыли вырос от 100.000 рублей до 150.000 рублей. Какова средняя доходность в годовом исчислении?

Y = (150.000/100.000)^(1/4) = 1.10668, т.е. средняя годовая доходность равна 10.67%

Соответственно, просто разделив 50% на 4 мы получили бы среднеарифметическую доходность 12.5%, что неверно. Эта разница и есть преимущество сложного процента: без него доходность каждый год начислялась бы на 100.000 рублей — т.е. каждый год мы получали бы 12.500, что за четыре года и даст ровно 50.000. Однако при ежегодной капитализации мы добиваемся того же результата уже с меньшим процентом (10.67%).

Задача 3

За 2 года и 6 месяцев стоимость пая в инвестиционном фонде выросла на 42.7% (допустим, пай стоил 5 рублей, а стал стоить 7.135 рубля — значит, 7.135/5 = 1.427). Какова средняя доходность фонда в год?

2 года и 6 месяцев это 2.5 года (n = 2.5), а Y = 1.427. Тогда

Y = (1.427/1)^(1/2.5) = 1.1528, т.е. средняя годовая доходность равна 15.28%

Если за «n» обозначить количество месяцев (n = 30), то теперь можно вычислить и среднемесячную доходность (1.427^(1/30) = 1.0119 или 1.19%. При этом среднеарифметическая доходность была бы 42.7/30 = 1.4233%). Если мы возьмем банковский депозит, где капитализация происходит ежемесячно, то считать надо в месяцах, если ежегодно — то в годах.

Задача 4

Значение индекса ММВБ на конец декабря 1997 года – 85.05 пунктов. Значение индекса ММВБ на конец 2007 года – 1888.86 пунктов. Какова среднегодовая доходность индекса ММВБ за 10 лет?

Y = (A(2)/A(0))^(1/n) = (1888.86/85.05)^(1/10) = 1.3635 или 36.35%

Задача 5

Ниже дана российская инфляция за 2000-2007 годы. Нужно рассчитать среднегодовую.

2000 г. – 20,2%
2001 г. – 18,6%
2002 г. – 15,1%
2003 г. – 12,0%
2004 г. – 11,7%
2005 г. – 10,9%
2006 г. – 9,0%
2007 г. – 11,9%

Это как раз случай, хорошо приближенный к реальности — доходность фондового рынка можно смотреть как по разнице пунктов за выбранный промежуток времени, так и считать (или брать из справочника) по годам. Тогда общий рост потребительской корзины:

1,202 × 1,186 × 1,151 × 1,120 × 1,117 × 1,109 × 1,090 × 1,119 = 2,777 раза (или на 177%)

И средняя инфляция

Y = (A(2)/A(0))^(1/n) =2.777^(1/8) = 1.1362 или 13.62%

P.S. Задача аналогично может быть использована для расчета средней доходности активов, которая за год бывает отрицательной. В этом случае коэффициент берется меньше 1, например при доходности минус 10% в год он равен 1 — 10/100 = 0.9.

Задача 6

Инвестор входит в некоторый счет, который показывает в текущий момент 1500%. Выходит из него через полгода, когда показатель достигает 1700%. Пусть он инвестировал 500 долларов и получил 70% от роста котировок. Каков его доход в % годовых и по абсолютной величине?

Это не 200%, умноженные на 0.7! Считаем: (1 + 1700/100)/(1 + 1500/100) и получаем 1.125, т.е. 12.5% за полгода. Следовательно, среднеарифметически в год будет в два раза больше, а среднегеометрически 1.125^(1/0.5) = 26.56%. Хотя такой расчет в этом случае не будет корректен — мы экстраполируем прибыль, т.е. считаем не только имеющийся, но и будущий результат.

Как видно, в этом случае среднегеометрическая доходность получается выше среднеарифметической — так что таким приемом иногда пользуются инвестиционные фонды, экстраполируя удачные квартальные результаты на целый год. Если же нужно рассчитать доход на 500 долларов за время инвестирования, то сначала учтем, что инвестор получает лишь 70% от роста, т.е. 12.5% × 0.7 = 8.75%. Следовательно, прибыль равна 500 × 8.75% / 100% = 43.75 долларов.

Похожий пример: вошли в счет на отметке доходности в 30%, вышли на 90%. При этом прибыль инвестора увеличилась не в три раза, а на (1 + 90/100)/(1 + 30/100) ≈ 1.46, т.е. примерно на 46%. Если взять 500 долларов, инвестированные в счет, то суммарный баланс составит примерно 730 долларов (прибыль около 230 $).

Задача 7

Расчет доходности акций с учетом дивидендов и курсового роста стоимости. Пусть была куплена акция одной компании за 120 рублей. Спустя какое-то время по ней получены дивиденды 7.2 рубля, а котировки выросли до 135 рублей — после чего акцию продали. Рассчитать полученный доход.

Y = [(7.2 + (135-120))/120] × 100% = 18.5%

Задача 8

По данным предыдущего примера рассчитать доходность в процентах годовых, если на момент продажи акции (достижения ее стоимости 135 рублей) прошло 250 дней:

Y = [(7.2 + (135-120))/120] × 365/250 × 100% = 27.01%

Источник

Доходность ценных бумаг. Основные методы оценки и прогнозирования

Ни для кого не секрет, что основной целью инвестиций в ценные бумаги является получение максимально возможной прибыли при сохранении приемлемого уровня риска. В этой статье я расскажу вам о том, какие виды ценных бумаг обладают потенциально большим потенциалом доходности. Вы узнаете о том из чего складывается их доходность и каким образом она вычисляется. Наконец, мы с вами подробно поговорим о том, как можно провести предварительную оценку и рассчитать ожидаемую доходность ценных бумаг ещё на этапе их выбора.

Какие бумаги потенциально самые прибыльные

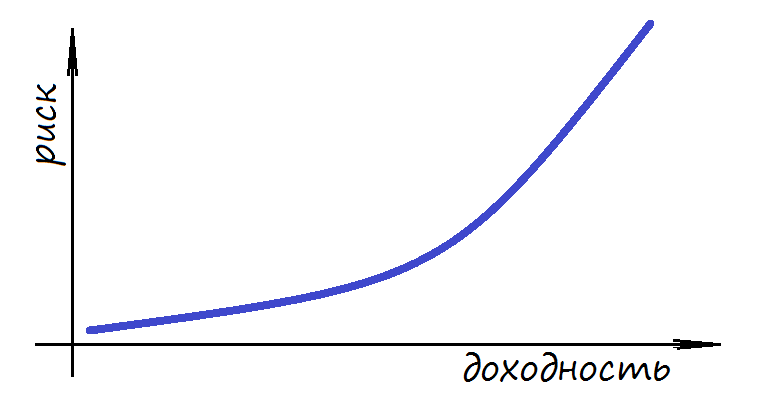
Ответ на этот вопрос довольно прост: самый большой потенциал в плане прибыли имеют ценные бумаги с таким же большим уровнем риска. Чем выше риск, который готов взять на себя инвестор, тем выше тот доход, который он может в итоге получить. Ключевое слово в данном случае – «может», поскольку с увеличением степени риска вероятность получения дохода постепенно тает.

Соотношение риска и доходности

То есть, другими словами, увеличивая степень риска инвестор одновременно и повышает свою потенциальную доходность, и снижает вероятность её получения. Поэтому в инвестициях так важно найти ту самую золотую середину, тот уровень риска при котором можно рассчитывать на относительно высокую прибыль с достаточно большой вероятностью её получения.

Минимальным риском, но и наименьшей степенью доходности отличаются такие бумаги, как государственные облигации. Обычно процент по ним сопоставим с доходностью банковских депозитов и едва превышает текущий уровень инфляции. Инвестирование в бумаги данного типа целесообразно в тех случаях, когда основной целью является не приумножение, а сохранение своих денежных средств.

На ступеньку выше стоят корпоративные облигации крупнейших компаний. Они также обладают достаточной степенью надёжности, но позволяют получить чуть большую прибыль (в отличие от бумаг выпущенных государством). Ещё выше по доходности – акции тех же самых компаний, но и риск по ним тоже чуть выше. Облигация по природе своей — долговая ценная бумага, то есть она подразумевает возврат долга и процентов по нему в любом случае. А вот акция — бумага долевая. Она даёт своему владельцу долю в бизнесе компании её выпустившей, но вместе с этим он принимает на себя и определённые риски (в частности, убытки в результате возможного снижения курса акций).

Ещё более рисковыми, но и потенциально более доходными являются акции и облигации выпущенные не столь известными и не столь крупными компаниями. При этом, чем менее известна компания, тем большую прибыль она вынуждена обещать по своим облигациям (иначе никто не захочет их покупать) и тем сильнее могут в итоге «выстрелить» её акции. Ведь согласитесь, что у автосервиса за углом вашего дома, потенциал к возможному росту куда выше чем, например, у Газпрома или Сбербанка. Автосервис может увеличиться в тысячи раз развивая свой бизнес в сеть по всему городу, по всей стране или, в конце концов, даже по всему миру (вовсе не обязательно что он это сделает, но, тем не менее, теоретическая возможность этого ведь существует). А вот Газпром это уже и так достаточно крупная организация и вряд ли он сможет увеличить свою рыночную капитализацию даже в 5-10 раз.

Есть ещё такие бумаги как фьючерсные и опционные контракты. Торговля ими осуществляется с использованием кредитного плеча (левериджа) и, соответственно, размер потенциальной прибыли в данном случае гораздо выше, он прямо пропорционален размеру предоставляемого плеча. Аналогичным образом растёт и риск.

Предположим, что вы решили приобрести фьючерс на акции IBM. Спецификация данного фьючерсного контракта подразумевает его торговлю с размером левериджа 1 к 10. То есть, при цене одной акции в 135 долларов, обладая суммой в 1350$, вы можете приобрести не десять, а сто таких акций. Хотя если говорить точнее, в данном случае вы приобретёте не сами акции IBM, а фьючерсный контракт на их покупку. Но сути дела это сильно не меняет, ведь по истечении срока данного контракта вы сможете получить прибыль равнозначную той, которая была бы у вас при продаже этих самых акций. Правда при этом и возможный убыток будет равен тому, который вам принесло бы обладание 100 акциями IBM в случае снижения их курсовой стоимости.

Формулы расчёта доходности ценных бумаг

Вообще, доходность по ценным бумагам может складываться из следующих величин:

1. Спекулятивный доход получаемый в результате реализации курсовой разницы при покупке и продаже ценных бумаг;
2. Доход получаемый в виде дивидендов по акциям или в виде процентов по облигациям (купонный доход).

Кроме этого можно говорить о фактической и ожидаемой доходности инвестиций. Фактическая доходность отражает ту величину прибыли, которая была получена, что называется, постфактум. А ожидаемая — показывает ту её величину, которую можно будет получить в будущем.

Про ожидаемую доходность мы поговорим в следующем разделе, а сейчас давайте рассмотрим как рассчитывается фактическая доходность инвестиций в ценные бумаги.

Если речь идёт о чисто спекулятивной доходности (от разницы курсовой стоимости), то её легко можно рассчитать по формуле:

В том случае, если помимо курсовой разницы были получены ещё проценты или дивиденды, доход рассчитывается по формуле:

Обычно доходность рассчитывается в процентах годовых. Для того чтобы привести рассчитанные по вышеприведённым формулам результаты к годовой доходности, следует воспользоваться этой зависимостью:

Ожидаемая доходность ценных бумаг

Грамотное инвестирование в ценные бумаги, предполагает вероятностную оценку рисков и возможностей, выбор допускаемого значения риска и сопоставимого с ним потенциального уровня доходности**. Об инвестиционных рисках и о способах их минимизации мы говорили с вами здесь. А сейчас я расскажу вам о том, как оценить потенциальную доходность ценных бумаг.

Оценить ожидаемую доходность (ОД) можно двумя различными методами. Первый метод основан на вероятностях (математическом ожидании), а второй — на исторических данных. Давайте начнём с вероятностного метода оценки.

** Как мы уже говорили с вами выше, риск и доходность ценных бумаг находятся в прямо пропорциональной зависимости друг от друга. Чем выше риск, тем выше потенциальный уровень доходности и наоборот. Такое положение вещей обусловлено тем, что рынок сам устанавливает данное соотношение, ведь никто не хочет покупать высокорисковые бумаги с небольшим уровнем доходности.

Оценка доходности на основе математического ожидания

В данном случае учитываются все возможные варианты размера предполагаемой доходности вкупе с их вероятностью. Причём наибольший вес придаётся тем значениям, вероятность получения которых выше.

Расчёт производится по формуле:

Для наглядности вычислений, давайте приведём простой пример. Допустим перед инвестором встал выбор из двух бумаг со следующим распределением вероятностей прибылей по ним:

1. Бумага А предположительно принесёт доходность в 10% с вероятностью в 50%, доходность в 7% с вероятностью в 30% или доходность в 4% с вероятностью в 20%;
2. Бумага Б. Вероятность доходности в 12% составляет 30%, вероятность доходности в 8% составляет 35% и вероятность доходности в 5% составляет 35%.

Сначала рассчитываем ожидаемую доходность для бумаги А:

ОД = (0,1*0,5) + (0,07*0,3) + (0,04*0,2) = 0,079 = 7,9%

А теперь рассчитаем ожидаемую доходность для бумаги Б:

ОД = (0,12*0,3) + (0,08*0,35) + (0,05*0,35) = 0,081 = 8,1%

Очевидно, что фактическое значение доходности, скорее всего, будет несколько отличаться от рассчитанного по вышеприведённой формуле. Оценить разброс значений фактических, относительно значений расчётных, можно рассчитав величину дисперсии.

Дисперсия рассчитывается по формуле:

Для нашего примера получим дисперсию для бумаги А:

0,5(0,1 — 0,079) 2 + 0,3(0,07 — 0,079) 2 + 0,2(0,04 — 0,079) 2 = 0,000549

И дисперсию для бумаги Б:

0,3(0,12 — 0,081) 2 + 0,35(0,08 — 0,081) 2 + 0,35(0,05 — 0,081) 2 = 0,000793

Дисперсия показывает тот уровень риска, который повлечёт за собой инвестирование в бумагу для которой была рассчитана ожидаемая доходность на основе вероятностей (математического ожидания). Чем больше дисперсия, тем больше возможное отклонение фактического значения ОД от расчётного.

В нашем примере дисперсия для бумаги Б несколько выше аналогичного показателя для бумаги А. Однако, разница между ними совсем незначительная (не на порядок), поэтому можно считать, что риски рассматриваемых бумаг примерно равны. Следовательно, при прочих равных, инвестирование в бумагу Б является предпочтительным.

Оценка доходности на основе исторических данных

Как вы понимаете, не всегда есть возможность объективно оценить вероятности получения того или иного размера прибыли. Поэтому, на практике часто используют второй метод оценки ОД. Для второго способа расчёта ОД предполагается наличие данных по доходности за несколько равных временных периодов (например, за несколько лет).

Расчёт производится по следующей формуле:

Для примера, давайте опять сравним акции двух компаний А и Б. Для простоты примера возьмём статистику годовой доходности за три последних года. Пускай акции компании А приносили доход в размере:

1. Первый год — 10%;
2. Второй год — 8%;
3. Трети год — 15%.

А акции компании Б:

1. Первый год — 5%;
2. Второй год — 15%;
3. Третий год — 10%.

Подставляя эти значения в формулу получим, для акций компании А:

Для акций компании Б:

Как видите, согласно расчёту, акции компании Б оказываются чуть более выгодными. Однако следует иметь ввиду, что значения доходности в прошлом, не гарантируют её в будущем. Так, в данном примере, на третий год произошло некоторое снижение прибыли. Это может быть вызвано как временными, но преодолимыми трудностями (вызванными, например, изменением конъюнктуры на рынках сбыта), так и свидетельствовать о более серьёзных проблемах компании (наличие которых, скорее всего, повлечёт за собой дальнейшее снижение прибыльности её бумаг).

Источник