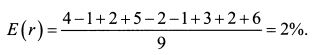Ожидаемая доходность первого актива равна 40

Ожидаемая доходность первого актива равна 40

Аттестаты ФСФР

Экзамены ФСФР

Общение

Полезное

ТЕМА: Решение задач по экзамену 1.0

Re: Решение задач по экзамену 1.0 07.03.2014 23:30 #1834

Инвестор планирует купить акцию компании А и продать ее через два года. Он полагает, что к моменту продажи курс акции составит 100 руб. В конце каждого года по акции будет выплачен дивиденд. За предыдущий год дивиденд был выплачен в размере 4 руб. Инвестор полагает, что темп прироста дивидендов в течение следующих двух лет будет равен 10% годовых. Определить цену акции, если доходность от владения бумагой должна составить 30% годовых.

Ответ: C. 65,42 руб.

Определим цену акции путем дисконтирования всех предполагаемых доходов по ней

P = 4*1,10 / 1,30 + (4*1,10 2 + 100) / 1,30 2 = 65,42 руб.

Re: Решение задач по экзамену 1.0 07.03.2014 23:32 #1835

Roman Вне сайта Модератор Постов: 1117

Портфель состоит из активов X и Y. Инвестор купил актив X на 300 тыс. руб., актив Y на 900 тыс. руб. Стандартное отклонение доходности актива X в расчете на год 20%, актива Y 30%, коэффициент корреляции доходностей активов 0,6. Определить риск портфеля, измеренный стандартным отклонением.

θ_x = 300 / (300+900) = 0,25

θ_y = 900 / (300+900) = 0,75

σ 2 = (0,25*20) 2 + 2*0,6*(0,25*20)*(0,75*30) + (0,75*30) 2 = 666,25

Re: Решение задач по экзамену 1.0 07.03.2014 23:33 #1836

Roman Вне сайта Модератор Постов: 1117

Ожидаемая доходность первого актива равна 40%, второго актива – 30%, стандартное отклонение доходности первого актива составляет 36%, второго актива – 22%, ковариация доходностей первого и второго активов равна нулю. Определить удельного веса бумаг в портфеле с доходностью 32%.

Ответ: A. Удельный вес первого актива 20%, второго 80%

θ₁ = (32-30) / (40-30) = 0,2 = 20%

Источник

1.1. Ожидаемая доходность портфеля. 1.1.1. Ожидаемая доходность актива

Ожидаемая доходность портфеля рассчитывается на основе ожидаемой доходности активов. Каким образом определяется ожидаемая доходность актива? В этом вопросе можно воспользоваться двумя приемами. Первый состоит в том, чтобы на основе прошлых данных статистики доходности актива рассчитать ее среднеарифметическое значение по формуле:

Данные о доходности актива за прошедшие 9 лет представлены в таблице:

Ожидаемая доходность актива в расчете на год равна:

Второй подход заключается в учете возможного будущего вероятностного распределения доходности актива. Ожидаемая доходность актива в этом случае определяется как среднеарифметическая взвешенная, где весами выступают вероятности каждого события. В сумме все возможные варианты событий должны составлять 100% вероятности. Формулу ожидаемой доходности актива можно записать в следующем виде:

Важно: актуальное предложение по поводу компенсации до 100% комиссии, взимаемой Вашим брокером.

Инвестор полагает, что в будущем году можно ожидать следующего вероятностного распределения доходности акции.

Источник

Ожидаемая доходность первого актива равна 40

Управление портфелем ценных бумаг

Ожидаемая доходность портфеля

Главными параметрами управления портфелем ценных бумаг, которые необходимо определить, являются ожидаемая доходность и риск. Формируя портфель, невозможно точно определить будущую динамику его доходности и риска, поэтому инвестиционный выбор основывается на ожидаемых значениях доходности и риска. Данные величины оцениваются, в первую очередь, на основе статистической информации за предыдущие периоды времени. Так как будущее вряд ли повторит прошлое со 100%-ой вероятностью, то полученные оценки можно корректировать согласно своим ожиданиям развития конъюнктуры.

Ожидаемая доходность портфеля рассчитывается на основе ожидаемой доходности активов.Ожидаемая доходность активов определяется двумя способами. Первый состоит в том, чтобы на основе прошлых данных статистики доходности актива рассчитать ее среднеарифметическое значение по формуле: где D — ожидаемая доходность актива, r — фактическая доходность актива в i-м периоде, n — число периодов наблюдения (периоды имеют одинаковую продолжительность).

Пример. Данные о доходности актива за прошедшие 9 лет представлены в таблице.

Ожидаемая доходность актива в расчете на год равна:

Второй подход заключается в учете возможного будущего вероятностного распределения доходности актива. Ожидаемая доходность актива в этом случае определяется как среднеарифметическая взвешенная, где весами выступают вероятности каждого события. В сумме все возможные варианты событий должный составлять 100%. Формулу ожидаемой доходности в этом случае: где r — ожидаемая доходность актива для i-го события, p — вероятность наступления i-го события.

Пример. Инвестор полагает, что в будущем году можно ожидать следующего вероятностного распределения доходности акции.

Ожидаемая доходность бумаги равна:

Портфель, формируемый инвестором, состоит из нескольких ценных бумаг, каждая из которых обладает своей ожидаемой доходностью. Ожидаемая доходность портфеля определяется как средневзвешенная ожидаемая доходность входящих в него бумаг: где D_р — ожидаемая доходность портфеля, r — ожидаемая доходность ценных бумаг, d — удельный вес в портфеле соответствующей ценной бумаги. Удельный вес ценной бумаги в портфеле рассчитывается как отношение ее стоимости к стоимости всего портфеля.

Пример. Портфель состоит из двух бумаг А и В. Стоимоть бумаги А составляет 300 руб., В — 700 руб. Определим ожидаемую доходность портфеля.

Стоимость портфеля равна
Удельные веса бумаг в портфеле составляют:
Ожидаемая доходность портфеля равна:

Таким образом, если инвестор объединяет в портфеле две бумаги, то значение ожидаемой доходности портфеля будет располагается между значениями ожидаемых доходностей первой и второй бумаг.

Содержание рассылки зависит и чем активнее Вы проявляете свою заинтересованность или иной теме, задаете те или иные вопросы — тем полезнее рассылка будет Пишите

Источник

Арифметика финансового рынка (стр. 7 )

Roman Вне сайта Модератор Постов: 1117

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

Долларовая позиция банка в рублях составляет:

ЫЮтысОолл. • 2Нруб. = 1бЯ. шн. руб.

Позиция по евро в рублях равна:

АООтысевроруб. = 1 4мли. руб.

Уд. вес долларовой позиции и рублях в портфеле составляет: ПОЗИЦИИ по евро в рублях:

Стандартное отклонение доходности портфеля равно: Ср =|о,545: — О. ЗН2 +0.455: -0,52* 5 • 0.38 ■ 0,52 0.S2J «-0,136%.

Для условий задачи 4.86 определить стандартное отклонение доходности портфеля, если банк купил доллары и купил евро.

ар =(о,545? -0,38″ +0,455: 0.52: + 2-0,545-0,455• 0.38• 0,52• 0,82J -0,0423 или 4,23%.

Активы входят в портфель в олинаковых уд. весах. Доказать, что для широко диверсифицированного портфеля его дисперсия приблизительно равна средней ковариании дохолностей активов.

Формулу дисперсии портфеля (4.27) можно предаавить в следующем виде;

Если уд. веса активов в портфеле равны, то формула (4.31 > запишется как:

°1 =Е| — а’ +Z Z —covv

где J — удельный вес бумаги в портфеле;

п2> so) оно приблизится к пулю. У второго слагаемого выражение будет

стремиться к единице. Поэтому формула (4.34) принимает вид:

Средняя доходность фондового индекса равна 15% годовых, стандартное отклонение доходности 24%. Предполагается, что доходность имеет нормальное распределение. Инвестор формирует портфель, копирующий данный индекс. Определить вероятность того, что в следующем году портфель принесет ему убыток.

Инвестор подучи г убыток, если доходность пор|федя окажется меньше 1гуля. Согласно формуле (4.3) вероятность того, что доходность актива окажется меньше нуля равна:

Р(-Ф [• Величина представляет сооои тангенс угла

наклона эффективной границы к оси абсцисс.

соответствующие координатам актива без риска [г.-; 0) и рискованною

ктива [/T^fj j; a*,. J. Величина

Ожидаемая доходность первого актива равна 40%, второго актива — 30%. третьего актива — 20%, стандартное отклонение доходности первого актива составляет 36%. второго актива — 22%. третьего актива — 15%, ковариация доходностей первого и второго активов равна 396. первого и третьего 324. второго и третьего 264. Определить е помощью метода множителей Лафанжа уд. веса бумаг в портфеле с доходностью 32%, который характеризуется наименьшим риском.

Задача сводится к минимизации дисперсии портфеля ( (4.40)

2) сумма уд. весов всех активов равна единице:

Искусственно создается и минимизируется функция Лагранжа в форме:

где L функция Лафанжа; О’ целевая функция; л,, /i, — множители Лагранжа для первого и второго ограничений;

С,. С2 — первое и второе ограничения.

Целевая функция представлена функцией (4.39). Первое ограничение -равенством (4.40). второе — (4.41). В функцию Лагранжа первое и второе ограничения включаем в следующей форме:

В общем виде функция Лафанжа чаиишется как:

i-Ј4^*%+4fЈ^-Ј 1+4Л £ч-4 (4.42)

Затем необходимо найти частые производные функции (4.42) по О,, Я,, Л, и приравнять их к нулю:

Решение системы уравнений (4.43) дает ответ на вопрос, н каких уд. весах необходимо включать бумаги в портфель, чтобы он имел минимальную дисперсию для заданного уровня ожидаемой доходности. Составим функцию Лафанжа:

L = lX^,covi+^ Ififi-

Запишем ее в развернутом виде;

I = 0faf + $l(jl + $1^1 + 29ft cov,_, + 20ft cov, (+20Д cov,

Найдем частные производные функции Лагранжа согласно системе (4.43): [ cL

Подставим в систему уравнений (4.45) цифровые значения задачи:

2вх362 + 202396+203324+Л,4Он Я. =0 2ft 222 + 2й( 396 + + Я\ 30 + Я; = 0 20,15-+20,324+ 20,264 +Я, 20 +Я, =0-

0,40 + ft 30+ (9,20-32 = 0

25920, +1920, + 64805 + 40Я, + /Ц = О 7920. + 9680, + 5280, + ЗОЯ, + А, = О 6480,+5280.-4500^204+^ =0 .

Решим систему уравнений с помошью матричного исчисления. Матрицы А, В и 0 соответственно равны:

Решение системы имеет вил:

Уд. веса бумаг в портфеле равны:

О, =25,5154%, О, -68,9693%, 0, -5,5154%.

Ожидаемая доходность первого актива равна 34%, второго актива — 32%, третьего актива 24%, стандартное отклонение доходности первого актива Составляет 34%, второго актива — 32%, третьего актива — 15%, ковариация ДОХОД-ностей первого и второго активов равна 128, первого и третьего — 288, второго и третьего — 240. Определить с помощью метода множителей Лагранжа уд. веса бумаг в портфеле с доходностью 30%. который характеризуется наименьшим риском.

Составим функцию Лафанжа согласно формуле (4.44) и найлем производные по удельным весам активов и коэффициентам Я и Л.. Получим систему уравнений (4.45). Подставим в нее данные задачи:

‘20,34″ +20,128 + 20,288 + 434 + /*,= 0

20,322+ 20,128 + 20,240 + Л.32 + Я. -0

20,15?+ 20,288 + 20,240 + ^n24 + А = 0-

0,34 4 0,32*0,24 30 = 0

11560, +1280, + 2886», + Щ *■ 0,5 А. = О

1280, 110240. + 2400, +Ш, + 0,5Л, = О

, 2880, + 2400, + 2250, +12Л, +0,5/U = 0 —

Решение системы уравнений дает следующие уд. веса бумаг в портфеле: 0, =33.0572%. 0, =33,6786%, 07 ^33,2643%.

Ожидаемая доходность акта ва X равна 34%, актива У — 32%, актива Z — 24%. стандартное отклонение доходности актива X составляет 34%, акгива У — 32%, актива Z — 15%. ковариация доходностей акгнвов X и Y равна 128. X и Z 288. У’ и Z — 240. Определить с помощью метода множителей Лагранжа уд. веса бумаг в пор|фслс с доходностью 36%, который характеризуется наименьшим риском.

0Х =67.9248%, 0, =65,094%. 02 = 33.019%.

Отрицательное значение уд. веса бумаги Z говорит о том, что следует осуществить короткую продажу данного акгива и купить дополнительное количество бумаг X и Y.

Ожидаемая доходность актива А-равна 24%. актива Y — 16%. актива Z — 12%. стандартное отклонение доходности актива Xсоставляет 14%, актива К — 10%. актива Z — 8%. ковариация доходностей активов X и Y равна 14. X и Z — 44,8- У и Z 56. Определить с помощью метода множителей Лшранжа уд. веса бумаг в портфеле с доходностью 20%. который характеризуется наименьшим риском.

0V -45,5108%. 0>. =63.4675%, 0,=-8,978%.

Для условий задачи 4.97 определить уд. веса в портфеле с доходностью 24%. который характеризуется наименьшим риском. Ответ.

вх 68,5759%. 0, 94,2724%, в-А 62.848%.

Как называется подход Г. Марковна к выбору эффективных портфелей?

Подход I». Марковна называется средне-дисперсионным анализом, поскольку построение эффективных портфелей основано на учете значений ожидаемой, т. е. средней доходности портфелей, и их дисперсий (стандартных отклонений).

У лава 4, доходность и рыск портфели ценных бумаг

Какие теоретические условия должны выполняться па практике, чтобы ПОДХОД Г. Марковна имел практическую значимость?

Чтобы подход Г. Марковиа имел практическую значимость, необходимо выполнение, по крайней мере, одного из следующих двух условий, а) Доход-ность портфелей цепных бумаг распределена нормально. Нормальное распределение полностью определяется его математическим ожиданием и дисперсией и симметрично относительно математического ожидания. Поэтому на основе этих параметров удобно выбирать между разными портфелями: наиболее привлекательным является портфель с наибольшим математическим ожиданием (ожидаемой доходностью) и наименьшей дисперсией (риском). б) Функция полезности инвестора должна быть квадратичной вида:

где £[СГ(>’)] —ожидаемая полезность от инвестиции:

U(г) функция полезности инвестора;

а2 дисперсия доходности инвестиций;

Из формулы (4.46) следует: из двух портфелей с одинаковой ожидаемой доходностью инвестор выберет портфель с меньшей дисперсией: из двух портфелей с равной дисперсией — портфель с большей ожидаемой доходность.

Какое количество исходных данных необходимо рассчитать, чтобы определить оптимальный портфель из 50 активов? Решение. Бели портфель состоит из п активов, то следует определить И ожидаемых

доходиостей и стандартных отклонении и —— — коварианнн. Поэтому оошее

количество исходных данных равно:

Согласно результату (4.47) для определения оптимального портфеля из 50

активов необходимо рассчитать

‘-э^э исходных данных.

Сформулируйте теорему отделения (Separation theorem). Ответ.

Можно дать две формулировки Теоремы отделения.

а) Инвестиционное решение вкладчика, выбор и приобретение

рискованного портфеля на фан и не Марковна, — отделено или не зависит от

финансово о решения проблемы, т. с. финансирования выбранной стратегии с помошью кредитования или заимствования.

б) Выбор рискованною портфеля на границе Марковца не зависит от конкретного уровня риска, на который желает пойти инвестор.

Дайте определение рыночного портфеля.

Рыночный портфель — это портфель, включающий все существующие финансовые инструменты, удельный вес которых в нем равен их удельному весу в совокупной капитализации финансового рынка.

Инвесторы могут формировать заемные и кредитные портфели. Какую форму имеет эффективная ipainma Марковца в координатах ожидаемая доходноеib стандартное отклонение доходности при равенстве процентных ставок по займам и депозитам.

Эффективная граница представляет собой прямую линию, коюрая проходит через ставку без риска и рыночный портфель.

Нарисуйте iрафик эффективной границы в координатах ожидаемая доходность стандартное отклонение доходное! и при различии процентных ставок по займам и депозитам.

Эффективная граница состоит из ipex участков и представлена кривой r;A/|’V/:F. г, — ставка по безрисковым депозитам. rh — ставка но займам. ВС

эффективная 1раница Марковца.

Глава 5. Модели оценки стоимости актимт

ГЛАВА 5. МОДЕЛИ ОЦЕНКИ СТОИМОСТИ АКТИВОВ 5.1. Модель оценки стоимости активов (САРМ)

(лавка без риска равна 10%. ожидаемая доходность рыночного портфеля 20%, стандартное отклонение доходности рыночного портфеля — 15%. Определить ожидаемую доходность портфеля, стандартное отклонение доходности которого составляет 30%.

Ожидаемая доходность портфеля определяется с помощью уравнения CMI.:

а — риск / — го портфеля, для которого определяется уровень ожидаемой

li\r,) — ожидаемая доходность / — то портфеля; А (5.4)

Глава 5. Модели оценки стоимости активов

Согласно (5.4) бета портфеля равна:

Рр =0.5-0.8 + 0,3-1.1^0,2-1.3 = 0.99.

Ставка без риска равна 10%. ожидаемая доходность рыночною портфеля 20%, бета акции компании А относительно рыночного портфеля — 1,2. Определить ожидаемую доходность акции.

Ожидаемая доходность акции определяется с помощью уравнения SML:

Действительная ожидаемая доходность акции А больше равновесной, поэтому акция недооценена. Действительная ожидаемая доходность акции В меньше равновесной, поэтому акция переоценена.

Ожидаемая доходность рыночного портфеля 20%, ставка без риска 10% годовых. Коэффициент бега акции компании А относительно рыночного портфеля равен 1,3. Цена акции А 15 руб. Инвестор ожидает, что через год цепа акции составит 17.2 руб., и на акцию будет выплачен дивиденд в 1 руб. Определить, стоит ли инвестору купить акцию А.

Согласно уравнению S. ML равновесная ожидаемая доходность акции равна:

Б(г,) = 1О + 1,3(2О-10) = 23%.

Действительная ожидаемая доходность акции на основе прогнозов инвесчора составляет:

Глава 5. Модели оценки стоимости актинов

Действительная ожидаемая доходность акции меньше равновесной, поэтому бумага переоценена. Следовательно, ее не стоит покупать, так как цена ее должна упасть.

В таблице представлены доходности бумаг Л и В и рыночного индекса за пять лет:

Написать уравнение SML для бумаг А и В относительно рыночного индекса, если ставка без риска равна 10% годовых. Определить ожидаемые доходности бумаг в следующем году, если доходность индекса составит! 5%. В расчетах использовать выборочные. дисперсии и ковариации.

Согласно (4.1) выборочная дисперсия доходности рыночного портфеля равна о*

=41,2. Согласно (4.9) коэффициенты выборочной ковариации доходностей акции А и В и рыночного портфеля соответственно равны eovAn=63 и covftw=32.6. Согласно (5.2) коэффициенты бета акций составляю! рЛ = 1.529 , рп — 0,791. Согласно (5.5) уравнения SML бумаг А и В имеют вид:

Ожидаемые доходности бумаг в следующем году для доходности индекса 15% составят:

А-(г4) = Ю + 1,52915 = 17,645% , Я(гя) = 10+0,79115 = 13,955°/о.

В таблице представлены доходности бумаг Л и В и рыночного индекса за пять лет:

Источник