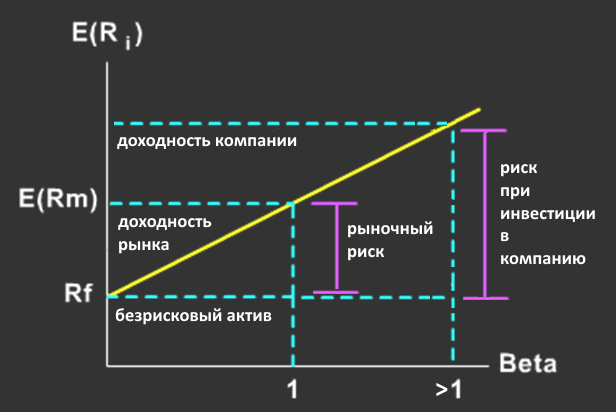
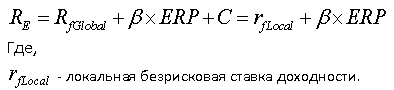САРМ. Модель ценообразования активов (Capital Asset Pricing Model)
Распространенным подходом к оценке уровня премий за акционерный риск, применяемым на практике основными инвестбанками и аудиторами, является модель САРМ (Capital Asset Pricing Model), другое название – модель ценообразования на рынке капитальных финансовых активов, изредка в учебной литературе встречается аббревиатура МОДА, то есть «модель оценки долгосрочных активов».
Модель CAPM, чаще всего, применяется для объяснения динамики курсов ценных бумаг и функционирования механизма, посредством которого инвесторы могли бы оценивать влияние инвестиций в предполагаемые ценные бумаги на риск и доходность их портфеля.
Концепция этой модели была разработана в 1950-х гг. в США Гарри Марковицем [1], дальнейшее развитие модель получила в работах Jack Treynor (1961-1962гг.), William Sharpe (1964г.), John Lintner (1965г.) и Jan Mossin (1966г.).
Суть САРМ модели заключается в следующем: предполагая существование высоколиквидного эффективного рынка финансовых активов, можно прийти к выводу о том, что величина требуемой отдачи на средства, вложенные в какой-либо актив, определяется не столько специфическим риском, присущим конкретному активу, сколько общим уровнем риска, характерным для фондового рынка.[2]
Такой вывод может показаться противоречащим здравому смыслу – инвестору должен быть компенсирован тот риск, который он принимает, вкладывая ресурсы в капитал компании. Логика модели базируется на том, что инвестор диверсифицирует свои вложения и, хотя для разных вложений, входящих в портфель активов инвестора, характерен разный профиль риска, зачастую потери от одного актива могут быть компенсированы доходами по другому активу, что существенным образом снижает реальный уровень риска, принимаемого на себя инвестором.
Математически формула определения ожидаемой ставки доходности на долгосрочный актив имеет следующий вид:
где,
Rf — доходность безрисковых активов, под которой, как правило, понимают доходность государственных ценных бумаг;
Rm — ожидаемая средняя норма прибыли рыночного портфеля;
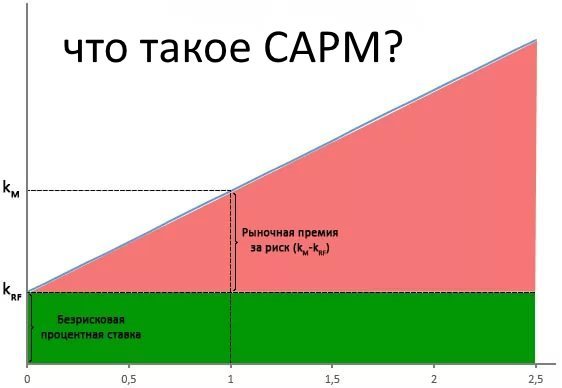
(Rm-Rf) — премия за риск вложения в акции (в ряде учебных пособий премия за рыночный риск принимается равной 5%);
β — коэффициент, характеризующий чувствительность оцениваемой ценной бумаги к изменениям рыночной доходности (рассчитывается по статистическим данным и выражает вариабельность доходности ценной бумаги по отношению к среднерыночной доходности).
Смысл модели CAPM заключается в том, что требуемая (рыночная) доходность собственного капитала есть безрисковая ставка доходности, увеличенная на риски, соответствующие акционерному капиталу.
Применительно к российской практике можно говорить о двух подходах для расчета по модели CAPM для компаний из развивающихся рынков.
Подходы к расчету модели CAPM:
Страновой риск корректируется на β-коэффициент
Страновой риск не корректируется на β-коэффициент
Если страновой риск корректируется на β-коэффициент, формула для CAPM принимает следующий вид:
В случае, когда страновой риск не корректируется на β-коэффициент, формула для CAPM принимает следующий вид:
Для непубличных компаний вышеприведенные формулы CAPM для расчета ставки дисконтирования могут дополняться показателями S1 и S2 — премиями за малый размер и специфические риски соответственно.
где,
S1 — дополнительная норма дохода за риск инвестирования в конкретную компанию;
S2 — дополнительная норма дохода за риск инвестирования в малую компанию.
Говоря о безрисковой ставке, следует пояснить, что различают несколько безрисковых ставок: глобальную безрисковую ставку и локальную безрисковую ставку.
Глобальная безрисковая ставка – ставка по государственным облигациям США, Англии, Германии и Швейцарии. (Информацию по американским государственным облигациям можно найти тут). В качестве глобальной безрисковой ставки доходности правильнее выбирать ставку доходности по 10-летним американским государственным облигациям.
Локальная безрисковая ставка – ставка по российским государственным облигациям номинированным в рублях (данные о ставке можно посмотреть здесь).
Среднерыночная доходность (Rm) представляет собой доходность рыночного портфеля. В качестве данного показателя берут, например, среднюю доходность по акциям, включенным в рыночный портфель, используемый для расчета какого-либо общеизвестного индекса (Индекс ММВБ, Nikkei 225 и т.п.), данные значения легко можно найти в открытом доступе.
Безрисковая доходность (Rf) представляет собой, ожидаемый среднегодовой темп прироста экономики в долгосрочной перспективе, но с поправкой на изменение краткосрочной ликвидности и инфляцию. Единого мнения в отношении значения показателя нет. Так, американские финансовые аналитики полагают, что в качестве доходности безрисковых активов следует брать доходность по казначейским обязательствам, но вот какие обязательства использовать долго- или краткосрочные, – единства нет.
Разницу между среднерыночной нормой доходности акций и безрисковой ставкой (Rм — Rf) называют премией за риск вложения в акции (equity risk premium, ERP).
Размер премии за риск инвестирования в акционерный капитал, ERP. В качестве ERP можно взять готовую цифру из верифицированного источника аналитических данных. К примеру для России, на 01.01.2015 ERP составлял 13,72%, а для западных компаний обычно эта премия варьируется в диапазоне 3,5% — 6%.
Бета-коэффициент характеризует чувствительность оцениваемой ценной бумаги к изменениям рыночной доходности (рассчитывается по статистическим данным и выражает вариабельность доходности ценной бумаги по отношению к среднерыночной доходности – доходности того или иного фондового индекса).
β-коэффициент выражает меру систематического риска для акций компании. Величина коэффициента определяется на основе анализа ретроспективных данных соответствующими статистическими службами фирм, специализирующихся на рынке информационно-аналитических услуг, инвестиционными и консалтинговыми компаниями и публикуется в финансовых справочниках и периодических изданиях, анализирующих фондовые рынки. Общий алгоритм расчета показателя в следующей таблице:
Общий алгоритм расчета показателя
| № п/п | Локальный β (долл.) | Локальный β (руб.) |
|---|---|---|
| 1 | Стандартное отклонение доходности RTSI | Стандартное отклонение доходности ММВБ |
| 2 | Стандартное отклонение доходности конкретного эмитента | Стандартное отклонение доходности конкретного эмитента |
| 3 | Корреляция доходностей RTSI и акций конкретного эмитента | Корреляция доходностей ММВБ и акций конкретного эмитента |
| 4 | Бета-коэффициент = стр. 2 x стр. 3 / стр. 1 | |
Отметим, информацию о бета-коэффициенте публичных компаний можно взять в виде готовой цифры из открытых источников, к примеру, для акций ГМК «Норильский никель» на 25.12.15 значение коэффициента равно 0,88.
Если необходимо рассчитать значение бета-коэффициента для непубличной компании, то можно воспользоваться формулой Хамады [6]:
Рассмотрим пример расчета бета-коэффициента для непубличной компании, занимающейся производством пищевых продуктов (скачать).
Известны достаточно простые алгоритмы, позволяющие найти приблизительное значение бета-коэффициента для данной ценной бумаги. Пусть Kij — доходность акций i-й компании в j-м году, a Kmj — доходность на рынке в среднем (j = 1, 2, . n) за все анализируемые периоды. Если к рынку применима модель САРМ, то, как следует из модели, β-коэффициент представляет собой коэффициент эластичности, а его значение можно рассчитать как отношение приращения доходности акций i-й компании (ΔKij) к приращению среднерыночной доходности (ΔKmj):
Алгоритм, задаваемый формулой, весьма приблизителен, поскольку приращения можно считать различными способами. Достаточно часто используется следующий вариант расчета β:
- определяются средние (например, по годам) значения доходности акций данной компании и по рынку в целом;
- строится уравнение линейной регрессии, отражающее зависимость средней доходности акций данной компании от доходности на рынке в среднем;
- коэффициент регрессии (т.е. коэффициент при параметре Km) и будет бета-коэффициентом.
Так как данные для расчета CAPM базируются на процентных ставках номинированных в долларах США, то при использовании рублевых денежных потоков необходимо скорректировать полученную величину ставки дисконтирования по следующей формуле:
где,
Rrur — ставка дисконтирования, номинированная в рублях;
Rusd — ставка дисконтирования, номинированная в долларах США;
Brur — доходность по рублевым государственным облигациям России;
Busd — доходность по еврооблигациям России, номинированным в долларах США.[4]
Одним из основных преимуществ в применении модели является то что, модель CAРM позволяет учесть влияние внешних факторов, не зависящих от хода реализации проекта, – страновые и политические риски, ставки доходности (без рисковые, отраслевые и среднерыночные). При этом, правда, следует учитывать и ее недостатки, к которым можно отнести:
- Имеет прямое отношение только к компаниям, которые являются открытыми акционерными обществами и, следовательно, их акциями торгуют на фондовых рынках.
- Вызывает затруднения при определении, какие из вложений можно считать без рисковыми, применим только к компаниям, которые располагают достаточной статистикой для расчета своего коэффициента бета или имеют возможность найти компанию-аналог, чей коэффициент бета мог бы использоваться в расчетах.
При использовании в модели информации зарубежных фондовых рынков в ставке дисконта необходимо учитывать дополнительный риск, связанный с инвестированием средств в Россию (страновой риск). Уровень риска инвестирования в конкретную страну определяется крупнейшими информационно-аналитическими и рейтинговыми агентствами.
Capital Asset Pricing Model, САРМ – центральная концепция современной финансовой экономики. Эта модель дает представление о том, какое должно быть соотношение между риском вложения в актив и доходностью этого вложения. Эта формула нашла широкое применение в теории современного инвестиционного анализа в самых различных его областях: оценки прибыльности проектов, портфельных инвестиций, оценки предприятий.
Источник
Модель ценообразования активов: теория и практика
Модель ценообразования CAPM
Математической основой инвестиционного портфеля является теория ценообразования активов (Capital Asset Pricing Model, САРМ), которая тесно связана с теорией Марковица. Если пытаться говорить простыми словами, то CAPM разделяет весь рыночный риск на две части: так называемую безрисковую составляющую и коэффициент бета.
Последний называется систематическим (недиверсифицируемым) риском и является столпом теории. Не систематический (диверсифицируемый) риск убирается в теории Марковица путем диверсификации портфеля по нескольким активам (видам активов) и рассмотрения риска портфеля в общем, а не каждого отдельного компонента. Предпосылки CAPM дают следующую формулу:
Ce = Cf + β (Cm-Cf), где
- Се — доходность выбранной акции;
- Cf — доходность безрисковых вложений;
- β — коэффициент, рассчитываемый для каждой акции;
- Cm — уровень доходности на рынке ценных бумаг
Спорным для интерпретации оказывается коэффициент Cf. При работе на американском рынке за него обычно принимается доходность казначейских облигаций за сроки от года до 10 лет. В условиях России даже государственные облигации далеко не все согласны считать безрисковыми, вспоминая ГКО; тем не менее, в качестве альтернативы можно предложить лишь ставку по депозитам Сбербанка или вовсе отказаться от данной методики.
Коэффициент бета показывает отношение доходности данного актива по отношению к доходности в среднем на рынке ценных бумаг и может быть рассчитан по котировкам компании. Стоит также напомнить, что в целом по рынку коэффициент β равен единице; меньшая величина в рамках теории показывает меньший риск эмитента, чем в среднем по рынку, тогда как значение, большее 1, говорит о повышенном риске.
Коэффициент зависит от времени и принимается константой только на выбранном временном промежутке; его увеличение со временем говорит о том, что актив компании начал нести больше риска (и наоборот). Теория исходит из ликвидности всех активов, отсутствия издержек на транзакции и нулевого налогообложения. Для ясности можно привести три примера.
Пример 1
Попробуем по модели CAPM вычислить справедливую доходность акции российского рынка. Возьмем в качестве безрисковой составляющей актуальную ставку Сбербанка — для вклада «Сохраняй» сроком в 1-2 года на сегодняшний день она равна 6.1%. Средняя геометрическая доходность индекса ММВБ с сентября 1997 года по июнь 2016 равна 17% годовых.
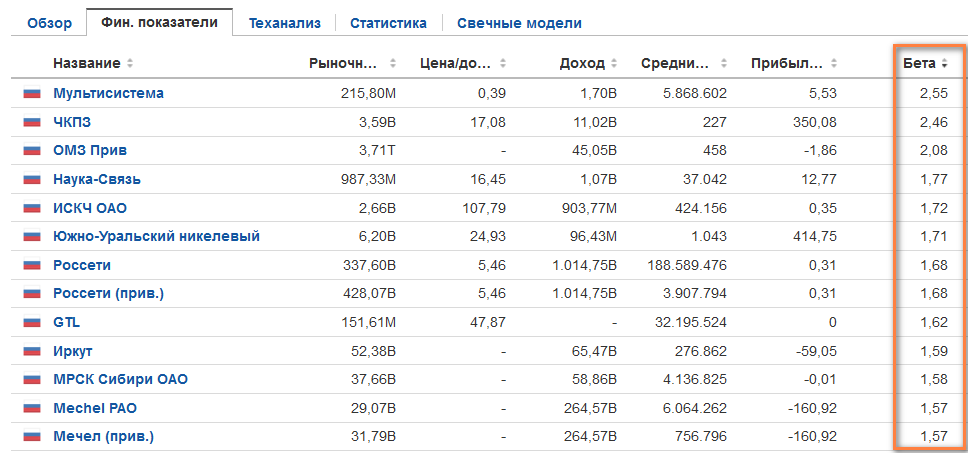
Теперь выберем какую-либо компанию Х и поищем в ее описании бета-коэффициент, который считается по двум массивам данных: доходности акции и индекса сравнения. Если коэффициент не указан, то можно рассчитать его самому . Получить котировки российских акций можно на сайте finam.ru в разделе «Про рынок» → «Экспорт данных».
Более простой вариант это воспользоваться ссылкой https://ru.investing.com/stock-screener/ или сервисом Finviz для акций США. В первом случае коэффициент бета отображается за годовой период:
Допустим, что у нас β = 0.5. Тогда
Ce = Cf + β (Cm-Cf) = 6.1 + 0.5 (17 — 6.1) = 11.55%
Разницу между Ce и Cf можно считать компенсацией риска (премией за рыночный риск). Мы получили конкретную доходность — она ниже среднерыночной, но при этом достигнута с риском в два раза меньшим, чем у индекса. Инвестор вправе решать, включать ли акцию с таким ожидаемым доходом в свой портфель.
Пример 2
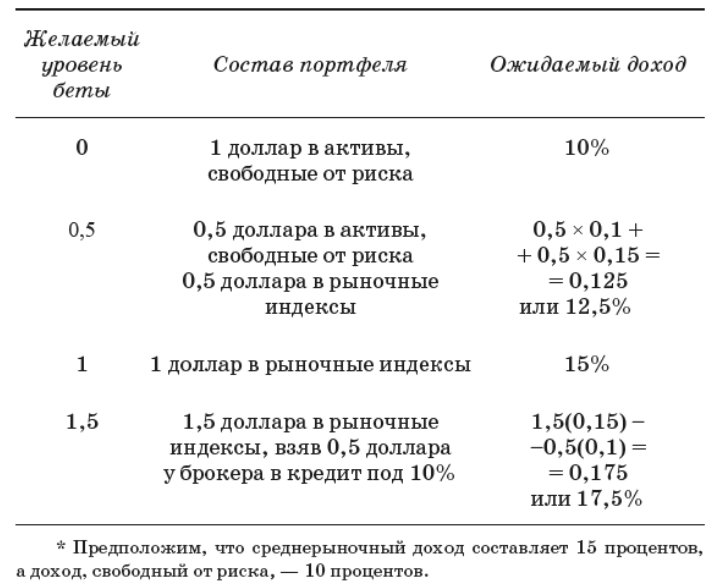
Даны две компании. Пусть компания А имеет β = 1.6, а у компании В коэффициент β = 0.9. Возьмем безрисковую ставку на уровне 6%, а среднюю доходность на рынке ценных бумаг снова 17%. Тогда
Для компании А: Се = 6 + 1,6 × (17-6) = 23,6%
Для компании В: Се = 6 + 0,9 × (17-6) = 15,9%
Расчет очевидным образом дает более высокие значения прибыли для той компании, коэффициент бета которой больше. Но значит ли это, что инвестирование в первую компанию непременно даст более высокую доходность? Нет, поскольку модель подходит к компании по принципу «черного ящика» — через коэффициент бета она учитывает историю доходности компании, но ничего не говорит о текущей и будущей ситуации в ней.
Следовательно, для принятия инвестиционного решения можно дополнительно воспользоваться фундаментальным анализом — сравнив, например, такие показатели как P/E, PEG Ratio, чистую маржу, коэффициент рентабельности активов и др. исследуемой компании с другими подобными ей или со средними значениями по отрасли. Тем не менее и это может не принести результат.
Модель исходит из линейной корреляции доходности и риска при одновременной оценке портфеля из нескольких компаний, что проще всего показать следующим расчетом:
Пусть портфель включает следующие активы со средней доходностью: А (14%); В (28%); С (35%); D (13%); Е (10%). Коэффициент бета составляет соответственно: А (1,3); В (1,6); С (0,7); D (0,9); Е (1). Найти средний коэффициент бета.
Решение: β (среднее) = 0,14 × 1,3 + 0,28 × 1,6 + 0,35 × 0,7 + 0,13 × 0,9 + 0,1 × 1 = 1,092
Выводы
Несмотря на формализм, теория САРМ позволяет произвести первичную оценку как отдельной компании, так и инвестиционного портфеля. Кроме того, она вводит такое распространенное понятие, как бета-коэффициент. Его значение может сказать нам, идет ли речь о компании роста (β > 1) или о компании стоимости (β
Источник