Оценки доходности ценных бумаг шарпа

Оценка торговой стратегии с помощью коэффициента Шарпа

Большинство инвесторов оценивают эффективность торговых стратегий на финансовых рынка по эквити. Если по результатам бэктеста кривая плавно растущая, без резких просадок — торговая стратегия эффективная. Есть и другие вспомогательные параметры: процент прибыльных сделок, максимальная просадка, и т.д. Но есть в такой оценке один изъян — она не достаточно учитывает торговые риски. Другими словами, иной раз стратегия с меньшей доходностью является более привлекательной за счет уменьшенного риска. Вот именно для оценки соотношения прибыльности и риска применяется коэффициент Шарпа, в этой статье поговорим о том, что это такое и как его использовать.

1. Что такое коэффициент Шарпа
2. Практический пример расчета эффективности стратегии
3. Усовершенствованный коэффициент Шарпа

Что такое коэффициент Шарпа

Я веду этот блог уже более 6 лет. Все это время я регулярно публикую отчеты о результатах моих инвестиций. Сейчас публичный инвестпортфель составляет более 1 000 000 рублей.

Специально для читателей я разработал Курс ленивого инвестора, в котором пошагово показал, как наладить порядок в личных финансах и эффективно инвестировать свои сбережения в десятки активов. Рекомендую каждому читателю пройти, как минимум, первую неделю обучения (это бесплатно).

Чем выше прибыль при использовании торговой стратегии, тем выше риск. И в какой-то момент риск получить убыток перевешивает вероятность получения прибыли. Коэффициент Шарпа — это параметр, который показывает насколько доход от стратегии соотносится к потенциальному риску.

Расчет данного коэффициента может одинаково применяться как для оценки стратегии на форекс (ниже приведу пример), так и для оценки отдельно взятого инвестиционного портфеля (полезный коэффициент для тех, кто собирается стать инвестором ПИФов).

Формула расчета коэффициента Шарпа:

r_p — доход за фиксированный период (эти данные можно найти в статистике, например, торговой платформы Метатрейдера 4), r_f — безрисковый доход, σ_p — стандартное отклонение. На форексе стандартное отклонение определяется средней волатильностью валютной пары.

Параметр r_f Коэффициента Шарпа на форексе отсутствует (принимается за 0), на фондовом рынке в качестве значения принимается доходность, например, казначейских краткосрочных векселей. Кстати, я немного не согласен с тем, что для Форекса этот параметр отсутствует. Безрисковый доход — это минимальный доход, который инвестор мог бы получить от инвестиции с практически нулевым риском, и исключение этого параметра искусственно завышает значение коэффициента Шарпа. Я бы советовал в качестве безрискового дохода брать, например, доходность по депозитам.

Сервис копирования сделок RAMM от AMarkets

Что такое сервис RAMM и как в нём копировать сделки

Какой должен быть коэффициент Шарпа:

• «1 и выше» — оптимальное значение коэффициента, обозначающее хорошую стратегию или высокую результативность управления портфелем ценных бумаг;
• «0-1» — нельзя сказать, что стратегия очень хорошая, поскольку завышены риски, но её применение возможно;
• «0 и ниже» — на форексе стратегию лучше не использовать, при фондовом инвестировании целесообразнее выбрать другой портфель.

Практический пример расчета эффективности стратегии

Пример сравнения двух стратегий при торговле у брокера Амаркетс :

Пример 1.

• начальный депозит — 100 дол. США;
• период торговли — 1 год;
• доходность за год — 250% (250 дол. США);
• волатильность валютной пары за год (разница между начальным и конечным значением котировок) — 125 пунктов.

Коэффициент Шарпа = 250/125 = 2,0.

• начальный депозит — 500 дол. США;
• период торговли — 1 год;
• доходность — 60% (300 дол. США);
• волатильность — 1345 пунктов.

Коэффициент Шарпа = 300/1345 = 0,22.

В первом случае при такой волатильности трейдер получил слишком большой доход. Следовательно, или нужно искать подвох, или трейдеру очень повезло. Во втором случае трейдер слишком рискует. Снова акцентирую внимание на том, что оптимальным считается значение «1» с минимальными от него отклонениями.

Если с валютным рынком все относительно просто, то с фондовым — сложнее из-за большого количества ценных бумаг и инвестиционных портфелей. У трейдера есть два варианта:

• рассчитать коэффициент Шарпа в Exel. Для этого берем котировки нужных ценных бумаг, оцениваем вес их доли в портфеле ценных бумаг, рассчитываем доходность по каждой ценной бумаге (формула, например, для «Газпрома» из примера ниже — =LN (B7/B6). Следующий шаг — расчет доходности портфеля и его риска.

Как видно по результатам, коэффициент Шарпа отрицательный, значит портфель нерезультативен и доходность по безрисковому активу (в данном примере депозиты со ставкой 12%) оказалась выше.

• посмотреть коэффициент Шарпа онлайн, например, на сайте Национальной Лиги Управляющих (nlu.ru).

Сервис копирования сделок RAMM от AMarkets

Что такое сервис RAMM и как в нём копировать сделки

Усовершенствованный коэффициент Шарпа

Выше речь шла о простом коэффициенте Шарпа, а любая упрощенная формула несовершенна. Потому существующая формула была усложнена с целью сделать расчет рисков еще более точным. Сразу предупрежу: её понимание требует знаний математической статистики и рекомендуется только в случае необходимости принятия стратегически важных решений в отношении оценки портфеля ценных бумаг (к форексу данная формула не применяется). Расчет риска в формуле основывается не только на стандартном отклонении, но и на видоизмененной мере риска, позволяющей сделать оценку будущих потерь с большей реалистичностью благодаря анализу характера распределения исторической прибыльности.

Формула усовершенствованного коэффициента Шарпа:

r_p — усредненная прибыльность портфеля ценных бумаг, r_f — усредненная прибыльность безрискового актива, σ_p — стандартное математическое отклонение прибыльности портфеля ценных бумаг, S — эксцесс распределения доходности, z_c — куртозис распределения прибыльностей портфеля, К — квантиль распределения прибыли.

Всем, кому слова «куртозис» и «квантиль» ни о чем не говорят, «Добро пожаловать» в эконометрику и математическую статистику. Глубоко копать в рамках этой статьи не вижу смысла, т.к. большинству будет достаточно общей информации.

Заключение

Надеюсь, у меня получилось объяснить простым языком что это такое коэффициент Шарпа. В идеале рекомендую создать в Экселе собственную модель, построенную на основе коэффициента с учетом вашего личного риск-менеджмента. Если остались вопросы, пишите в комментариях.

Источник

Коэффициент Шарпа | Подробное руководство с примерами Excel

Определение коэффициента Шарпа

Коэффициент Шарпа — это коэффициент, разработанный Уильямом Ф. Шарпом и используемый инвесторами для получения превышения средней доходности портфеля над безрисковой нормой доходности на единицу волатильности (стандартное отклонение) портфеля.

Объяснение

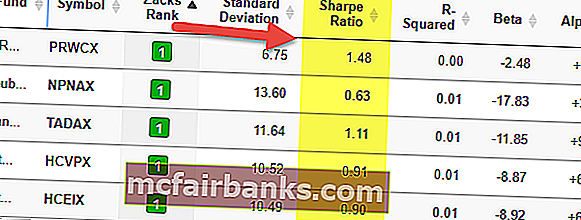
Коэффициент Шарпа — важный компонент для оценки общей доходности портфеля. Это средний доход, превышающий безрисковый доход по сравнению с общей суммой понесенного риска. Это способ оценить эффективность инвестиций с поправкой на составляющую риска. Коэффициент Шарпа характеризует, насколько хорошо доходность актива компенсирует инвестору принятый риск. При сравнении двух активов с общим эталоном, тот, который имеет более высокий коэффициент Шарпа, указывается как благоприятная инвестиционная возможность при том же уровне риска.

Если вы посмотрите на таблицу выше, вы увидите, что PRWCX имеет более высокий коэффициент Шарпа 1,48 и является лучшим фондом в своей группе.

Коэффициент Шарпа, как и любая другая математическая модель, основан на точности данных, которые должны быть правильными. При изучении инвестиционной эффективности активов со сглаживанием доходности коэффициент Шарпа будет выводиться на основе доходности базовых активов, а не доходности фонда. Этот коэффициент вместе с коэффициентами Трейнора и альфами Jeson часто используется для ранжирования эффективности различных портфелей или управляющих фондами.

Формула

В 1966 году Уильям Шарп разработал это соотношение, которое первоначально называлось отношением «вознаграждение к вариативности», прежде чем последующие ученые и финансовые операторы стали называть его коэффициентом Шарпа. Это было определено несколькими способами, пока в конечном итоге это не обозначилось как показано ниже:

Формула коэффициента Шарпа = (ожидаемая доходность — безрисковая норма доходности) / стандартное отклонение (волатильность)

Вот некоторые из концепций, которые нам необходимо понять:

• Доходность — доходность может быть различной частоты, например, ежедневно, еженедельно, ежемесячно или ежегодно, при условии нормального распределения, поскольку для получения точных результатов эти доходности можно пересчитать на год. Ненормальные ситуации, такие как более высокие пики, асимметрия распределения могут быть проблемной областью для отношения, поскольку стандартное отклонение не обладает такой же эффективностью, когда существуют эти проблемы.
• Безрисковая ставка доходности — используется для оценки того, правильно ли получает компенсация за дополнительный риск, связанный с рискованным активом. Традиционно норма доходности без финансовых потерь — это государственные ценные бумаги с самым коротким сроком действия (например, казначейский вексель США). Хотя такой вариант ценной бумаги имеет наименьшую волатильность, можно утверждать, что такие ценные бумаги должны соответствовать другим ценным бумагам эквивалентной продолжительности.
• Стандартное отклонение — это величина, которая выражает, сколько единиц из данного набора переменных отличается от среднего среднего для группы. После расчета этой избыточной доходности над безрисковой доходностью ее необходимо разделить на стандартное отклонение оцениваемого рискового актива. Чем больше это число, тем привлекательнее будут инвестиции с точки зрения соотношения риск / доход. Однако, если стандартное отклонение существенно не велико, компонент левериджа не может повлиять на коэффициент. И числитель (возврат), и знаменатель (стандартное отклонение) можно без проблем удвоить.

пример

Клиент «А» в настоящее время держит $ 450 000, вложенные в портфель с ожидаемой доходностью 12% и волатильностью 10%. Эффективный портфель имеет ожидаемую доходность 17% и волатильность 12%. Безрисковая процентная ставка составляет 5%. Что такое коэффициент Шарпа?

Формула коэффициента Шарпа = (ожидаемая доходность — безрисковая норма доходности) / стандартное отклонение (волатильность)

Коэффициент Шарпа = (0,12-0,05) / 0,10 = 70% или 0,7x

Расчет коэффициента Шарпа в Excel

Теперь, когда мы знаем, как работает формула, давайте рассчитаем коэффициент Шарпа в Excel.

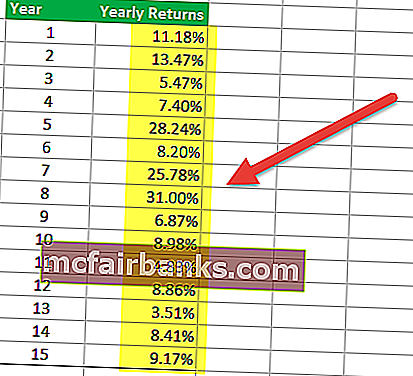
Шаг 1 — Получите доход в табличном формате

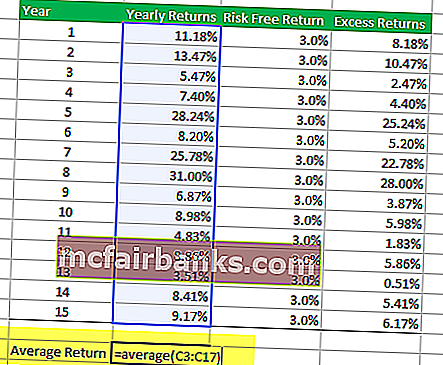
Первый шаг включает в себя организацию доходности портфеля паевого инвестиционного фонда, который вы хотите проанализировать. Временной период может быть ежемесячным, квартальным или годовым. В таблице ниже представлены годовые доходы паевого инвестиционного фонда.

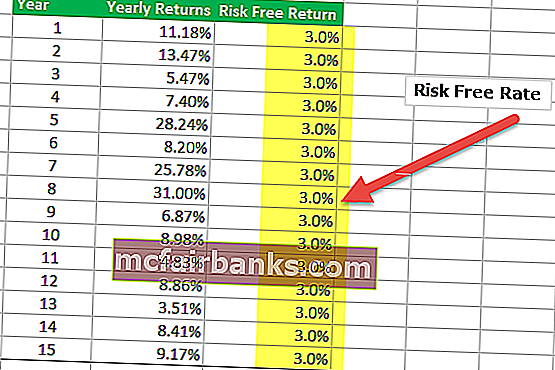
Шаг 2 — Получите подробную информацию о возврате без риска в таблице

В приведенной ниже таблице я сделал предположение, что безрисковая доходность составляет 3,0% на протяжении 15 лет. Однако безрисковая ставка может меняться каждый год, и вам необходимо указать это число здесь.

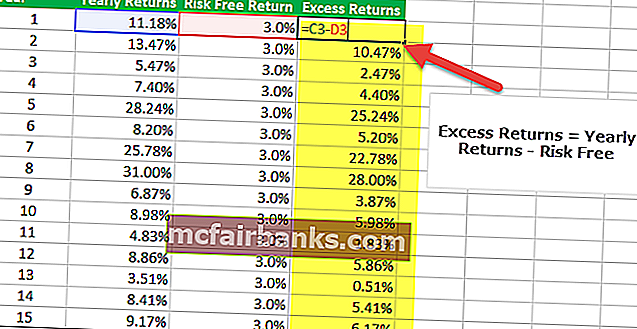
Шаг 3 — Найдите дополнительную прибыль

Третий шаг в вычислении коэффициента Шарпа в Excel — это определение избыточной доходности портфеля. В нашем случае избыточный доход — это годовой доход — безрисковый доход.

Шаг 4 — Найдите среднее значение годовой прибыли.

Четвертый шаг в вычислении коэффициента Шарпа в excel — найти среднее значение годовой доходности. Вы можете использовать формулу Excel AVERAGE, чтобы найти среднее значение портфеля. В нашем примере мы получаем среднюю доходность 12,09%.

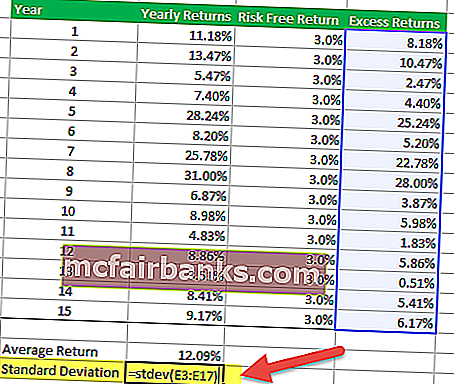
Шаг 5 — Найдите стандартное отклонение сверхдохода

Чтобы найти стандартное отклонение избыточной доходности, вы можете использовать формулу Excel STDEV, как показано ниже.

Шаг 6 — Рассчитайте коэффициент Шарпа

Последний шаг к вычислению коэффициента Шарпа в Excel — разделение средней доходности на стандартное отклонение. Получаем соотношение = 12,09% / 8,8% = 1,37x

Получаем соотношение = 12,09% / 8,8% = 1,37x

Преимущества использования коэффициента Шарпа

# 1 — Коэффициент Шарпа помогает сравнивать и противопоставлять добавление новых активов

Он используется для сравнения дисперсии общих характеристик риска и доходности портфеля всякий раз, когда к нему добавляется новый актив или класс активов.

• Например, управляющий портфелем рассматривает возможность добавления фонда сырьевых товаров к своему существующему инвестиционному портфелю 80/20, состоящему из акций с коэффициентом Шарпа 0,81.
• Если распределение нового портфеля составляет 40/40/20 акций, облигаций и распределения долгового фонда, коэффициент Шарпа увеличивается до 0,92.

Это показатель того, что, хотя вложения в фонд сырьевых товаров нестабильны как самостоятельная позиция, в данном случае они фактически приводят к улучшению характеристики доходности комбинированного портфеля и, таким образом, добавляют преимущество диверсификации в другой актив. класс к существующему портфолио. Необходимо провести тщательный анализ того, что распределение средств, возможно, придется изменить на более позднем этапе, если это окажет негативное влияние на состояние портфеля. Если добавление новой инвестиции ведет к снижению коэффициента, ее не следует включать в портфель.

# 2 — Коэффициент Шарпа помогает в сравнении риска и доходности

Этот коэффициент также может дать представление о том, является ли чрезмерная доходность портфеля результатом осторожного принятия инвестиционных решений или результатом принятых чрезмерных рисков. Хотя отдельный фонд или портфель может иметь более высокую доходность, чем его аналоги, это разумное вложение только в том случае, если такая более высокая доходность не сопряжена с чрезмерными рисками. Чем больше коэффициент Шарпа портфеля, тем лучше его результативность с учетом компонента риска. Отрицательный коэффициент Шарпа означает, что менее рискованный актив будет работать лучше, чем анализируемая ценная бумага.

Давайте возьмем пример сравнения риска и доходности.

Предположим, что портфель A имел или, как ожидается, будет иметь доходность 12% со стандартным отклонением 0,15. Предполагая, что эталонная доходность составляет около 1,5%, норма доходности (R) будет 0,12, Rf будет 0,015, а s будет 0,15. Отношение будет читаться как (0,12 — 0,015) / 0,15, что равно 0,70. Однако это число будет иметь смысл при сравнении с другим портфелем, например, портфелем «B».

Если портфель «B» показывает большую изменчивость, чем портфель «A», но имеет такую ​​же доходность, он будет иметь большее стандартное отклонение при той же норме доходности портфеля. Предполагая, что стандартное отклонение для Портфеля B составляет 0,20, уравнение будет читаться как (0,12 — 0,015) / 0,15. Коэффициент Шарпа для этого портфеля будет 0,53, что ниже по сравнению с портфелем «А». Возможно, это не удивительный результат, если учесть тот факт, что обе инвестиции приносили одинаковую прибыль, но «B» имела больший уровень риска. Очевидно, предпочтительным вариантом будет вариант с меньшим риском и той же доходностью.

Критика коэффициента Шарпа

Коэффициент Шарпа использует стандартное отклонение доходности в знаменателе в качестве альтернативы общим рискам портфеля с допущением, что доходность распределяется равномерно. Прошедшее тестирование показало, что доходность определенных финансовых активов может отклоняться от нормального распределения, что приводит к ошибочной интерпретации коэффициента Шарпа.

Это соотношение может быть улучшено различными управляющими фондами, пытающимися повысить свою очевидную доходность с поправкой на риск, что может быть выполнено следующим образом:

1. Увеличение измеряемой длительности : это приведет к меньшей вероятности волатильности. Например, среднегодовое стандартное отклонение дневной доходности обычно выше, чем еженедельной доходности, которое, в свою очередь, выше, чем у ежемесячной доходности. Чем больше продолжительность, тем четче картина, чтобы исключить любые разовые факторы, которые могут повлиять на общую производительность.
2. Составление ежемесячной доходности, но вычисление стандартного отклонения, исключая эту недавно рассчитанную совокупную ежемесячную доходность.
3. Списание решений о продаже и покупке портфеля без прибыли : такая стратегия потенциально может увеличить доходность за счет сбора премии за опционы без выплаты в течение ряда лет. Стратегии, предполагающие оспаривание риска дефолта, риска ликвидности или других форм широко распространяющихся рисков, обладают такой же способностью сообщать о смещенном в сторону повышения коэффициента Шарпа.
4. Сглаживание доходности: использование определенных производных структур, нерегулярная маркировка менее ликвидных активов на рынке или использование определенных моделей ценообразования, которые недооценивают ежемесячную прибыль или убытки, могут снизить ожидаемую волатильность.
5. Устранение экстремальной доходности: слишком высокая или слишком низкая доходность может увеличить стандартное отклонение любого портфеля, поскольку это расстояние от среднего. В таком случае управляющий фондом может решить исключать максимальные (наилучшие и наихудшие) ежемесячные доходы каждый год, чтобы уменьшить стандартное отклонение и повлиять на результаты, поскольку такая разовая ситуация может повлиять на общее среднее значение.

Коэффициент Шарпа ex-ante и ex-post

Коэффициент Шарпа пересматривался несколько раз, но использовались две общие формы: ex-ante (прогнозирование будущей доходности и дисперсии) и ex-post (анализ прошлой дисперсии доходности).

• Прогнозы ожидаемого коэффициента Шарпа позволяют легко оценить закономерности после наблюдений за прошлой эффективностью аналогичной инвестиционной деятельности.
• Коэффициент Шарпа постфактум измеряет, насколько высока была доходность по сравнению с тем, насколько разнообразной была эта доходность за определенный период времени. В частности, это отношение дифференциальной доходности (разница между доходностью инвестиций и эталонной инвестицией) по сравнению с исторической изменчивостью (стандартным отклонением) этой доходности.

Вывод

Коэффициент Шарпа — стандартный показатель эффективности портфеля. Благодаря простоте и легкости интерпретации это один из самых популярных индексов. К сожалению, большинство пользователей забывают предположения, которые приводят к неправильному результату. Вам следует рассмотреть возможность проверки распределения доходов или подтверждения результатов с помощью эквивалентных показателей эффективности, прежде чем принимать решение на рынке.

Источник