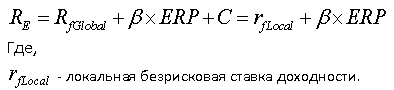Оценки доходности финансовых активов сарм capital asset pricing model

САРМ. Модель ценообразования активов (Capital Asset Pricing Model)

Распространенным подходом к оценке уровня премий за акционерный риск, применяемым на практике основными инвестбанками и аудиторами, является модель САРМ (Capital Asset Pricing Model), другое название – модель ценообразования на рынке капитальных финансовых активов, изредка в учебной литературе встречается аббревиатура МОДА, то есть «модель оценки долгосрочных активов».

Модель CAPM, чаще всего, применяется для объяснения динамики курсов ценных бумаг и функционирования механизма, посредством которого инвесторы могли бы оценивать влияние инвестиций в предполагаемые ценные бумаги на риск и доходность их портфеля.

Концепция этой модели была разработана в 1950-х гг. в США Гарри Марковицем [1], дальнейшее развитие модель получила в работах Jack Treynor (1961-1962гг.), William Sharpe (1964г.), John Lintner (1965г.) и Jan Mossin (1966г.).

Суть САРМ модели заключается в следующем: предполагая существование высоколиквидного эффективного рынка финансовых активов, можно прийти к выводу о том, что величина требуемой отдачи на средства, вложенные в какой-либо актив, определяется не столько специфическим риском, присущим конкретному активу, сколько общим уровнем риска, характерным для фондового рынка.[2]

Такой вывод может показаться противоречащим здравому смыслу – инвестору должен быть компенсирован тот риск, который он принимает, вкладывая ресурсы в капитал компании. Логика модели базируется на том, что инвестор диверсифицирует свои вложения и, хотя для разных вложений, входящих в портфель активов инвестора, характерен разный профиль риска, зачастую потери от одного актива могут быть компенсированы доходами по другому активу, что существенным образом снижает реальный уровень риска, принимаемого на себя инвестором.

Математически формула определения ожидаемой ставки доходности на долгосрочный актив имеет следующий вид:

где,
Rf — доходность безрисковых активов, под которой, как правило, понимают доходность государственных ценных бумаг;
Rm — ожидаемая средняя норма прибыли рыночного портфеля;
(Rm-Rf) — премия за риск вложения в акции (в ряде учебных пособий премия за рыночный риск принимается равной 5%);
β — коэффициент, характеризующий чувствительность оцениваемой ценной бумаги к изменениям рыночной доходности (рассчитывается по статистическим данным и выражает вариабельность доходности ценной бумаги по отношению к среднерыночной доходности).

Смысл модели CAPM заключается в том, что требуемая (рыночная) доходность собственного капитала есть безрисковая ставка доходности, увеличенная на риски, соответствующие акционерному капиталу.

Применительно к российской практике можно говорить о двух подходах для расчета по модели CAPM для компаний из развивающихся рынков.

Подходы к расчету модели CAPM:

Страновой риск корректируется на β-коэффициент

Страновой риск не корректируется на β-коэффициент

Если страновой риск корректируется на β-коэффициент, формула для CAPM принимает следующий вид:

В случае, когда страновой риск не корректируется на β-коэффициент, формула для CAPM принимает следующий вид:

Для непубличных компаний вышеприведенные формулы CAPM для расчета ставки дисконтирования могут дополняться показателями S1 и S2 — премиями за малый размер и специфические риски соответственно.

где,
S1 — дополнительная норма дохода за риск инвестирования в конкретную компанию;
S2 — дополнительная норма дохода за риск инвестирования в малую компанию.

Говоря о безрисковой ставке, следует пояснить, что различают несколько безрисковых ставок: глобальную безрисковую ставку и локальную безрисковую ставку.

Глобальная безрисковая ставка – ставка по государственным облигациям США, Англии, Германии и Швейцарии. (Информацию по американским государственным облигациям можно найти тут). В качестве глобальной безрисковой ставки доходности правильнее выбирать ставку доходности по 10-летним американским государственным облигациям.

Локальная безрисковая ставка – ставка по российским государственным облигациям номинированным в рублях (данные о ставке можно посмотреть здесь).

Среднерыночная доходность (Rm) представляет собой доходность рыночного портфеля. В качестве данного показателя берут, например, среднюю доходность по акциям, включенным в рыночный портфель, используемый для расчета какого-либо общеизвестного индекса (Индекс ММВБ, Nikkei 225 и т.п.), данные значения легко можно найти в открытом доступе.

Безрисковая доходность (Rf) представляет собой, ожидаемый среднегодовой темп прироста экономики в долгосрочной перспективе, но с поправкой на изменение краткосрочной ликвидности и инфляцию. Единого мнения в отношении значения показателя нет. Так, американские финансовые аналитики полагают, что в качестве доходности безрисковых активов следует брать доходность по казначейским обязательствам, но вот какие обязательства использовать долго- или краткосрочные, – единства нет.

Разницу между среднерыночной нормой доходности акций и безрисковой ставкой (Rм — Rf) называют премией за риск вложения в акции (equity risk premium, ERP).

Размер премии за риск инвестирования в акционерный капитал, ERP. В качестве ERP можно взять готовую цифру из верифицированного источника аналитических данных. К примеру для России, на 01.01.2015 ERP составлял 13,72%, а для западных компаний обычно эта премия варьируется в диапазоне 3,5% — 6%.

Бета-коэффициент характеризует чувствительность оцениваемой ценной бумаги к изменениям рыночной доходности (рассчитывается по статистическим данным и выражает вариабельность доходности ценной бумаги по отношению к среднерыночной доходности – доходности того или иного фондового индекса).

β-коэффициент выражает меру систематического риска для акций компании. Величина коэффициента определяется на основе анализа ретроспективных данных соответствующими статистическими службами фирм, специализирующихся на рынке информационно-аналитических услуг, инвестиционными и консалтинговыми компаниями и публикуется в финансовых справочниках и периодических изданиях, анализирующих фондовые рынки. Общий алгоритм расчета показателя в следующей таблице:

Общий алгоритм расчета показателя

№ п/п	Локальный β (долл.)	Локальный β (руб.)
1	Стандартное отклонение доходности RTSI	Стандартное отклонение доходности ММВБ
2	Стандартное отклонение доходности конкретного эмитента	Стандартное отклонение доходности конкретного эмитента
3	Корреляция доходностей RTSI и акций конкретного эмитента	Корреляция доходностей ММВБ и акций конкретного эмитента
4	Бета-коэффициент = стр. 2 x стр. 3 / стр. 1

Отметим, информацию о бета-коэффициенте публичных компаний можно взять в виде готовой цифры из открытых источников, к примеру, для акций ГМК «Норильский никель» на 25.12.15 значение коэффициента равно 0,88.

Если необходимо рассчитать значение бета-коэффициента для непубличной компании, то можно воспользоваться формулой Хамады [6]:

Рассмотрим пример расчета бета-коэффициента для непубличной компании, занимающейся производством пищевых продуктов (скачать).

Известны достаточно простые алгоритмы, позволяющие найти приблизительное значение бета-коэффициента для данной ценной бумаги. Пусть Kij — доходность акций i-й компании в j-м году, a Kmj — доходность на рынке в среднем (j = 1, 2, . n) за все анализируемые периоды. Если к рынку применима модель САРМ, то, как следует из модели, β-коэффициент представляет собой коэффициент эластичности, а его значение можно рассчитать как отношение приращения доходности акций i-й компании (ΔKij) к приращению среднерыночной доходности (ΔKmj):

Алгоритм, задаваемый формулой, весьма приблизителен, поскольку приращения можно считать различными способами. Достаточно часто используется следующий вариант расчета β:

1. определяются средние (например, по годам) значения доходности акций данной компании и по рынку в целом;
2. строится уравнение линейной регрессии, отражающее зависимость средней доходности акций данной компании от доходности на рынке в среднем;
3. коэффициент регрессии (т.е. коэффициент при параметре Km) и будет бета-коэффициентом.

Так как данные для расчета CAPM базируются на процентных ставках номинированных в долларах США, то при использовании рублевых денежных потоков необходимо скорректировать полученную величину ставки дисконтирования по следующей формуле:

где,
Rrur — ставка дисконтирования, номинированная в рублях;
Rusd — ставка дисконтирования, номинированная в долларах США;
Brur — доходность по рублевым государственным облигациям России;
Busd — доходность по еврооблигациям России, номинированным в долларах США.[4]

Одним из основных преимуществ в применении модели является то что, модель CAРM позволяет учесть влияние внешних факторов, не зависящих от хода реализации проекта, – страновые и политические риски, ставки доходности (без рисковые, отраслевые и среднерыночные). При этом, правда, следует учитывать и ее недостатки, к которым можно отнести:

1. Имеет прямое отношение только к компаниям, которые являются открытыми акционерными обществами и, следовательно, их акциями торгуют на фондовых рынках.
2. Вызывает затруднения при определении, какие из вложений можно считать без рисковыми, применим только к компаниям, которые располагают достаточной статистикой для расчета своего коэффициента бета или имеют возможность найти компанию-аналог, чей коэффициент бета мог бы использоваться в расчетах.

При использовании в модели информации зарубежных фондовых рынков в ставке дисконта необходимо учитывать дополнительный риск, связанный с инвестированием средств в Россию (страновой риск). Уровень риска инвестирования в конкретную страну определяется крупнейшими информационно-аналитическими и рейтинговыми агентствами.

Capital Asset Pricing Model, САРМ – центральная концепция современной финансовой экономики. Эта модель дает представление о том, какое должно быть соотношение между риском вложения в актив и доходностью этого вложения. Эта формула нашла широкое применение в теории современного инвестиционного анализа в самых различных его областях: оценки прибыльности проектов, портфельных инвестиций, оценки предприятий.

Источник

Модель оценки капитальных активов | Capital Asset Pricing Model, CAPM

В финансах модель оценки капитальных активов (англ. Capital Asset Pricing Model, CAPM) применяется для определения требуемой нормы доходности актива или портфеля активов. Модель CAPM учитывает систематический (недиверсифицируемый) риск, мерой которого выступает бета-коэффициент, ожидаемую рыночную доходность и безрисковую процентную ставку.

Исходные положения модели CAMP

Большинство исходных положений модели строятся исходя из гипотезы эффективности рынка.

1. Все инвесторы действуют рационально и не склонны к риску, преследуя цель максимизации своего благосостояния на конец периода (предполагается, что инвестиционный горизонт у всех инвесторов одинаковый).
2. Рынки являются совершенными: модель оценки капитальных активов не учитывает транзакционные издержки, налоги, инфляцию и существующие ограничения на короткую продажу.
3. Все инвесторы могут получать или предоставлять неограниченное финансирование по безрисковой процентной ставке.
4. Все инвесторы имеют одинаковый доступ к информации, а среднеквадратическое отклонение доходности актива является единственным показателем меры риска. Следовательно, у всех инвесторов будут одинаковые ожидания относительно доходности определенного актива.
5. Все активы бесконечно дробиться и являются абсолютно ликвидными.
6. Общее количество активов на рынке является фиксированным в пределах определенного периода времени.
7. Распределение доходности активов является нормальным или близким к нормальному.
8. Все рынки находятся в равновесии, и ни один участник самостоятельно не может повлиять на цену актива.

Формула

Модель CAMP дает возможность рассчитать ожидаемую доходность определенной ценной бумаги, для чего необходимо воспользоваться следующей формулой:

где — ожидаемая норма доходности i-ой ценной бумаги.

K_RF – безрисковая процентная ставка;

β_i – бета-коэффициент i-ой ценной бумаги;

– ожидаемая доходность рыночного портфеля.

При этом премию за риск для рыночного портфеля (RP_p) можно рассчитать следующим образом:

В свою очередь, премия за риск для i-ой ценной бумаги (RP_i) составляет:

Пример расчета

Исторические данные о доходности акций Компании XYZ и доходности рыночного портфеля представлены в таблице:

При этом безрисковая процентная ставка составляет 1,5%.

Ожидаемая доходность рыночного портфеля составит 3,208%.

= (2,25+2,43+2,74+3,21+3,05+3,27+3,59+3,86+3,67+4,01)/10 = 3,208%

Бета-коэффициент акций Компании XYZ составит 1,74, что говорит об относительно высоком риске инвестирования в эти ценные бумаги. (О том, как рассчитывается бета-коэффициент можно прочитать здесь)

Таким образом, согласно модели CAMP ожидаемая норма доходности акций Компании XYZ составит 6,98%.

= 1,5+3,208(3,208-1,5) = 6,98%

Ограничения в применении модели оценки капитальных активов

Хотя модель CAMP является достаточно простой в применении, многие ее исходные положения полностью или частично не выполняются на реальных рынках.

1. Отсутствие транзакционных издержек. Все сделки на реальных рынках предполагают наличие транзакционных издержек, причем их уровень может существенно отличаться для различных участников рынка. Например, для крупных институциональных инвесторов они будут значительно ниже, чем для мелких частных инвесторов, за счет эффекта масштаба деятельности.
2. Нулевые ставки налогообложения. Современные системы налогообложения могут быть достаточно сложными, особенно в отношении финансовых инвестиций. Налог на прирост капитала, налог на дивиденды, отложенный налог могут иметь различные ставки, что будет стимулировать инвесторов формировать свои портфели таким образом, чтобы минимизировать затраты, связанные с выплатой налогов. Все это снижает эффективность инвестиций и оказывает существенное воздействие на ценообразование активов.
3. Однородные ожидания инвесторов. Такая ситуация возможна только при наличии абсолютно эффективного рынка, что не встречается на практике. Однако следует отметить, что некоторые рынки характеризуются высокой степенью эффективности.
4. Возможность инвестирования в безрисковые активы. Наличие безрисковых ценных бумаг является одним из базовых предположений модели оценки капитальных активов. Однако на практике даже инвестиции в трежерис предполагают принятие некоторых рисков, а именно: риск инфляции, валютный риск, риск реинвестирования.
5. Возможность привлечения дополнительного финансирования под безрисковую процентную ставку. Получая дополнительное финансирование под безрисковую процентную ставку инвесторы увеличивают долю рисковых активов в своих портфелях. Однако в реальной практике стоимость привлечения финансирования для мелких инвесторов, как правило выше, чем для крупных институциональных.
6. Бета-коэффициент является полной мерой риска. Модель САРМ предполагает, что единственной мерой риска является бета-коэффициент, который характеризует волатильность доходности ценной бумаги относительно волатильности доходности рыночного портфеля. Однако на практике существует множество других видов риска, которые оказывают существенное воздействие на ценообразование активов и выбор инвесторов: риск инфляции, риск ликвидности, риск реинвестирования.
7. Распределение доходности активов является нормальным или близким к нормальному. На практике распределение доходности активов является близким к нормальному в очень редких случаях, что также оказывает влияние на выбор инвесторов при формировании портфелей.

Источник