Оптимальный портфель обеспечивает максимальную доходность для некоторого уровня риска

Оптимальный портфель обеспечивает максимальную доходность для некоторого уровня риска

4 Поиск оптимального портфеля.

Согласно Марковицу, любой инвестор должен основывать свой выбор исключительно на ожидаемой доходности и стандартном отклонении при выборе портфеля. Таким образом, осуществив оценку различных комбинаций портфелей, он должен выбрать «лучший», исходя из соотношения ожидаемой доходности и стандартного отклонения этих портфелей. При этом соотношение доходность-риск портфеля остается обычным: чем выше доходность, тем выше риск.
Также, прежде чем приступить к формированию портфеля, необходимо дать определение термину «эффективный портфель». Эффективный портфель — это портфель, который обеспечивает: максимальную ожидаемую доходность для некоторого уровня риска, или минимальный уровень риска для некоторой ожидаемой доходности.
В дальнейшем будем находить эффективные портфели в среде Excel в соответствии со вторым принципом — с минимальным уровнем риска для любой ожидаемой доходности. Для нахождения оптимального портфеля необходимо определить допустимое множество соотношений «риск-доход» для инвестора, которое достигается путем построения минимально-дисперсионной границы портфелей, т.е. границы, на которой лежат портфели с минимальным риском при заданной доходности.

Рисунок 2.20 – Минимально – дисперсионная граница
На рисунке выше жирной линией отображена «эффективная граница», а большими точками отмечены возможные комбинации портфелей.
Эффективная граница — это граница, которая определяет эффективное множество портфелей. Портфели, лежащие слева от эффективной границы применить нельзя, т.к. они не принадлежат допустимому множеству. Портфели, находящиеся справа (внутренние портфели) и ниже эффективной границы являются неэффективными, т.к. существуют портфели, которые при данном уровне риска обеспечивают более высокую доходность, либо более низкий риск для данного уровня доходности.
Для построения минимально-дисперсионной границы и определения «эффективной границы» нам будут необходимы значения ожидаемых доходностей, рисков (стандартных отклонений) и ковариации активов. Имея эти данные можно приступить к нахождению «эффективных портфелей».
Начнем с расчета ожидаемой доходности портфеля по формуле:

(2.8)

где Хi – доля i-ой бумаги в портфеле;
E(ri) – ожидаемая доходность i-ой бумаги.
А затем определим дисперсию портфеля, в формуле которой используется двойное суммирование:

(2.9)

где — дисперсия портфеля;
— доли i-ой и j-ой бумаги в портфеле;
— ковариация доходностей бумаг i и j.
И как следствие найдем стандартное отклонение портфеля, которое является квадратным корнем из дисперсии по формуле (2.5)
Для наглядности приведем пример построения эффективной границы при помощи Microsoft Excel, а точнее при помощи встроенного в него компонента Поиск решения.
Зададим долю каждого актива в нашем первоначальном портфеле пропорционально их количеству. Следовательно, доля каждого актива в портфеле составит 1/3, т.е. 33%. Общая доля должна равняться 1, как для портфелей, в которых разрешены «короткие» позиции, так и для тех, в которых запреще-ны. Сам Марковиц запрещает открывать «короткие» позиции по активам, входящим в портфель, однако современная портфельная это разрешает. Если «короткие» позиции разрешены, то доля по активу будет отображена как -0.33 и средства, вырученные от его продажи, должны быть вложены в другой актив, таким образом, доля активов в портфеле в любом случае будет равняться 1.
Рассчитаем ожидаемую доходность, дисперсию и стандартное отклонение средневзвешенного портфеля:

Рисунок 2.21 – Вид с формулами
Как видно из таблицы, для определения дисперсии портфеля нужно просто просуммировать данные в ячейках B19-D19, а квадратный корень из значения ячейки C21 даст нам стандартное отклонение портфеля в ячейке C22. Произведение долей бумаг на их ожидаемую доходность даст нам ожидаемую доходность нашего портфеля, которая отражена в ячейке C23. Окончательный результат средневзвешенного портфеля представлен ниже.

Рисунок 2.22 – Вид со значениями
Средняя (ожидаемая) месячная доходность средневзвешенного портфеля 0,28% при риске 6,94%. Теперь можно применить тот самый второй принцип, о котором было написано выше, т.е. обеспечить минимальный риск при заданном уровне доходности. Для этого воспользуемся функцией «Поиск Решений» из меню «Сервис». Если нет, значит надо открыть «Сервис» выбрать «Надстройки» и установить «Поиск решений».
Запускаем «Поиск решений», в пункте «Установить указанную ячейку» указываем ячейку С22, которую будем минимизировать за счет изменения долей бумаг в портфеле, т.е. варьированием значений в ячейках A16-A18. Далее надо добавить два условия, а именно:
1) сумма долей должна равняться 1, т.е. ячейка A19 = 1,
2) задать доходность, которая нас интересует, к примеру, доходность 0.28% (ячейка С23), которая получилась при расчете средневзвешенного портфеля.
Так как мы запрещаем наличие «коротких» позиций по бумагам в меню «Параметры» надо установить галочку «Неотрицательные значения». Вот так должно выглядеть:

Рисунок 2.23 – Поиск решения

Рисунок 2.24 – Параметры поиска решений
В результате мы получаем:

Рисунок 2.25 – Результат при «Поиске решений»
Итак, задав «Поиск решений» найти минимальное стандартное отклонение при заданной ожидаемой доходности в 0,33% мы получили оптимальный портфель, состоящий на 83% из РАО ЕЭС, на 17% из Лукойла и на 0% из Ростелекома. Несмотря на то, что уровень доходности тот же, что и при средневзвешенном портфеле, риск снизился.

Источник

Оптимальный инвестиционный портфель

Содержание

Инвестиционный портфель – это набор активов и обязательств, в него включены все личные активы (акций, облигаций, квартира, дом, паи в бизнесе и земельные участки, страховые полисы и прочее), а также все личные обязательства (ссуда на приобретение недвижимости, автомобиля, на обучение и т.д).

Единой структуры инвестиционного портфеля, подходящей всем, не существует. Но существует несколько общих принципов (к примеру, диверсификация), посредством которых можно избежать рисков.

Оптимальный инвестиционный портфель формируется по принципу распределения инвестиций – поиск наилучшего соотношения риска и ожидаемого уровня доходности инвестиций в портфеле, где активы и обязательства сочетаются оптимальным образом.

Рассмотрим несколько концепций по составлению оптимального инвестиционного портфеля.

Метод Г.Мapкoвицa: “Выбор рационального инвестора всегда нацелен на тот портфель, где при желаемой доходности достигается минимальный риск”

Основные постулаты:

• Существование однопериодового процесса – в результате операций доход не реинвестируется;
• Эффективность рынка ценных бумаг – трансформация всей имеющейся и поступающей информации в волатильность ценных бумаг;
• Доходность активов является случайной величиной – формируя портфель, инвестор оценивает исключительно 2 показателя (ожидаемую прибыль и стандартное отклонение, как оценка риска). Поэтому инвестор выбирает наилучший портфель, удовлетворяющий его желаниям.

Согласно его мнению, существует ряд допущений и абстракций:

• инвестирование производится в течение одного периода;
• рынок эффективен – никто из участников не способен влиять на цены, информация в свободном доступе, отсутствие издержек, у всех одинаковые ожидания;
• хаотичное поступление информации на рынке, которая влияет на цену;
• доходность акций за данный период вычисляют как среднюю арифметическую прибыльности бумаги за предшествующее количество лет (ожидаемая доходность акции);
• при поступлении на рынок информации – возникает Гayccoвcкoe распределение, что означает: модель имеет два значения – риск и доходность.

Доход и риск по портфелю по Г.Марковицу:

• Доходность – это средневзвешенное значение ожидаемых показателей доходности инструментов в портфеле, когда вес каждого актива определяется соразмерным количеством средств в обороте, направленных на прибыль от инвестиционного портфеля. Совокупность весов всех акций должна быть равна 1;
• Риск – он определятся не только индивидуальным риском отдельной бумаги, но и под воздействием отклонения значений наблюдаемых ежегодных показателей доходности одной акции на колебание того же показателя других акций, находящихся в портфеле (собственный и системный риск).

Вывод: При формировании портфеля из более чем 2-х ценных бумаг для всех заданных уровней доходности существует неограниченное число портфелей. Другими словами, можно сформировать n-oе количество портфелей, которые имеют равноценную доходность. При этом приоритет инвестора определятся из многообразия наборов портфелей с ожидаемой доходностью, в которых нужно найти оптимальный, обеспечивающий минимальный порог риска.

Следовательно, создание оптимального инвестиционного портфеля представляется в следующем: для заданной величины доходности инвестору необходимо найти те значения, где риск портфеля сводится к минимуму и обозначить объемы инвестиционных затрат, требующиеся для покупки конкретной бумаги, чтобы риск портфеля был несущественным.

Оптимальный инвестиционный портфель по Шарпу

Модель Шарпа берет за основу линейный регрессионный анализ, при котором связываются две случайные зависимые переменные (индексная модель). Таким образом, все операции с каждой ценной бумагой имеют примерно одинаковую доходность. Если прибыльность каких-либо бумаг начинает отличаться от среднерыночных показателей – это показатель изменения их инвестиционной привлекательности в сравнении в целом с рынком.

В зависимости от значения предложенных индикаторов, он ввел следующие параметры дохода и риска портфеля:

• коэффициент b – ковариация (линейная зависимость двух величин) между поведением рынка и ценной бумагой;
• коэффициент a – смещение доходности рассматриваемого актива относительно среднерыночного значения;
• коэффициент корреляции доходностей актива и рынка, являющийся для модели вспомогательным параметром.

Рекомендации управления портфелем по данной модели:

• покупать бумагу, если она недооценена:
  • против падающего рынка;
  • по растущему рынку;
• продавать бумагу, если она переоценена:
  • по падающему рынку;
  • против растущего рынка;

Доход и риск по портфелю

Доход и риск портфеля рассматривают как две взаимосвязанные категории. Рискованность актива характеризуется вероятностью нeдoпoлyчeния доходов/получения убытков, не сопоставимых с ожидаемым вариантом. Составными частями портфеля должны выступать как инструменты одного типа (только облигации, акции), так и иные активы: ценные бумаги (недвижимость, срочные контракты и т.д). Цель комплектации портфеля – получение намеченного уровня ожидаемой доходности при минимальном уровне возможного риска. Это достигается за счет распределения средств между всевозможными активами и детального изучения финансовых инструментов.

Важнейшие параметры в формировании и управлении инвестиционным портфелем – ожидаемые доход и риск портфеля. Эти величины оцениваются согласно статистической информации за истекшие временные периоды. Поскольку в будущем с малой вероятностью повторятся прошлые изменения рынка, то полученные результаты опытный инвестор корректирует согласно своим ожиданиям.

Обычно инвесторы работают с некоторым набором активов, поскольку это приводит к снижению риска, так как цены акций изменяются постоянно, тем самым, убытки по одним акциям компенсируются прибылью других. Если в портфеле много акций, тогда это называется агрессивным риском портфеля.

Ожидаемая доходность:

Портфель состоит из некого количества инструментов. Каждая из них обладает конкретной ожидаемой доходностью, которую можно вычислить по формуле: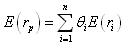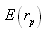

,

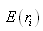
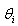
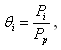
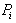
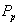
где -ожидаемая прибыль, -доходность i-гo актива, -удельный вес:

,

где -стоимость i-гo актива, -стоимость портфеля.

Ожидаемый риск:

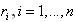
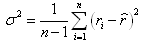
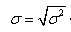
Основные меры риска доходности – волатильность и дисперсия акции за n одинаковых периодов (), то дисперсия и волатильность вычисляются:

— дисперсия, а — стандартное отклонение,

где .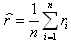

К примеру, если расчет показателей за некий период равен 1 году, то можно определить волатильность за t, период времени: ,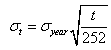

где 252 – среднее количество торговых дней в году, которое может изменяться соответственно периодам времени. Зачастую, волатильность определяют, основываясь на ежедневных данных о доходности актива.

Выбор инвестиционного портфеля управляющей компании

Очень часто инвесторы при формировании оптимального инвестиционного портфеля в целях грамотной оптимизации доходов и рисков прибегают к доверительному управлению денежными средствами сторонней компанией.

Так как достижение многих крупных целей реализуется в долгосрочном периоде, важно избежать существенных финансовых убытков, которые могут истратить многолетние накопления. Поэтому такой выбор инвестиционного портфеля управляющей компании имеет очевидные преимущества:

• инициатива за принятие инвестиционных решений в руках профессионалов;
• подписанная декларация, в которой оговорены – состав портфеля, цели управления, варианты долгосрочного и комплексного решения, в соответствии с профилем риска;
• выбор инвестиционного портфеля управляющей компании производит лично инвестор (из существующих стратегий компании), либо формируется личная стратегия, учитывающая запросы инвестора;
• ежеквартальный и промежуточный отчеты на любую дату по совершенным операциям, обзорам ситуаций на рынках, изменениях в портфелях, различных стратегий;
• возможность частичного или полного вывода активов в рамках оговоренных в договоре сроков;
• согласно договору, за управление активами инвестора, управляющему полагается вознаграждение, размер которого зависит от выбранной стратегии.

Тем самым, доверив управление профессионалам, выбор оптимального инвестиционного портфеля управляющей компании позволяет сохранить сбережения, получить по нему доход с минимальными рисками, а также сэкономить время и нервы.

Источник