Грамотное распределение инвестиций
Существуют два основных вида распределения инвестиций, о которых иногда упоминают на финансовых лекциях:
Тактическое распределение – является более продвинутым и относится к активной корректировке пропорций классов активов на основе импульса или ожидаемой доходности от этих классов активов.
Стратегическое распределение – означает владение пассивным диверсифицированным портфелем, а не изменение ваших распределений в зависимости от рыночных условий. Вы просто держите, добавляете деньги и регулярно восстанавливаете или корректируете баланс.
Дальше можно и не читать, если не хотите узнать подробности и понять нюансы каждого метода. А мы начнём с наиболее сложного, что бы более простой вам показался ещё удобнее
Тактическое распределение инвестиций
Тактическое распределение инвестиций – это наиболее сложный метод из всех известных, при котором вы с заданной периодичностью корректируете распределения по различным классам активов на основе того, где на данный момент, по вашему мнению, существуют хорошие соотношения риска и доходности на рынке.
Теоретически такой подход к инвестированию просто обязан приносить более высокий доход по отношению к любому другому варианту. Ведь, его преимущество заключается в том, что вы можете достаточно оперативно и существенно снизить риски и увеличить доходность. Однако, он более подвержен человеческим ошибкам, и если их будет много, это сильно уменьшит вашу доходность. И, в дополнение, – львиную долю дохода в этой стратегии забирают побочные издержки ( например, конвертация валюты или комиссии брокера ).
Например, некоторые инвесторы ( в том числе основатель Vanguard Джек Богл ) энергично снижали свою долю в американских акциях в разгар пузыря доткомов ( 2000 году ), потому что они видели, насколько сильно переоценены американские акции в то время по сравнению с облигациями.
Предоставленный график циклически скорректированного отношения цены к прибыли ( CAPE ) индекса S&P 500 хорошо показывает, насколько сильно переоценены были американские акции в тот момент.
В результате инвесторы удачно минимизировали негативное воздействие на свой портфель сильного медвежьего рынка акций, который вскоре и произошел.
Тактическое распределение инвестиций подразделяется ещё на несколько более мелких, но более точных направлений, и ниже, как пример мы решили раскрыть подробнее один из вариантов.
Распределение инвестиций на основе оценки
Говоря простым языком, – подобное распределение инвестиций заключается в том, чтобы постепенно увеличивать доли в пользу недооцененных активов и уменьшать долю переоцененных активов. Это не означает, что нужно выбирать либо только акции, либо только облигации. Достаточно лишь с выбранной для себя периодичностью корректировать их соотношение в пользу того или иного актива.
Такое распределение можно использовать не только применительно к классам активов. Его можно использовать, в том числе к подклассам и даже ещё глубже. Скажем, уменьшать долю американских акций в портфеле и параллельно увеличивать долю акций развивающихся стран или отечественного сектора. Можно уменьшать долю акций высокотехнологичного сектора в пользу более дешевых секторов экономики, или сырья. Та же схема применима к облигациям, товарам, валютам, недвижимости и другим классам и подклассам ваших инвестиций.
Безусловно, что собственные методы оценки у разных инвесторов варьируются, будут они особыми и у вас. Но обычно используют такие показатели, как циклически скорректированное отношение цены к прибыли ( CAPE ), отношение рыночной капитализации к ВВП, отношение цены к балансовой стоимости (P/B), отношение цены к продажам (P/S), дивидендная доходность, уровень долга и т.д.
Но перейдём от сложного к простому и привычному. Привычному? Сейчас поймёте почему…
Стратегическое распределение инвестиций
Очень распространённое диверсифицированное пассивное инвестирование по схеме « покупай и держи » – это самый простейший подход к созданию богатства для многих людей.
В соответствии с этой стратегией вы создаете диверсифицированный портфель из индексных фондов или ETF ( как наиболее простых инструментов для максимального охвата максимального же количества секторов экономики, подробнее, почему ETF считается наиболее удобным в плане диверсификации, я уже рассказывал ранее в этой статье ) и время от времени пересчитываете баланс.
Другими словами, когда один класс активов растет, а другой падает, вы продаете часть подорожавшего класса активов и покупаете упавший класс активов, чтобы постоянно поддерживать один и тот же баланс вашего инвестиционного портфеля.
С течением времени пропорции активов в портфеле рекомендуется менять. Молодым инвесторам, как правило, советуют, чтобы они начинали с агрессивного распределения с большим количеством акций, а затем постепенно, по мере приближения к пенсионному возрасту, уменьшали долю акций в портфеле, а долю облигаций наоборот увеличивали. Об этом варианте, я планирую рассказать в ближайшее время ( статья в разработке )
Если вы хотите начать инвестировать по этой стратегии, есть несколько вариантов.
Воспользоваться робоадвайзером – это робот-консультант который сейчас есть у любого брокера , который задаст вам ряд анкетных вопросов и уже на основе собранной анкеты составит для вас инвестиционный портфель ( учитывая ваш возраст, доход, любовь к риску и нескольких других факторов ). Этот робот помогает не только составить портфель, но может в дальнейшем им автоматически управлять без участия инвестора, забирая при этом определенную комиссию, а может просто периодически « влезать » со своими советами. В России этот способ инвестирования пока не очень развит, и на мой взгляд имеет определенные минусы – главный из которых, личное подозрение на то что робот будет пытаться подсунуть вам то, что выгодно брокеру ( например самые ликвидные акции, т.е. те, которые сам брокер быстро сможет продать в случае форс-мажора, вместо, по-настоящему достойных )
Составить портфель самостоятельно . На мой взгляд, это самый лучший способ, т.к. вы сами будете понимать, почему тот или иной актив нужен в вашем инвестиционном портфеле. Но для этого вам понадобится изучить специальную литературу, « порыться » в интернете, я, со своей стороны могу предложить почитать следующие статьи:
Для начала, этого вполне достаточно
Обратиться за услугой по составлению портфеля к финансовому консультанту . Несмотря на определенные ограничения, сейчас есть достаточное количество людей, которые готовы оказать услуги по составлению портфеля или финансового плана, естественно не бесплатно ( а это сразу достаточно существенный убыток, ещё до получения первой прибыли ). Проблема в том, что не все из них могут обладать достаточной компетенцией и будут действовать не в интересах клиента, а в интересах своей компании или, что случается чаще – в своих личных интересах. Поэтому, при таком подходе, самая сложная часть задачи сводиться к тому, чтобы найти достаточно квалифицированного и компетентного специалиста.
Наличие сбалансированного и в то же время обдуманного подхода к распределению активов в вашем портфеле – это ключевой способ добиться успеха в инвестировании. Наиболее примитивным вариантом будет сразу составить широко диверсифицированный портфель и использовать обыкновенное, так называемое, стратегическое распределение инвестиций. Другой вариант хитрее – тактическое распределение, которое теоретически дает шансы на получение повышенного дохода. Но эта стратегия способна хорошо работать только в руках опытного и умелого инвестора. А кто вам мешает, объединить оба варианта, и использовать лучшее из обоих описанных тут схем распределения инвестиций.
Источник
Оптимальное распределение инвестиций как задача динамического программирования.
Инвестор выделяет средства в размере D условных единиц, которые должны быть распределены между n-предприятиями. Каждое k-тое предприятие при инвестировании в него средств x приносит прибыль Wk (S, xk) условных единиц, k=1. n. Нужно выбрать оптимальное распределение инвестиций между предприятиями, обеспечивающее максимальную прибыль.
Выигрышем F в данной задаче является прибыль, приносимая n-предприятиями.
Построение математической модели:
1. Определение числа шагов. Число шагов n равно числу предприятий, в которые осуществляется инвестирование.
2. Определение состояний системы. Состояние системы на каждом шаге характеризуется количеством средств Sk, имеющихся в наличии перед данным шагом, 
3. Выбор шаговых управлений. Управление на k-м шаге 
4. Функция выигрыша на k-м шаге:

это прибыль, которую приносит k-тое предприятие при инвестировании в него средств 

следовательно, данная задача может быть решена методом динамического программирования.
5. Определение функции перехода в новое состояние.

Таким образом, если на k-м шаге система находилась в состоянии 

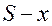



6. Составление функционального уравнения для k=n:


На последнем шаге, т.е. перед инвестированием средств в последнее предприятие, условное оптимальное управление соответствует количеству средств, имеющихся в наличии; т.е. сколько средств осталось, столько и надо вложить в последнее предприятие. Условный оптимальный выигрыш равен доходу, приносимому последним предприятием.
7. Составление основного функционального уравнения.
Подставив в формулу (53.2) выражения (53.1) и (53.3), получим следующее функциональное уравнение:

Поясним данное уравнение. Пусть перед k-м шагом у инвестора остались средства в размере 


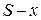




Пример: D=5000, n=3. Значения 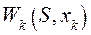

 тыс. усл. ед. тыс. усл. ед. |  тыс. усл. ед. тыс. усл. ед. |  тыс. усл.ед. тыс. усл.ед. |  тыс. усл.ед. тыс. усл.ед. |
| 1,5 | 1,7 | ||
| 2,1 | 2,4 | ||
| 2,5 | 2,3 | 2,7 | |
| 3,5 | 3,2 | ||
| 3,6 | 3,5 |
Для 

Для простоты в задаче сделано предположение, что вкладываются только тысячи условных единиц.
Проведем условную оптимизацию.
По ее результатам заполняется таблица 53.2.
| S | k=3 | k=2 | k=1 | ||
 |  |  |  |  |  |
| 1,7 | |||||
| 2,4 | 3,7 | ||||
| 2,7 | 4,4 | ||||
| 3,2 | 4,7 | ||||
| 3,5 | 1/4 | 5,2 | 6,4 |
В первой колонке таблицы записываются возможные состояния системы S=1..5, в верхней строке — номера шагов i=1..3. На каждом шаге определяются условные оптимальные управления 

· Проведение условной оптимизации для последнего шага i=3. Функциональное уравнение на последнем шаге имеет вид:

поэтому два столбца таблицы 33.2, соответствующие i=3, заполняются автоматически по таблице 33.1 исходных данных.
· Условная оптимизация для i=2. Функциональное уравнение

Для проведения условной оптимизации заполним ряд вспомогательных таблиц (таблицы 34.3—34.8), соответствующих различным значениям S, т.е. различным исходам окончания предыдущего шага.
 |  |  |  |  |
| 1,7 | 1,7 |



 |  |  |  |  |
| 2,4 | 2,4 | |||
| 1,7 | 3,7 | |||
| 2,1 | 2,1 |


 |  |  |  |  |
| 2,7 | 2,7 | |||
| 2,4 | 4,4 | |||
| 2,1 | 1,7 | 3,8 | ||
| 2,3 | 2,3 |


 |  |  |  |  |
| 3,2 | 3,2 | |||
| 2,7 | 4,7 | |||
| 2,1 | 2,4 | 4,5 | ||
| 2,3 | 1,7 | |||
| 3,5 | 3,5 |



 |  |  |  |  |
| 3,5 | 3,5 | |||
| 3,2 | 5,2 | |||
| 2,1 | 2,7 | 4,8 | ||
| 2,3 | 2,4 | 4,7 | ||
| 3,5 | 1,7 | 5,2 |
Для S=5 
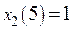

· Условная оптимизация для i=1.
Перед первым шагом состояние системы известно.
S=D=5 тыс. у.е., и условную оптимизацию следует проводить только для этого значения
S=5
 |  |  |  |  |
| 5,2 | 5,2 | |||
| 1,5 | 4,7 | 6,2 | ||
| 4,4 | 6,4 | |||
| 2,5 | 3,7 | 6,2 | ||
| 3,6 | 3,6 |



Оптимальная прибыль, приносимая тремя предприятиями при инвестировании в них 5000 у.е., равна 6,4 тыс. у.е.
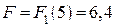
Проведем безусловную оптимизацию.
Ее результаты отмечены в таблице 34.2.
Для i=1 


Для i=2 по формуле (34.3) 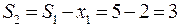


Для i=3 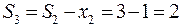



Следует пронимать, что полученное решение есть лишь некоторое приближение к оптимальному решению. Его можно улучшить, т.е. приблизить к оптимальному, взяв более мелкий шаг оптимизации, например, вкладывать в предприятия средства, кратные 500 у.е.
Теория игр. Игровые модели.
Игра – это идеализированная математическая модель коллективного поведения: несколько индивидуумов (участников, игроков) влияют на ситуацию (исход игры), причем их интересы (их выигрыши при различных возможных ситуациях) различны.
Математическая теория определяет теорию игр, как раздел математики, ориентированный на построение формальных моделей принятия оптимальных решений в ситуации конкурентного взаимодействия. Данное определение главной задачей теории игр ставит последовательность действий эффективного поведения в условиях конкуренции, конфликтности.).
В теории игр участников конкурирующего взаимодействия называют игроками, каждый из них имеет непустое множество допустимых действий, совершаемых им по ходу игры, которые называются ходами или выборами. Набор всех возможных ходов по одному из списка возможных ходов каждого игрока (участвующих в парах, тройках и т.д. ходов) называется стратегией. Грамотно построенные стратегии взаимно исключают друг друга, т.е. взаимно исчерпывают все способы поведения игроков. Исходом игры называется реализация игроком выбранной им стратегии. Каждому исходу игры соответствует определяемое игроками значение полезности (выигрыша), называемое платежом.
Классификацию игр можно проводить: по количеству игроков, количеству стратегий, характеру взаимодействия игроков, характеру выигрыша, количеству ходов, доступности информации и т.д.
1. В зависимости от количества игроков различают парные игры и игры n игроков. Математический аппарат реализации парных игр наиболее проработан. Игры трёх и более игроков исследовать сложнее из-за трудностей технической реализации алгоритмов решения.
2. По количеству стратегий игры бывают конечные и бесконечные. Конечной называется игра с конечным числом возможных стратегий игроков. Если же хотя бы один из игроков имеет бесконечное количество возможных стратегий, то игра называется бесконечной.
3. По характеру взаимодействия игры делятся на:
· бескоалиционные: игроки не имеют права вступать в соглашения, образовывать коалиции;
· коалиционные (кооперативные) – игроки могут вступать в коалиции.
В кооперативных играх коалиции жестко заданы на этапе постановки задачи и не могут меняться во время игры.
4. По характеру выигрышей игры делятся на:
· игры с нулевой суммой (общий капитал всех игроков не меняется, а перераспределяется между игроками; сумма выигрышей всех игроков равна нулю);
· игры с ненулевой суммой.
5. По виду функций выигрыша игры делятся на: матричные, биматричные, непрерывные, выпуклые, сепарабельные, дуэли и др.
Матричная игра – это конечная парная игра двух игроков с нулевой суммой, в которой задаётся выигрыш игрока 1 в виде матрицы (строка матрицы соответствует номеру применяемой стратегии игрока 2, столбец – номеру применяемой стратегии игрока 2; на пересечении строки и столбца матрицы находится выигрыш игрока 1, соответствующий применяемым стратегиям).
Для матричных игр доказано, что любая из них имеет решение и оно может быть легко найдено путём сведения игры к задаче линейного программирования.
Биматричная игра – это конечная игра двух игроков с ненулевой суммой, в которой выигрыши каждого игрока задаются матрицами отдельно для соответствующего игрока (в каждой матрице строка соответствует стратегии игрока 1, столбец – стратегии игрока 2, на пересечении строки и столбца в первой матрице находится выигрыш игрока 1, во второй матрице – выигрыш игрока 2.)
Для биматричных игр также разработана теория оптимального поведения игроков, однако решать такие игры сложнее, чем обычные матричные.
Непрерывной считается игра, в которой функция выигрышей каждого игрока является непрерывной в зависимости от стратегий. В теории математики доказано, что игры этого класса имеют решения, однако пока не разработано практически приемлемых методов их нахождения.
Целью любой игры является максимизация каждым игроком своей выгоды. Смысл математической теории игр, построенной на приведенной выше классификации, состоит в формализации (упрощении) и облегчении оптимального выбора. Множество всех возможных стратегий игр составляет большое число, растущее тем сильнее, чем больше игроков и набор доступных каждому ходов. Так для пары игроков, если условия игры позволяют каждому совершить по n ходов, в игре существует 2 n стратегий.
Простой перебор и оценка (сравнение) такого числа стратегий представляют собой технически очень сложную задачу и неприемлемы на практике. Математический аппарат позволяет значительно снизить число требующих анализа и сравнения стратегий, отбросив заведомо неэффективные. Когда же получен ограниченный, разумный для анализа набор точек равновесия (одинаково предпочитаемых всеми игроками исходов игры), на основе анализа выигрышей игроков, выбирается наиболее рациональный результат. При выборе результата существуют два основных подхода, которые дают название окончательной стратегии игры:
· Минимаксная стратегия (выбор из максимальных (наихудших) проигрышей минимальных (наилучших).
· Максиминная стратегия (выбор из минимальных (наихудших) выигрышей максимальных (наилучших).
Развитием теории игр с использованием методов вероятностного анализа является математическая теория принятия решений. Эта теория оперирует не действительным (актуальным) решением, а средним, которое есть ожидаемое решение игры в течение ее многократного повторения. Данное свойство актуально для решения правовых задач, поскольку нормативный характер права означает, что оно ориентировано на неопределенного субъекта и предполагает многократное повторение правоотношений. Чтобы не вдаваться в глубокие математические выкладки, отметим лишь, что теория принятия решений предлагает систему критериев (например, критерий Гурвица, Хаджи-Лемана, критерий ожидаемого значения), которые с помощью вероятностного анализа исходов игр позволяют осуществить выбор оптимального решения в условиях риска и неопределенности.
Источник



