Оптимальное распределение инвестиций методом динамического программирования

XI Международная студенческая научная конференция Студенческий научный форум — 2019

ОПТИМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ ИНВЕСТИЦИЙ МЕТОДАМИ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ

Для расширения четырех предприятий, принадлежащих одной организации, совет директоров выделяет средства в объеме 120 млн. руб. Зависимость прибыли предприятий от объема вложенных средств приведена в табл. 1. Определим распределение средств между предприятиями, обеспечивающее максимальную прибыль.

Шаг 1. k = 4. Предполагается, что все средства направляются на инвестирование одного предприятия (например, четвертого). Объем инвестиций для предприятия 4: . Запишем уравнение Беллмана для этого шага:

В соответствии с формулой (1) в зависимости от начальной суммы С получаем значения Z ₄ и х₄ * :

Шаг 2. k = 3. Предполагается, что все средства направляются на инвестирование двух предприятий (например, третьего и четвертого). Объем инвестиций для двух предприятий может составить: ; при этом третьему предприятию из этой суммы можно выделить любое количество . Запишем уравнение Беллмана для шага 2:

В соответствии с формулой (1.2):

Результаты расчетов на шаге 2 представлены в табл. 2.

Шаг 3. k =2. Инвестиции распределяем между тремя предприятиями (например, между вторым, третьим и четвертым). Объем инвестиций для трех предприятий может составить: ; при этом второму предприятию из этой суммы можно выделить любое количество . Запишем уравнение Беллмана для шага 3:

Найдем значения функции (1.3) для всех допустимых комбинаций С₂ и х₂:

Результаты расчетов на шаге 3 представлены в табл. 3.

Шаг 4. k =1. Инвестиции распределяем между всеми предприятиями. Между ними нужно распределить все имеющиеся денежные средства, поэтому С₁=120, при этом первому предприятию из этой суммы можно выделить любое количество: .

Уравнение Беллмана для шага 4 запишется следующим образом:

Найдем значения функции (4) для С₁ = 120:

Результаты расчетов на шаге 4 (для всех возможных значений С₁) представлены в табл. 4.

Шаг 1. По данным табл. 4 максимальная прибыль при распределении 120 млн. руб. между четырьмя предприятиями составит Z ₁=64 млн. руб., при этом первому предприятию нужно выделить млн. руб.

Шаг 2. Определим величину оставшихся денежных средств, приходящихся на долю второго, третьего и четвертого предприятий:

По данным табл. 3 находим, что при С₂ = 120: Z ₂ = 64, х₂* = 40. Это означает, что второму предприятию следует выделить 40 млн. руб.

Шаг 3. Определим величину оставшихся денежных средств, приходящихся на долю третьего и четвертого предприятий:

По данным табл. 2 находим, что при С₃ = 80: Z ₃ = 44, х₃* = 40. Это означает, что третьему предприятию следует выделить 40 млн. руб. При этом максимальная прибыль второго предприятия составит:

Шаг 4. Определим величину оставшихся денежных средств, приходящихся на долю четвертого предприятия:

Максимальная прибыль третьего предприятия составит:

а четвертого предприятия соответственно:

Оптимальная стратегия распределения инвестиций: дает возможность получить максимальную суммарную прибыль:

Таким образом, максимальная прибыль на четырех предприятиях при распределении между ними 120 млн. руб. составит 64 млн. руб. и будет получена, если первому предприятию средств не выделять, а второму, третьему и четвертому выделить по 40 млн. руб.

Вентцель, Е.С. Исследование операций: задачи, принципы, методология: учебное пособие / Е.С. Вентцель. – 5-е изд., стер. – М.: КНОРУС, 2010. – 192 с.

Давыдов, Е.Г. Элементы исследования операций: учебное пособие / Давыдов Е.Г. – М.: КНОРУС, 2010. – 160 с.

Есипов, Б.А. Методы исследования операций: учебное пособие / Б.А. Есипов. – Спб.: Издательство «Лань», 2010. – 256 с.

Костевич, Л.С. Математическое программирование: Информационные технологии оптимальных решений: учебное пособие / Л.С. Костевич. – М.: Новое знание, 2003. – 424 с.

Источник

Динамическое программирование. Задача о распределении инвестиций — видеоурок с решением задачи в Excel

>Ниже приведено условие задачи и текстовая часть решения. Закачка полного решения, файлы doc и xls в архиве zip, начнется автоматически через 10 секунд. Видеоурок по решению этих задач — внизу страницы.

Указать оптимальные размеры и потоки инвестирования, если прибыль от вложений (Х i ) в проекты (А i ) распределилась следующим образом:

Теперь для решения этой задачи воспользуемся Excel .

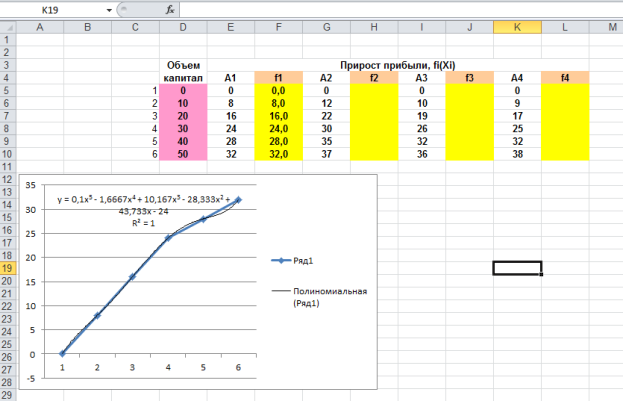
Для этого выделим шаги тренда t i , вложения x i и прибыли A i . Затем для каждого из четырех проектов построим средствами MS Excel графическую зависимость прибыли А от шага тренда ( t = 1, 2, 3, 4, 5 , 6 ). Активизируем точки графика, щелкнув по ним левой клавишей мыши, затем нажмем правую клавишу и выберем режим «Добавить линию тренда» . Для всех четырех проектов наилучшим типом является полиномиальный 5 -о й степени. С помощью полученных уравнений трендов находим теоретические значения прибыли при различных значениях шага тренда t i . Уравнения моделей тренда, коэффициенты аппроксимации и теоретические значения при были, представлены на рисунке 1.

Рис. 1. Графические зависимости прибыли от вложений и полиномиальные тренды этих зависимостей.

В ячейку М32 вводим выражение для общей (суммарной) прибыли, которую надо максимизировать, — это сумма всех четырех полиномиальных функций. Зависимыми переменными в этой функции являются искомые значения шагов тренда, которые будут располагаться в ячейках E 32 — H 32 . Суммарные вложения не должны превышать 5 0 тыс. ед., следовательно, вводим ограничение 1 0 *(E32+F32+G32 +H32 -4) в ячейку D 37 .

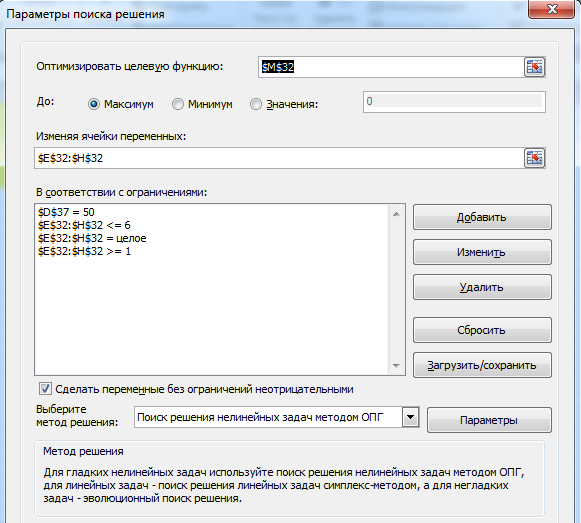
Выбираем из главного меню MS Excel режим «Поиск решения» и заполним открывшееся диалоговое окно в соответствии с требованиями. Нажмем клавишу «выполнить» и получим результат оптимизации.

Рис. 2. Модель максимизации прибыли.

Рис. 3. Оптимальное распределение капиталовложений между проектами.

Имя файла: dinprogr.zip

Размер файла: 129.98 Kb

Если закачивание файла не начнется через 10 сек, кликните по этой ссылке

Источник

Задачи динамического программирования

Данный раздел представлен следующими калькуляторами:

1. Задача распределения инвестиций. Распределении инвестиций между предприятиями П₁, П₂. П_n. Инвестируемая сумма E усл. ден. ед.
2. Задача распределения ресурсов. Планируется работа двух предприятий на n лет. Начальные ресурсы равны s₀ .
3. Метод прогонки.
4. Задача замены оборудования.
5. Складская задача: составить оптимальную программу выпуска продукции X , которая минимизирует суммарные издержки предприятия.
6. Задача Джонсона.
7. Задача о рюкзаке (решение задачи о загрузке транспортного средства).
8. Динамическая оптимизация в планировании работ
   В условиях задачи производственного планирования найти оптимальные сроки начала строительства каждого из объектов так, чтобы суммарный срок строительства всех объектов был бы минимальным.
   

   Объекты / Стадии	№1	№2	№3	№4
   A1	2	5	4	3
   A2	1	4	2	6
   A3	3	4	3	4

Задача распределения инвестиций

Таблицы могут иметь разный вид.
Таблица 1 — Первый вариант таблицы исходных данных

x	f1(x)	f2(x)	f3(x)
1	6.3	4	5
2	5.2	6	7
3	4.3	4.6	7.8
4	5	6	3
5*	7	6.3	8.2

* — здесь значение 5 — максимальное значение (сумма для распределения).

Таблица 2 — Второй вариант таблицы исходных данных

x	0	10	20	30	40
f1(x)	0	4	5	7	8
f2(x)	0	3	3	4	6
f3(x)	0	4	4	5	6

Пример задачи.
Для двух предприятий выделено A единиц средств. Как распределить все средства в течение 4 лет, чтобы доход был наибольшим, если известно, что доход от x единиц средств, вложенных в первое предприятие, равен f₁(х), а доход от y единиц средств, вложенных во второе предприятие, равен f₂(y). Остаток средств к концу года составляет g₁(x) для первого предприятия и g₂(y) для второго предприятия. Задачу решить методом динамического программирования.

При вводе данных первую нулевую строку можно не заполнять.

В сервисе Задача распределения инвестиций используется метод обратной прогонки.

Метод прогонки

В сервисе Метод прогонки необходимо также выбрать метод решения: процедура прямой или обратной прогонки.

Источник

Оптимальное распределение инвестиций методом динамического программирования

Динамическое программирование представляет собой математический аппарат, разработанный для эффективного решения некоторого класса задач математического программирования. Этот класс характеризуется возможностью естественного (а иногда и искусственного) разбиения всей операции на ряд взаимосвязанных этапов. Термин «динамическое» в названии метода возник, видимо, потому что этапы предполагаются разделенными во времени. Однако этапами могут быть элементы операции, никак не связанные друг с другом показателем времени. Тем не менее, метод решения подобных многоэтапных задач применяется один и тот же, и его название стало общепринятым, хотя в некоторых источниках его называют многоэтапным программированием.

Модели динамического программирования могут применяться, например, при разработке правил управления запасами, устанавливающими момент пополнения запасов и размер пополняющего заказа; при разработке принципов календарного планирования производства и выравнивания занятости в условиях колеблющегося спроса на продукцию; при распределении дефицитных капиталовложений между возможными новыми направлениями их использования; при составлении календарных планов текущего и капитального ремонта сложного оборудования и его замены; при разработке долгосрочных правил замены выбывающих из эксплуатации основных фондов и т.д.

Самый простой способ решения задачи – полный перебор всех вариантов. Когда количество вариантов невелико, этот способ вполне приемлем. Однако на практике задачи с небольшим числом вариантов встречаются весьма редко, поэтому полный перебор, как правило, неприемлем из-за чрезмерных затрат вычислительных ресурсов. Поэтому в таких случаях на помощь приходит динамическое программирование.

Динамическое программирование часто помогает решить задачу, переборный алгоритм для которой потребовал бы очень много времени. Этот метод использует идею пошаговой оптимизации. В этой идее есть принципиальная тонкость: каждый шаг оптимизируется не сам по себе, а с «оглядкой на будущее», на последствия принимаемого «шагового» решения. Оно должно обеспечить максимальный выигрыш не на данном конкретном шаге, а на всей совокупности шагов, входящих в операцию.

Метод динамического программирования может применяться только для определенного класса задач. Эти задачи должны удовлетворять таким требованиям:

· задача оптимизации интерпретируется как n-шаговый процесс управления;

· целевая функция равна сумме целевых функций каждого шага;

· выбор управления на k-м шаге зависит только от состояния системы к этому шагу, не влияет на предшествующие шаги (нет обратной связи);

· состояние s_k после k-го шага управления зависит только от предшествующего состояния s_k-1 и управления x_k (отсутствие последействия);

· на каждом шаге управление X_k зависит от конечного числа управляющих переменных, а состояние s_k – от конечного числа параметров.

В основе решения всех задач динамического программирования лежит «принцип оптимальности» Беллмана, который выглядит следующим образом:

каково бы ни было состояние системы S в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный.

Этот принцип впервые был сформулирован Р.Беллманом в 1953 г. Беллманом четко были сформулированы и условия, при которых принцип верен. Основное требование – процесс управления должен быть без обратной связи, т.е. управление на данном шаге не должно оказывать влияния на предшествующие шаги.

Общая постановка классической задачи распределения инвестиций.

Рассмотрим общую постановку динамической задачи распределения инвестиций.

Для развития выделены капитальные вложения в размере S. Имеется n объектов вложений, по каждому из которых известна ожидаемая прибыль fi(x), получаемая от вложения определенной суммы средств. Необходимо распределить капитальные вложения между n объектами (предприятиями, проектами) таким образом, чтобы получить максимально возможную суммарную прибыль.

Для составления математической модели исходим из предположений:

· прибыль от каждого предприятия (проекта) не зависит от вложения средств в другие предприятия;

· прибыль от каждого предприятия (проекта) выражается в одних условных единицах;

· суммарная прибыль равна сумме прибылей, полученных от каждого предприятия (проекта).

Данная постановка является упрощенной моделью реального процесса распределения инвестиций, и в «чистом» виде не встречается, так как не учитывает некоторые факторы, а именно:

· наличие «неформальных» критериев, т.е. тех, которые невозможно измерить количественно (например, согласованность проекта с общей стратегией предприятия, его социальный, либо экологический характер и т.д.), в связи с чем проекты могут иметь различный приоритет;

· уровень риска проектов;

В связи с необходимостью учета уровня риска при формировании инвестиционного портфеля появилось стохастическое динамическое программирование, которое имеет дело с вероятностными величинами. Оно нашло применение в различных областях, среди которых одной из наиболее широко исследуемых является управление рисковыми финансовыми инвестициями.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Источник