ПРИМЕНЕНИЕ ИНТЕГРАЛА В ОБЛАСТИ ФИНАНСОВ
1. Если начальный вклад составляет р, процентная ставка равна r, то
величина вклада через промежуток времени t определяется по формуле:
Рассмотрим обратную задачу для нахождения стоимости аннуитета (регулярных платежей) применительно к непрерывным процентам. В этом
случае платежи зависят от времени t, то есть является функцией от t, что
можно записать
Тогда величина вклада S через Т лет определяется формулой
Если рассмотреть понятия дисконтированной суммы, связанное для
непрерывных процентов с формулой
Эта формула дает возможности определять величину начального вклада p, если известно, что через t лет он должен составить величину S, а
непрерывная процентная ставка равна r . Задача аннуитета в этом случае
может быть сформулирована так: найти величину начального вклада p, если регулярные выплаты по этому вкладу должны составить S ежегодно в течение Т лет.
Расчетная формула имеет вид
Пример 6. Определить величину вклада через 2 года, если начальный капитал 50 000 ден. ед., процентная ставка 8%.
Решение. Используя формулу, получим общую величину вклада
через 2 года:
Пример 7. Требуется определить начальный вклад, если выплаты
должны составить 75 у.е. в течение трёх лет, а процентная ставка 5%.
Решение. Применим формулу
Пример 8. Определить дисконтированный доход за три года при процентной ставке 8%, если первоначальные (базовые) капиталовложения составили 10 тыс. условных единиц и намечается ежегодное увеличение капиталовложения на 1 тыс. у.е.
Решение. Очевидно, что капиталовложения задаются функцией

Применяя формулу интегрирования по частям, получим K=30,5 тыс. усл. единиц.
Это означает, что для получения одинаковой наращиваемой суммы через три года ежегодные капиталовложения от 10 до 13 тыс. у. е. равносильны одновременным первоначальным вложениям 30,5 тыс. у. е. при той же начисляемой непрерывно процентной ставке.
Пример 9. Определить дисконтированный доход за пять года при процентной ставке 12%, если первоначальные (базовые) капиталовложения составили 8 тыс. условных единиц и намечается ежегодное увеличение капиталовложения на 8 тыс. у.е.
В курсе микроэкономики рассматриваются так называемые предельные величины, т.е. для данной величины представляемой некоторой функцией f (x), рассматривают ее производную f’ (х). Поэтому часто приходится находить экономическую функцию (первообразную) по данной
функции предельных величин (производной).
Пример 10. Задана функция предельных издержек (издержки на производство дополнительной выпускаемой единицы продукции товара)
Найти функцию издержек С = С (q) и вычислить издержки в случае производства 15 единиц товара.
Решение. Находим интегрированием издержек на изготовление 15 ед. товара
Нахождение капитала по известным чистым инвестициям.
Чистыми инвестициями (капиталовложениями) называют общие инвестиции, производимые в экономике в течение определенного промежутка времени (чаще всего года), за вычетом инвестиций на возмещение выходящих из строя основных фондов (капитала).
Таким образом, за единицу времени капитал увеличивается на величину чистых инвестиций.
Если капитал обозначить как функцию времени K(t) ,а чистые инвестиции — I(t), сказанное выше можно записать
т.е. производная от капитала по времени t.
Часто требуется найти приращение капитала за период времени от t1 до t2 т.е. величину
Функция K(t)является первообразной для функции I(t) , поэтому можно записать:
Пример 11. Заданы чистые инвестиции функцией 
Пример 12. Задана функция чистых инвестиций 
Определить: сколько лет потребуется, чтобы приращение капитала составило 3000.
Решение. Обозначим искомый промежуток времени 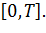
Источник
Показатели оценки инвестиционного проекта
Зачем нужен инвестпроект
Инвестиционные проект составляют, чтобы привлечь инвестиции для реализации идеи. При этом инвестиции должны быть целесообразными, иметь конкретные сроки и установленные объёмы.
Когда инвесторы рассматривают проекты, они хотят найти способ сохранить или приумножить капитал. Чтобы сделать грамотный выбор, они оценивают потенциальный доход, сроки и риски.
В статье мы разберём, какие существуют методы для оценки инвестпроектов, какие показатели рассматривают инвесторы и как их рассчитать.
Основные показатели оценки инвестпроектов
Существуют два типа современных методов оценки инвестиционных показателей: статистические и методы, основанные на дисконтировании.
Главное отличие статистических от методов дисконтирования в том, что они не учитывают временную стоимость денег.
В 1999 г. ученые Грэм и Харви попытались выяснить, какие методы используют в практике финансовые директоры американских компаний. Они отправили анкету 4440 компаниям, в которой просили указать наиболее часто используемые методы оценки проектов. Ответы были получены от 392 респондентов.
Результаты исследования показали, что крупные фирмы (с уровнем продаж до 1 млрд $) предпочитают показатели внутренней нормы доходности (IRR) и чистой дисконтированной стоимости (NPV), не всегда принимая в расчёт срок окупаемости (PBP) и дисконтированный срок окупаемости (DPP) в отличие от маленьких предприятий (с уровнем продаж до 100 млн $) [Graham, Harvey, 2001].
Источник
Расчет показателей экономической эффективности инвестиций
Задание 1. Организация планирует приобрести новое оборудование и получить разрешение на осуществление торговой деятельности, при этом первоначальные затраты оцениваются в пределах 432 тыс.руб. В течение первого года планируется дополнительно инвестировать 216 тыс.руб. (в прирост оборотного капитала и реконструкцию). Денежный поток составляет 100 тыс.руб. за год. Ликвидационная стоимость оборудования (с учетом торгового места) через 10 лет оценивается в размере 320 тыс.руб. Требуется определить экономический эффект в результате реализации данных капитальных вложений, если проектная дисконтная ставка составляет 12%.
Дисконтированные капитальные вложения определяются по формуле:
где К – суммарные капвложения,
Е – ставка дисконта;
t – год реализации проекта t=(1,n);
n – период реализации проекта.
Дисконтированный доход вычисляется по формуле
Таблица 2.11 – Денежные потоки инвестиционного проекта
| Год эксплуа-тации проекта | Инвестиционные затраты | Денежный доход | Дисконти-рующий фактор | Текущая стоимость инвестиционных затрат | Текущая стоимость денежных доходов |
| 0 | (432) | 100 | 1 | (432) | |
| 1 | (216) | 100 | 0,893 | (192,888) | 89,3 |
| 2 | 100 | 0,797 | 79,7 | ||
| 3 | 100 | 0,712 | 71,2 | ||
| 4 | 100 | 0,636 | 63,6 | ||
| 5 | 100 | 0,567 | 56,7 | ||
| 6 | 100 | 0,507 | 50,7 | ||
| 7 | 100 | 0,452 | 45,2 | ||
| 8 | 100 | 0,404 | 40,4 | ||
| 9 | 100 | 0,361 | 36,1 | ||
| 10 | 100+ 320 | 0,322 | 32,2+ 103,04 |
Сумма дисконтированных инвестиционных затрат
Σ Кд = 432+192,888=624,888 тыс. руб.
Сумма дисконтированных денежных доходов:
Σ Дд =89,3+79,7+71,2+63,6+56,7+50,7+45,2+40,4+36,1+32,2+103,04=668,14 тыс. руб.
Экономический эффект проекта
Э = — 628,344+668,14 = 39,796 ˃ 0.
Вывод: В данном случае в результате реализации проекта организация получит положительный экономический эффект. Следовательно, проект можно принять.
Задание 2. Каждый месяц вы получаете от объекта, сдаваемого в аренду, 500 долл. Эти деньги вы вкладываете в банк под 4% годовых. Сколько денег накопится на вашем банковском счете через 5 лет? Используйте технику сложного процента.
Если арендная плата, получаемая от объекта, составляет 500 долл. в месяц, соответственно за год эта плата будет составлять 6000 долл.
Накопления в банке вычисляются по формуле:
Дисконтирующий фактор при ставке дисконтирования 4% равен 0,822. Следовательно, коэффициент наращения равен 1/ 0,822 = 1,217.
Тогда количество денег в банке через 5 лет составит:
FVt = 6000·1,217 = 7302 долл.
Вывод: По истечении 5 лет вложения денег под проценты в банк, сумма вложения увеличится с 6000 долл. до 7302 долл.
Задание 3. Произведите расчет ставки дисконтирования, учитывающую инфляцию, используя модель Фишера. Безинфляционная ставка дисконта составляет 12%, среднегодовой темп инфляции – 8%.
где RN – номинальная ставка дохода (с учетом инфляции);
Rр – реальная ставка дохода (без учета инфляции);
i – коэффициент инфляции.
RN = 12 + 8 + 0,12·8 = 20,96%.
Вывод: Ставка дисконтирования, учитывающая инфляцию, составляет 20,96%.
Задание 4. Финансирование инвестиционного проекта осуществляется за счет дополнительного выпуска обыкновенных и привилегированных акций, а также за счет привлечения заемных средств. Структура капитала и цена отдельных его компонентов представлены в табл. 2.12. Требуется рассчитать среднюю взвешенную цену инвестиционного капитала.
Таблица 2.12 — Структура и цена инвестиционного капитала
| Источники финансирования | Удельный вес в общем объеме финансирования, % | Цена отдельных источников финансирования, % |
| Собственный капитал: | ||
| Обыкновенные акции | 55,0 | 25,0 |
| Привилегированные акции | 5,0 | 35,0 |
| Заемный капитал | 40,0 | 14,5 |
Средняя взвешенная цена инвестиционного капитала определяется по формуле:

где 

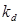



Вывод: Средняя взвешенная цена инвестиционного капитала составляет 21,3%.
Задание 5. Перед реализацией инвестиционной программы собственный и заемный капитал компании составлял соответственно 98370,0 и 25150,0 тыс. руб. Цена источников собственных средств – 15%, источников заемных средств – 8%. Оптимальная для предприятия доля заемных средств в общей величине финансирования составляет 60,0%. Для осуществления долгосрочных инвестиций необходимо дополнительно 24700,0 тыс. руб. Требуется определить предельную цену капитала, направленного на финансирование долгосрочных инвестиций, если цена собственных средств финансирования в новой структуре капитала – 15 %, цена заемных средств финансирования в новой структуре капитала – 8 %.
Сумма собственного и заемного капитала компании составит
98370 + 25150 = 123520 тыс.руб.
Доля собственных и заемных средств в общем объеме финансирования соответственно составит
Средневзвешенную цену капитала находим по формуле (2.13)
Если оптимальная для предприятия доля заемных средств составляет 60%, то от дополнительно вложенных инвестиций в размере 24700 тыс. руб это составит 14820 тыс. руб. Следовательно, доля собственных средств составит 40% или 9880 тыс. руб.
Предельная цена капитала, направленного на финансирование долгосрочных инвестиций
Вывод: Предельная цена капитала, направленного на финансирование долгосрочных инвестиций, составит 10,8%. Это ниже, чем средневзвешенная стоимость капитала до реализации инвестиционной программы (которая составляла 13,57%). Следовательно, увеличение доли заемного капиатала с 20,4% до 60% для предприятия нецелесообразно.
Задание 6. На основании данных табл. требуется рассчитать показатели дисконтированного срока окупаемости инвестиционных проектов А и В и обосновать выбор наиболее выгодного варианта капитальных вложений.
Таблица 2.13 — Начальные инвестиционные затраты и денежные потоки, тыс. руб.
| Период времени, лет | Проект А | Проект В | |||
| 0 | — 150000 | -340000 | |||
| 1 | 90000 | 98800 | |||
| 2 | 60000 | 100000 | |||
| 3 | 150000 | 90000 | |||
| 4 | — | 120000 | |||
| 0 | 1 | 2 | 3 | 4 | |
| Дисконтирующий фактор | 1 | 0,893 | 0,797 | 0,712 | 0,636 |
| Денежные потоки | (150000) | 90000 | 60000 | 150000 | — |
| Текущая стоимость | (150000) | 80370 | 47820 | 106800 | — |
| Денежные потоки | (340000) | 98800 | 100000 | 90000 | 120000 |
| Текущая стоимость | (340000) | 88228,4 | 79700 | 64080 | 76320 |
Сумма дисконтированных доходов за 1 и 2 года:
80370+47820= 128190, что меньше размера инвестиции равного 150000.
Сумма дисконтированных доходов за 1, 2 и 3 года:
128190 + 106800= =234990, что больше 150000, это значит, что возмещение первоначальных расходов произойдет раньше 3 лет.
Остаток = 1 – ((234990 — 150000)/106800) = 0,2 года.
Следовательно, дисконтированный срок окупаемости инвестиций проекта А равен 2,2 года.
Сумма дисконтированных доходов за 1 и 2 года:
88228,4+79700= 167928,4, что меньше размера инвестиции равного 340000.
Сумма дисконтированных доходов за 1, 2 и 3 года:
167928,4 + 64080=232008,4, что меньше 340000.
Сумма дисконтированных доходов за 1, 2, 3 и 4 года:
232008,4 + 76320 = 308328,4, что меньше 340000.
Следовательно, инвестиционный проект В не окупит своих капитальных вложений за 4 года, для окупаемости необходимо больше времени.
Вывод: Наиболее выгодным вариантом капитальных вложений является инвестиционный проект А, т.к. его дисконтированный срок окупаемости составляет 2,2 года, а инвестиционный проект В не окупит свои начальные инвестиционные затраты даже за 4 года.
Задание 7. На основании данных таблицы требуется рассчитать NPV к концу каждого года в течение всего срока реализации проекта и обосновать оптимальный срок реализации проекта.
Таблица 2.15 — Оценка оптимального срока реализации инвестиционного проекта
Год эксплуатации проекта
Результаты вычислений приведены в таблице 2.16
Сумма дисконтированных доходов за 1 и 2 года: 54866+48177= 103043, что больше 65780, это значит, что возмещение первоначальных расходов произойдет раньше 2 лет.
Остаток = 1 – ((103043 — 65780)/48177) = 0,23 года.
Дисконтированный срок окупаемости инвестиций равен 1,23 года.
Вывод: Оптимальным сроком реализации проекта является дисконтированный срок окупаемости проекта, который составляет 1,23 года.
Таблица 2.16 – Текущая стоимости денежных потоков и чистая текущая стоимость проекта
Год эксплуатации проекта
ЗАКЛЮЧЕНИЕ
В рамках работы над курсовой работой была достигнута поставленная цель: научная проработка проблем по оценке экономической эффективности инновационных решений и закрепление полученных знаний по технико-экономическому обоснованию инноваций в пищевой инженерии.
Инвестирование представляет собой один из наиболее важных аспектов деятельности любой динамично развивающейся организации. Для планирования и осуществления инвестиционной деятельности особую важность имеет предварительный анализ, который проводится на стадии разработки инвестиционных проектов и способствует принятию разумных и обоснованных управленческих решений. Главной задачей предварительного анализа является определение показателей возможной экономической эффективности инвестиций, т. е. отдачи от капитальных вложений, которые предусматриваются проектом, а также оценки степени риска инвестиционного проекта.
Был проведён анализ условий экономической эффективности инвестиций, который показал взаимосвязь между такими показателями как коэффициент экономической эффективности дополнительных капвложений, годовая программа, срок окупаемости, приведенные затраты, годовая экономия и годовой экономический эффект, а также произведён расчет показателей экономической эффективности инвестиций.

Последнее изменение этой страницы: 2019-03-20; Просмотров: 679; Нарушение авторского права страницы
Источник






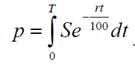



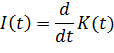

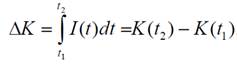




 (2.14)
(2.14)