Практическая часть. Определить эффективность инвестиций размером 200 млн
Определить эффективность инвестиций размером 200 млн. рублей, если ожидаемые ежемесячные доходы за первые 5 месяцев составят соответственно 20, 40, 60, 80 и 100 млн. рублей при годовой процентной ставке 13%.
При помощи инструмента Подбор параметра определить значение аргумента норма для эффективности 78,3.
При помощи инструмента Таблица подстановки проанализировать эффективность инвестиций для разных процентных ставок (13%, 13.5%, 14%, 14.5%, 15%) и разных значений инвестиций (170, 200, 230, 260 и 290 млн. рублей).
Представить графически влияние процентной ставки на эффективность инвестиций при заданной величине инвестиций.
Построить сценарии, используя в качестве изменяемых ячеек следующие значения инвестиций: 150, 200 и 250 млн. рублей и соответствующие им годовые процентные ставки: 20%, 15% и 10%.
Определить текущую стоимость обычных ежеквартальных платежей размером 350 тыс. рублей в течение 7 лет, если ставка процента — 11% годовых.
При помощи инструмента Подбор параметра определить значение аргумента выплата для текущей стоимости размером 6000 рублей.
При помощи инструмента Таблица подстановки проанализировать зависимость текущей стоимости платежей от годовой процентной ставки (9%, 11%, 13%, 15%, 17%, 19%) и длительности периода начисления (5, 6, 7, 8, 9, 10 лет).
Представить графически влияние значения процентной ставки на текущую стоимость платежей при заданном значении периода начисления.
Построить сценарии, используя в качестве изменяемых ячеек следующие значения платежей: 200, 300 и 400 тыс. рублей и соответствующие им годовые процентные ставки: 15%, 12,5% и 10%.
Необходимо зарезервировать деньги для специального проекта, который будет осуществлен через год. Предполагается вложить 1 млн. рублей под 60% годовых. Предполагается также вкладывать по 100 тыс. рублей в начале каждого месяца в течение 12 месяцев. Сколько денег будет на счете к концу 12-го месяца?
При помощи инструмента Подбор параметра определить значение аргумента нз для получения будущего значения размером 2,5 млн. рублей.
При помощи инструмента Таблица подстановки проанализировать зависимость значения будущей стоимости от годовой процентной ставки (9%, 11%, 13%, 15%, 17%, 19%) и начального значения вклада (1; 1,1; 1,2; 1,3 и 1,4 млн. рублей).
Представить графически влияние процентной ставки на будущее значение суммы при заданном начальном значении.
Построить сценарии, используя в качестве изменяемых ячеек следующие значения выплат: 150, 200 и 250 тыс. рублей и соответствующие им годовые процентные ставки: 40%, 30% и 20%.
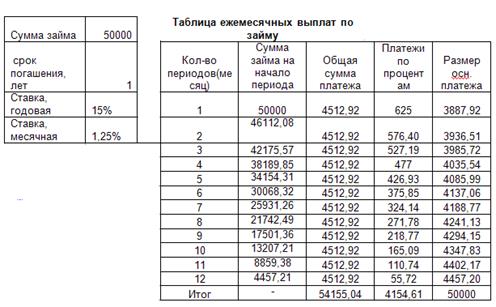
Предполагается, что ссуда размером 5000 тыс. рублей погашается ежемесячными платежами по 141,7 тыс. рублей. Рассчитать, через сколько лет произойдет погашение, если годовая ставка процента — 16%.
При помощи инструмента Подбор параметра определить значение аргумента выплата, позволяющее погасить долг за 3 года.
При помощи инструмента Таблица подстановки проанализировать зависимость срока погашения от процентной ставки (10%, 15%, 20%, 25%) и значения платежей (100, 120, 140, 160 и 180 тыс. рублей).
Представить графически влияние процентной ставки на срок погашения ссуды при заданном значении платежей.
Построить сценарии, используя в качестве изменяемых ячеек следующие значения платежей: 150, 200 и 250 тыс. рублей и соответствующие им годовые процентные ставки: 20%, 15% и 10%.
Рассчитать процентную ставку для четырехлетнего займа в 7000 тыс. рублей с ежемесячным погашением по 250 тыс. рублей при условии, что заем полностью погашается.
При помощи инструмента Подбор параметра определить значение аргумента нз, позволяющее погасить долг за эти же четыре года при годовой процентной ставке 20%.
При помощи инструмента Таблица подстановки проанализировать зависимость процентной ставки от начального значения суммы займа (5000, 6000, 7000 и 8000 тыс. рублей) и значения выплат (150, 200, 250, 300 и 400 тыс. рублей).
Представить графически влияние значения выплат на процентную ставку при заданном начальном значении займа.
Построить сценарии, используя в качестве изменяемых ячеек следующие начальные значения суммы займа: 5000, 6000 и 8000 тыс. рублей.
Облигации приобретены 06.09.03 по курсу 89 и имеют купонный доход в размере 9%, который выплачивается с периодичностью один раз в полугодие. Предполагаемая дата погашения облигации — 12.09.07 по курсу 100. Определить годовую ставку помещения. Базис расчета принять равным 1.
При помощи инструмента Подбор параметра определить значение аргумента погашение при условии годовой ставки помещения, равной 15%.
При помощи инструмента Таблица подстановки проанализировать влияние на годовую ставку помещения курса покупки облигации (79, 84, 89, 94, 99, 104, 109) и купонной ставки (5%, 10%, 15%, 20%, 25%, 30%, 35%, 40%).
Представить графически влияние значения купонной ставки на годовую ставку помещения.
Построить сценарии, используя в качестве изменяемых ячеек следующие значения аргументов ставка, цена, частота: а) 20%, 80, 4; б) 10%, 100, 2.
Литература
3. Вигдорчик Е., Нежданова Г. Элементарная математика в экономике и бизнесе. М.: Вита-Пресс, 1995.
4. Гутовская Г.В. Использование Excel для решения финансово-экономических задач / Г. В. Гутовская, Н. И. Шалагинова // Информатика и образование. – 2003. – № 3. – С. 15-21.
5. Гутовская Г.В. Использование Excel для решения финансово-экономических задач / Г.В. Гутовская, Н.И. Шалагинова // Информатика и образование. – 2003. – № 4. – С. 60-70.
6. Гутовская Г. В. Использование Excel для решения финансово-экономических задач / Г.В. Гутовская, Н.И. Шалагинова // Информатика и образование. – 2003. – № 5. – С. 54-63.
7. Едронова В.Н., Мезиковский Е.А. Учет и анализ финансовых активов: акции, облигации, векселя. М.: Финансы и статистика, 1995.
8. Компьютерные технологии обработки информации: Учеб. Пособие / Под ред. С. В. Назарова. М.: Финансы и статистика, 1995.
9. Меньшиков И.С. Финансовый анализ ценных бумаг. М., 1998.
10.Овчаренко Е.К., Ильина О. П., Балыбердин Е. В. Финансово-экономические расчеты в Excel. 2-е изд. М.: Информационно-издательский дом «Филинъ», 1998.
11.Попов А.А. Excel: практическое руководство. М. : ДЕСС КОМ, 2001.
12.Сидорчик Е., Нежданова Т. Элементарная математика в экономике и бизнесе. М.: Вита-Пресс, 1995.
13.Четыркин Е.М. Методы финансовых и коммерческих расчетов. 2-е изд. М.: Дело Лтд., 1995.
14.Экономическая информатика / Под ред. П. В. Конюховского и Д. Н. Колесникова. СПб.: Питер, 2001.
15.Экономическая информатика и вычислительная техника: Учебник / Под ред. В. П. Косарева, А. Ю. Королева. 2-е изд., перераб. и доп. М.: Финансы и статистика, 1996.
Источник
Контрольная работа: Погашение займа
| Название: Погашение займа Раздел: Рефераты по экономике Тип: контрольная работа Добавлен 04:36:59 25 июля 2010 Похожие работы Просмотров: 364 Комментариев: 15 Оценило: 3 человек Средний балл: 5 Оценка: неизвестно Скачать |
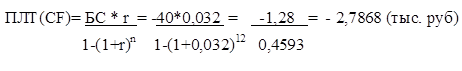
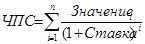
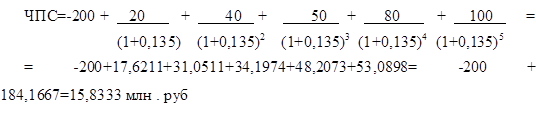

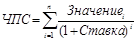
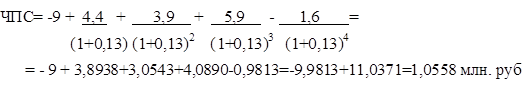
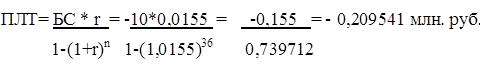
 ,
, +
+  + ….
+ ….  +… +
+… + 
 +
+  +
+  +
+  +… +
+… + 
 1 × (r2 — r1).
1 × (r2 — r1).