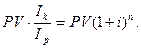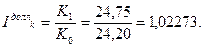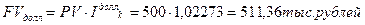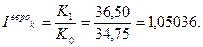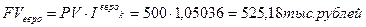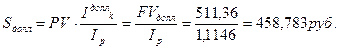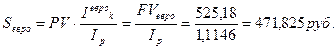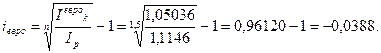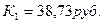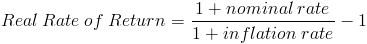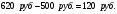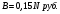Оценка доходности операции покупки валюты
Основные понятия валютных расчетов
В периоды экономической нестабильности, высокой инфляции многие граждане предпочитают хранить сбережения в свободно конвертируемой валюте (СКВ) или на валютных депозитах.
Валюта покупается и продается, как и любой другой товар, исходя из спроса и предложения. Конечная цена иностранной валюты, полученная в результате торгов, выражается в валютном курсе. Валютный курс – это цена денежной единицы национальной валюты, выраженная в денежных единицах другой страны. Установление курса иностранной валюты называется котировкой.
Различают прямую и косвенную котировку валюты, При прямой котировке курс валюты показывает, сколько единиц национальной валюты надо заплатить за одну или 100 единиц иностранной валюты. При косвенной котировке — сколько единиц иностранной валюты можно получить за одну или 100 единиц национальной валюты.
Цены продажи и покупки валюты отличаются по величине. Разница между курсом продажи и курсом покупки валюты называется спрэдом. За счет различия в курсах спроса и предложения банк имеет возможность покрыть расходы по совершению сделок, учесть возможный риск, связанный с валютными операциями, и получить определенную прибыль.
Рассмотрим, как оценивается доходность финансовой операции покупки валюты. Предположим, некоторая сумма в объеме PV рублей обменена на валюту. Затем через период n лет совершен ее обмен на рубли.
Обозначим сумму в рублях на начало операции 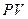
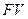
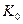
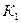
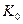
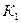
Сумма, полученная в результате проведенной операции, может быть определена по формуле:
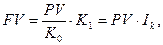
Поскольку в течение n лет в результате инфляции покупательная способность полученной суммы в определенной степени снизилась, то ее реальная покупательная способность 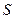
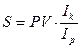
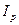
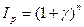
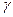
Определим доходность рассматриваемой финансовой операции в виде сложной годовой процентной ставки 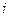
Выразив из этого равенства 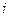
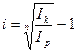
Доходность такой операции равна нулю, если выполняется условие 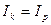
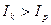
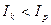
Пример. Предприниматель, имея свободную сумму 500 тыс. рублей предполагает приобрести на нее валюту с целью сохранения средств от инфляции, с тем, чтобы через 1,5 года вновь обменять валюту на рубли и приобрести на эти средства необходимое оборудование. На начало финансовой операции цена покупки доллара банком составляет 24, 15 руб., а цена продажи — 24,20 рублей. Для евро эти показатели соответственно 34, 65 руб. и 34, 75 руб. Предполагается, что концу срока цена покупки долларов банком составит 24,75 руб., а цена продажи – 24,85 руб. Аналогичные показатели для евро на конец операции – 36, 50 руб. и 36, 60 руб. Среднегодовой темп инфляции прогнозируется на уровне 7,5%.
а) сумму в рублях, полученную в результате операции покупки-продажи долларов и евро;
б) покупательную способность полученных сумм с учетом инфляции:
в) доходность финансовых операций;
г) курс покупки валюты банком в конце операции, который обеспечил бы полное сохранение средств от инфляции.
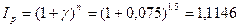
Таким образом, за 1,5 года цены возрастут на 11,46% ,
а)
Из произведенных расчетов видно, что операция с евро в данном случае дает лучший результат.
б) Скорректируем этот результат с поправкой на инфляцию:
Следовательно, не удается полностью сохранить деньги от инфляции.
в) Определим доходность рассматриваемых финансовых операций.
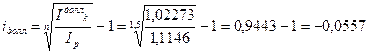
Операция с долларами является убыточной. Ее доходность отрицательна и составляет – 5,57%.
Операция с евро также убыточна. Ее доходность составляет – 3,88%.
г) Определим, при каком курсе покупки валюты в конце срока, операции по покупке-продаже валюты были бы безубыточны. Для этого используем равенство: 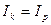
Оно выполняется в случае покупки долларов, если 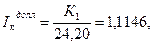
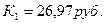
Аналогично определим критическое значение курса евро из равенства: 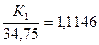
Полученный пример показывает, что достаточно сложно уберечь деньги от инфляции, не инвестируя их с целью наращения процентов.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Как правильно считать реальную доходность с учетом инфляции?
Автор: Алексей Мартынов · Опубликовано 03.07.2015 · Обновлено 02.12.2018

Чтобы хоть как-то сохранить покупательную способность своих денег, люди их вкладывают в различные финансовые инструменты: чаще всего это депозиты, валюта, недвижимость. Более продвинутые используют, акции, ПИФы, облигации, драгметаллы. С одной стороны сумма вложений растет, с другой происходит их обесценивание из-за инфляции. Если из номинальной ставки доходности вычесть ставку инфляции, получится реальная доходность. Она может быть положительной или отрицательной. Если доходность положительная, ваши вложения приумножились в реальном выражении, то есть вы можете купить больше яблок, если отрицательная — обесценились.
Большинство инвесторов считают реальную доходность по простой формуле:
Но данный способ неточен. Приведу пример: возьмем 200 рублей и положим их на депозит на 15 лет со ставкой 12% годовых. Инфляция за этот период 7% в год. Если считать реальную доходность по простой формуле, то получится 12-7=5%. Проверим этот результат, посчитав на пальцах.
За 15 лет при ставке 12% годовых 200 рублей превратятся в 200*(1+0,12)^15=1094,71. Цены за это время вырастут в (1+0,07)^15=2,76 раз. Чтобы посчитать реальную доходность в рублях делим сумму на депозите на коэффициент инфляции 1094,71/2,76=396,63. Теперь, чтобы перевести реальную доходность в проценты считаем (396,63/200)^1/15 -1 *100% = 4,67%. Это отличается от 5%, то есть проверка показывает, что расчет реальной доходности «простым» способом не точен.
Чтобы правильно рассчитать реальную доходность, нужно применять формулу:
Real Rate of Return — реальная доходность
nominal rate — номинальная ставка доходности
inflation rate — инфляция
Проверяем:
(1+0,12)/(1+0,07)-1 * 100%=4,67% Сходится, значит формула верная.
Еще одна формула, которая дает тот же результат, выглядит так:
Источник
Задачи к зачёту / РЦБ- ДОХОД И ДОХОДНОСТЬ
ДОХОД И ДОХОДНОСТЬ
Курс пакета акций из 800 штук вырос за год на 60% и составил 22 000 руб., дивиденд выплачивается раз в полугодие в размере 6 руб. на акцию. Определить полную доходность пакета акций за год.
Доход по дивидендам за год =
Начальная стоимость пакета акций = 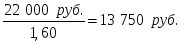
Полная доходность пакета акций

Депозитный сертификат был куплен за 20 000 руб. за восемь месяцев до его погашения и продан за 22 000 руб. за пять месяцев до погашения. Определите доходность этой операции в процентах годовых.
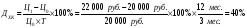
Дилер владел финансовым инструментом 18 дней и получил в этот период купонный доход 1 200 руб., рыночная цена финансового инструмента в течение периода оставалась неизменной – 14 000 руб. Определите доходность этой операции в процентах годовых.
Доходность в процентах годовых:

Курс облигации вырос за год на 20% и составил 8 000 руб., процент выплачивается раз в полугодие в размере 600 руб. Определить полную доходность облигации за год.
Начальный курс облигации = 
Процентный доход по облигации за год 
Полная доходность облигации за год:

Определите совокупный доход по акции, если известно, что акция приобретена по номинальной стоимости 500 руб. при ставке дивиденда 15% годовых. Рыночная цена акции через год после выпуска составила 620 рублей.
Совокупный доход = доход от изменения стоимости акции + дивидендный доход.
Капитализированный доход =
Дивидендный доход = 
Совокупный доход =
Какова будет доходность операции в процентах годовых, если инвестор купил по номиналу, а через два месяца продал на 15% дороже пакет облигаций с купоном 12% годовых с ежемесячной выплатой процентов по купону?
Пусть N – номинал облигации. Тогда:
Купонные платежи за период в 2 месяца = 2% от N= 0,02N
Цена продажи пакета облигаций = 1,15 N
Доходность операции в процентах за период = ((0,15N + 0,02N)/ N ) х 100% = 17%
Доходность в % годовых = (17/2) х 12 = 102%
Привилегированная акция с дивидендом 15% приобретена по цене, равной 2,75 номинальной стоимости, и продана через год за 21 000 руб., обеспечив полную доходность в 70%. Определите, за какую цену была приобретена акция.
Обозначим за N номинал акции. Тогда:
цена покупки акции 
выплата дивидендов по акции
Используя формулу доходности акции, 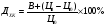
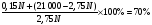
Цена покупки
Определите доходность акции в процентах, если известно, что акция приобретена по номинальной стоимости 500 руб. при ставке дивиденда 15,25% годовых. Рыночная цена акции через восемь месяцев после выпуска составила 620 рублей.
Выплата дивидендов за 8 месяцев 
Доходность 
Акция, номиналом 24 000 руб. со ставкой годового дивиденда 14% приобретена по номиналу и продана через год, обеспечив её владельцу 0,4 руб. дохода с каждого инвестируемого рубля.
Определить цену акции при продаже.
Выплата дивидендов 
За 
Используя формулу доходности акции, 


Какова будет доходность операции в процентах годовых, если инвестор купил по номиналу, а через четыре месяца продал на 18% дороже пакет акций с дивидендом 12% годовых с ежемесячной выплатой процентов?
Обозначим за N номинал акции.
Выплата дивидендов за период владения акцией 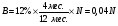
Цена продажи пакета акций 
Доходность операции в процентах годовых

Облигация номиналом 100 руб. с купонной ставкой 10% годовых и периодом обращения – 1 год имеет рыночную цену, равную 75.0. Рассчитать текущую рыночную доходность и доходность к погашению.
Текущая рыночная доходность 


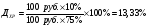
Доходность к погашению 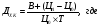



Рассчитать накопленный купонный доход по облигации с купонной ставкой 10% годовых, если с даты купонной выплаты прошло 3 месяца.
Решение: Накопленный купонный доход
Источник