Определить темпы роста инвестиций за каждый год по сравнению с предшествующим годом

Как рассчитать темп роста в процентах

tempy_rosta.jpg

Похожие публикации

Важнейшим показателем эффективности производства в анализе финансовой ситуации в компании является показатель темпа роста. Поговорим об особенностях его расчета.

Как рассчитать темп роста: формула

Этот термин показывает изменение значения любого экономического или статистического показателя в текущем периоде к его начальному значению (являющемуся базовым) за определенный временной промежуток. Измеряется он в процентах или коэффициентах.

Например, при сравнении объема выпуска товаров на конец года (допустим, в значении 100000 руб.) к показателю объема на начало года (70000 руб.) темп роста находят отношением конечного значения к начальному: 100000 / 70000 = 1,428. Индекс роста в примере составил 1,429. Это означает, что на конец года объем выпуска составил 142,9%.

Как рассчитать темп роста в процентах — формула:

ТР = П_т / П_б х 100%,

где П_к и П_б – показатели значений текущего и базового периодов.

Темп роста показывает интенсивность изменений какого-либо процесса по отношению к его начальному (базовому) значению. Результат вычислений – один из трех вариантов:

ТР больше 100%, следовательно, конечное значение возросло в сравнении с начальным, т.е. налицо рост показателя;

ТР = 100%, т.е. изменений ни в большую, ни в меньшую сторону не произошло – показатель остался на прежнем уровне;

ТР меньше 100%, значит, анализируемый показатель снизился к началу периода.

Приведем примеры, как рассчитать темп роста в процентах по каждому варианту расчета, объединив исходные данные в таблицу:

Объем выпуска в тыс. руб.

Такой темп роста называют базисным, поскольку база сравнения по периодам остается неизменной – показатель на начало периода. Если же сравнительная база изменяется, а темп роста вычисляют отношением текущего значения к предыдущему (а не базисному), то этот показатель будет цепным.

Как рассчитать цепные темпы роста

Рассмотрим пример расчета базисного и цепного темпов роста:

Период

Объем в тыс.руб.

Темп роста в %

базисный

цепной

Цепные темпы роста характеризуют насыщенность изменения уровней от квартала к кварталу, базисные же отражают ее в целом за весь временной интервал (показатель 1 квартала – база сравнения).

Сравнивая показатели в приведенном примере, можно отметить, что ряд значений, рассчитанных к началу периода, имеет меньшую амплитуду колебаний, чем цепные показатели, вычисления которых привязаны не к началу года, а к каждому предшествующему кварталу.

Как рассчитать темпы прироста

Кроме расчета темпов роста, принято высчитывать и темпы прироста. Эти значения также бывают базисными и цепными. Базисный прирост определяют как отношение разности показателей текущего и базового периодов к значению базового периода по формуле:

Цепной прирост рассчитывают как разность между текущим и предыдущим показателями, деленную на темп роста предыдущего периода:

Более простым способом расчета является формула: ∆ ТР = ТР – 100%, где расчетные показатели темпа роста уменьшаются на 100%, т. е. исходную величину. Показатель темпа прироста в отличие от значений темпа роста может иметь отрицательное значение, поскольку темп роста (или снижения) показывает динамику изменений показателя, а темп прироста говорит о том, какой характер они носят.

Продолжая пример, рассчитаем приросты объемов в рассматриваемых периодах:

Источник

Задача № 2

Качество продукции предприятия характеризуется следующими данными (за месяц):

Стоимость бракованной продукции, тыс. руб.

Определите средний процент брака в целом по предприятию.

Задача № 3

Из 200 ящиков по 100 деталей в каждом, поступивших на склад готовой продукции, в порядке случайной бесповторной выборки отобрано 5 ящиков, все детали которых проверены на вес. Результаты проверки следующие:

Средний вес 1 детали, г.

Определить: 1) возможные пределы среднего веса детали для всей партии, поступившей на склад (с вероятностью 0,954); 2) объем случайной бесповторной выборки, чтобы с вероятностью 0,683 предельная ошибка выборки при определении среднего веса одной детали для всей партии не превышала 0,7г.

Задача № 4

Известны темпы роста инвестиций за каждый год по двум регионам (в % к 2008г.):

Определить темпы роста инвестиций за каждый год по сравнению с предшествующим годом и среднегодовые темпы роста инвестиций для каждого региона. Сформулируйте вывод.

Задача № 5

Имеются следующие данные о реализации молочных продуктов на городском рынке:

Товарооборот, тыс. руб.

Изменение цены в декабре по сравнению с ноябрем, %

Рассчитайте общие индексы цен, товарооборота и физического объёма реализации.

4. Методические рекомендации по решению контрольных заданий

Данная задача решается с помощью метода группировок. Группировка – это разбиение совокупности на группы, однородные по какому – либо признаку. Этапы построения группировки:

1. Определение группировочного признака;

2. Определение числа групп;

3. Определение интервала группировки (если длина интервала не задана, то определяем его по формуле для равных интервалов: 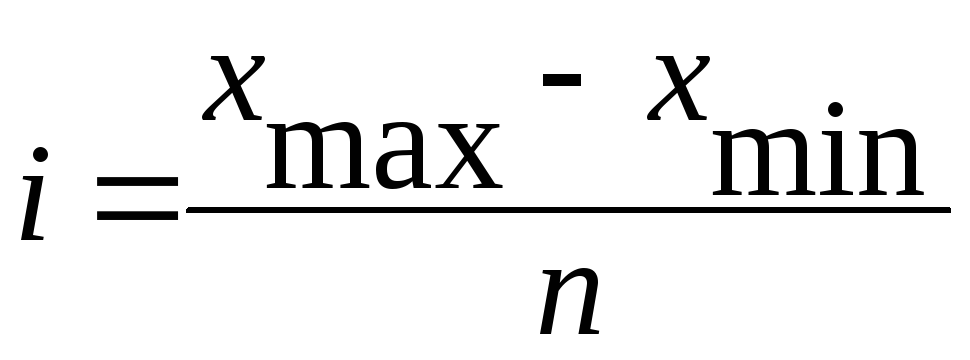, где i – длина интервала, — это максимальное, минимальное значение признака у данной единицы совокупности; n – число групп);

4. Разбиение совокупности на группы;

5. Оформление результатов в групповой таблице.

Данная задача направлена на расчет средних величин. Средней величиной в статистике называется обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину варьирующего признака в расчете на единицу качественно однородной совокупности.

Виды средних величин:

1. Средняя арифметическая простая используется, когда известны варианты (x), имеющие равновеликие частоты (n) – .

2. Средняя арифметическая взвешенная применяется, когда известны варианты, имеющие неравновеликие частоты (f) —.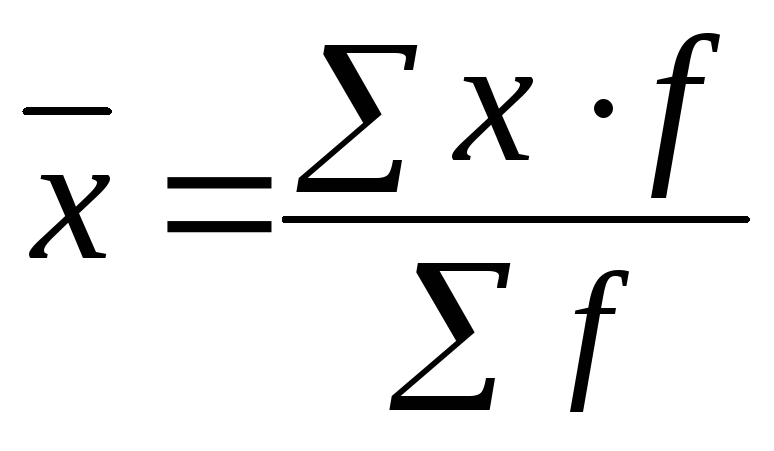

3. Средняя гармоническая простая применяется, когда вес каждого варианта равен единице — .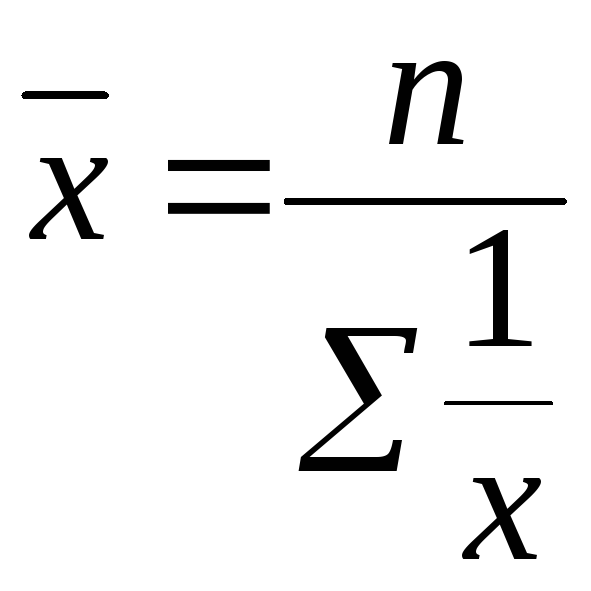

4.Средняя гармоническая взвешенная применяется, когда неизвестны веса, а имеется произведение варианты на частоту — .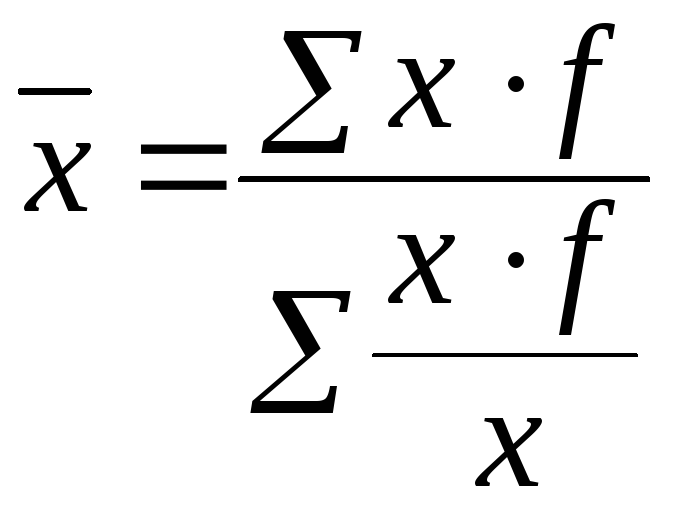

Задание решается с помощью выборочного метода. Выборочное наблюдение – это такое несплошное наблюдение, при котором отбор подлежащих обследованию единиц осуществляется в случайном порядке, отобранная часть изучается, а результаты распространяются на всю совокупность.

Для нахождения предельных ошибок выборки используются следующие формулы:

1. При повторном способе отбора:

— для средней количественного признака:

, где— выборочная дисперсия (дисперсия признака в выборочной совокупности);n- объём выборки (число обследованных единиц);

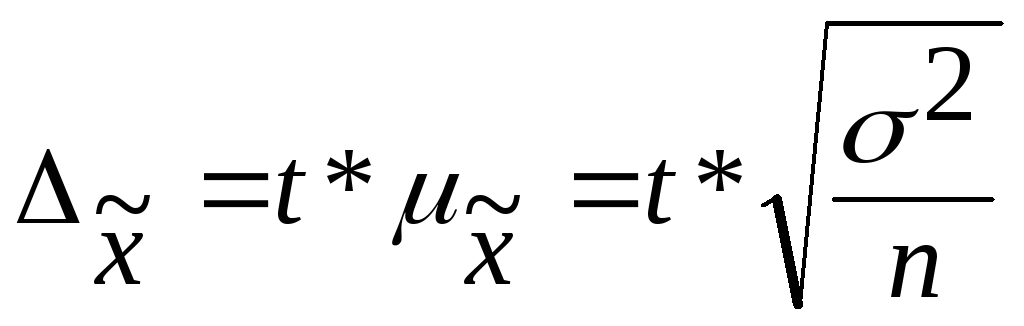
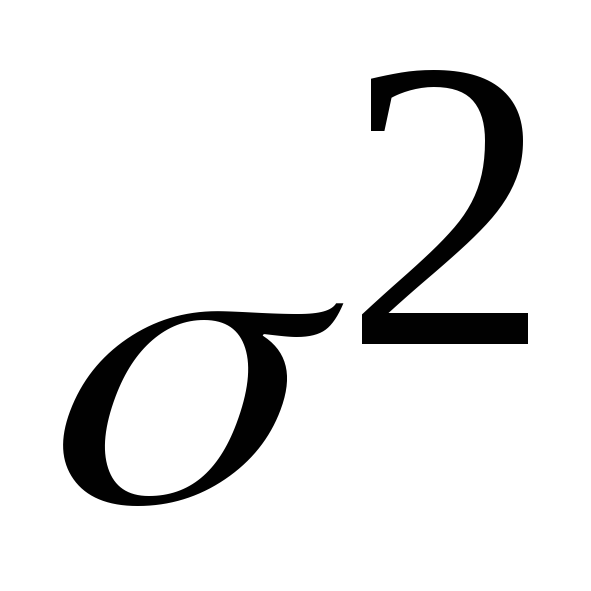
t— где нормированное отклонение – «коэффициент доверия», зависящий от вероятности, с которой гарантируется предельная ошибка выборки;— средняя ошибка выборки.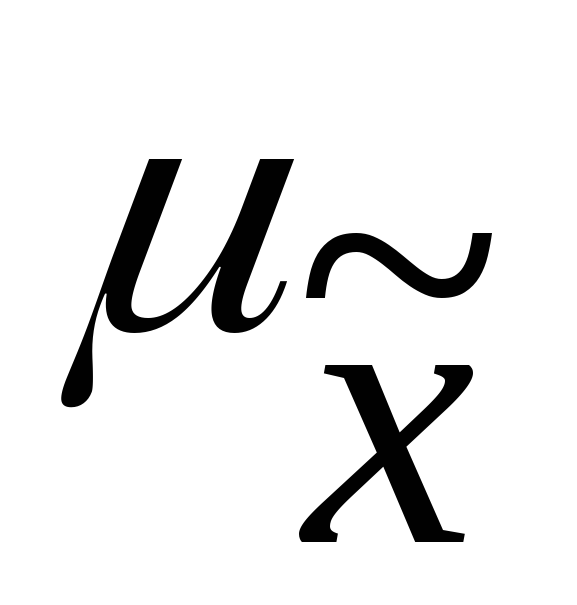

— для доли (альтернативного признака):

, где- выборочная доля (доля единиц, обладающих данным признаком в выборочной совокупности);

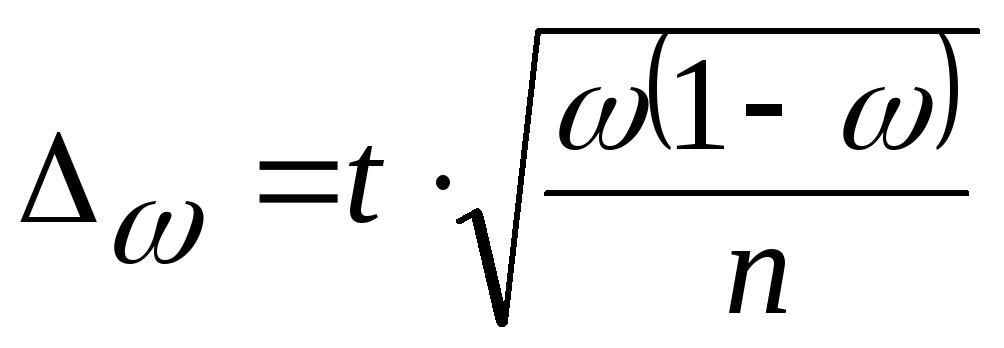
2. При бесповторном способе отбора

— для средней количественного признака

, гдеN —объем генеральной совокупности (число входящих в неё единиц);

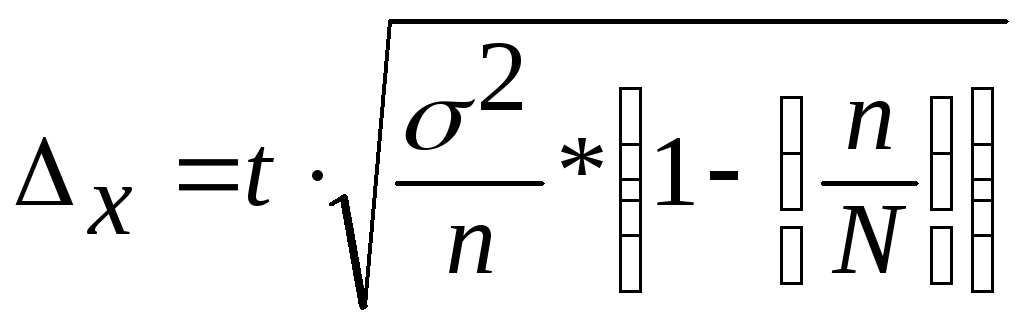
— для доли (альтернативного признака)

.

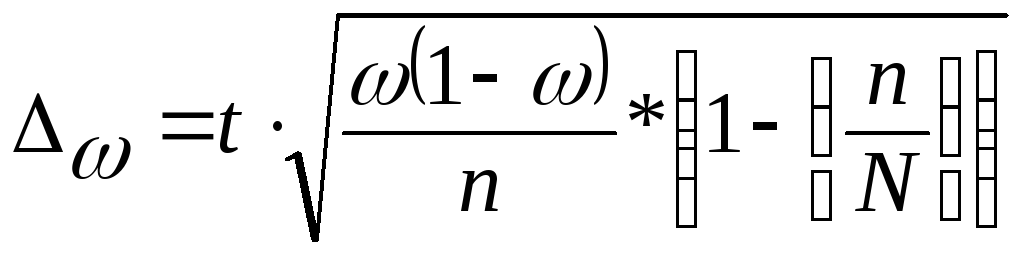
Необходимый объём выборки определяется по формулам.

При бесповторном способе отбора:

— для средней количественного признака ;

— для доли (альтернативного признака) .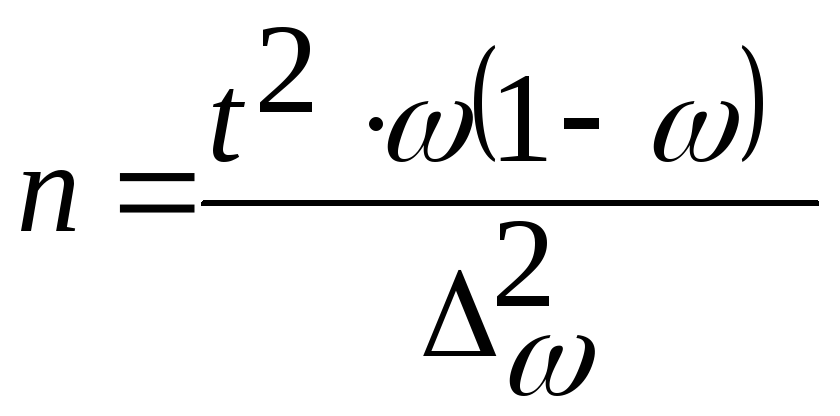

При повторном способе отбора:

— для средней количественного признака ;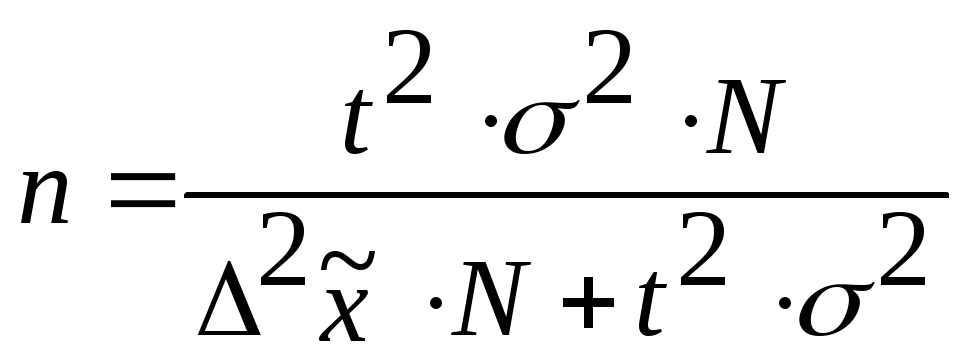

— для доли

Данная задача решается с помощь анализа рядов динамики. Формулы для расчета изменений от года к году следующие:

Источник

Статистические методы изучения инвестиций

Автор: Пользователь скрыл имя, 08 Февраля 2013 в 21:20, курсовая работа

Краткое описание

Цель данной курсовой работы — исследование статистических методов изучения инвестиций.

Оглавление

Введение
1. Теоретическая часть
1.1. Статистика инвестиций
1.2. Характеристика инвестиционного процесса
1.3. Статистические методы
2. Расчетная часть
2.1 Задание 1
2.2 Задание 2
2.3 Задание 3
2.4 Задание 4
3. Аналитическая часть
3.1 Постановка задачи
3.2 Методика решения задачи
3.3 Технология выполнения компьютерных расчетов
3.4 Анализ результатов статистических компьютерных расчетов
Заключение
Список использованной литературы

Файлы: 1 файл

Курсовая работа Статистика.doc

3.2. Находим долю ( ) предприятий с инвестициями в основной капитал 5,0 млн руб. и более:

Среднюю ошибку выборочной доли находим по формуле бесповторного отбора:

Для вероятности 0,954 находим t=2. Предельную ошибку доли находим по формуле:

Генеральная доля , а доверительные пределы генеральной доли исчисляем, исходя из двойного неравенства:

Таким образом, с вероятностью 0,954 можно утверждать, что ошибка выборки доли предприятий с инвестициями в основной капитал 5,0 млн. руб. и более составит 16,2%. Генеральная доля будет находиться в пределах [7,8; 40,2].

Динамика инвестиций в промышленность региона характеризуется следующими (неполными) данными:

Таблица 2.11. Исходные данные

Инвестиции, млн руб. (y_i)

По сравнению с предыдущим годом

Абсолютное значение 1% прироста,

1. Определите инвестиции за каждый год; недостающие показатели анализа ряда динамики, которые внесите в таблицу;
2. Определите средний темп роста и прироста.

3) Осуществите прогноз размера инвестиций на следующие два года на основе найденного среднегодового темпа роста.

4.1. Для расчёта недостающих показателей воспользуемся формулами:

а. Определим темп прироста за 2 год по формуле:

б. Найдём абсолютный прирост за 2 год:

в. Найдем инвестиции за 1, 2 и 3 года:

y₂ = ∆y₂ / ∆T₂ * T = 30 / 2 * 102 = 1530,00 млн руб.

y₁ = y₂ / T * 100 = 30 / 2 * 102 = 1530,00 / 102 * 100 = 1500,00 млн руб.

y₃ = y₂ + ∆y₃ = 1530,00 + 40,00 = 1570,00 млн руб.

г. Определим Т, ∆T и А за третий год:

Т₃ = y₃ / y₂ * 100 = 1570,00 / 1530,00 * 100 = 102,6 %

д. Найдём Т, y, ∆y, А за 4 год:

y₄ = y₃ / 100 * Т₄ = 1570,00 / 100 * 103 = 1617,10 млн руб.

∆y₄ = y₄ — y₃ = 1617,10 – 1570,00 = 47,10 млн руб.

е. Определим y, T, ∆T, А за 5 год:

y₅ = y₄ + ∆y₅ = 1617,10 + 56,9 = 1674,00 млн руб.

Т₅ = y₅ / y₄ * 100 = 1674,00 / 1617,10 * 100 = 103,5 %

4.2. а. Определим средний темп роста ( ):

где n – количество лет;

k_i – коэффициент динамики;

k₁ = Т₁ / 100 = 102,0 / 100 = 1,02, и т.д.

б. Найдём средний темп прироста (∆ ):

∆ = – 100% = 102,7 – 100 = 2,7 % (2.26)

4.3. Найдём размер инвестиций на следующие два года на основе найденного среднегодового темпа роста:

Размер инвестиций на шестой год (y₆) составят:

y₆ = y₅ / 100 * = 1674,00 / 100 * 102,7 = 1714,18 млн руб.

Размер инвестиций на седьмой год (y₇) составят:

y₇ = y₆ / 100 * = 1714,18 / 100 * 102,7 = 1760,46 млн руб.

3. Аналитическая часть

3.1 Постановка задачи

Одной из важнейших задач статистического изучения инвестиций является определение объемов инвестиций, их структуры и темпов изменения. Структура финансовых инвестиций изучается с помощью их группировки по видам активов и направлениям инвестирования. В финансовых инвестициях особо выделяются иностранные инвестиции.

Иностранные инвестиции в экономику России — вложения капитала иностранными инвесторами, а также зарубежными филиалами российских юридических лиц в объекты предпринимательской деятельности на территории России в целях получения дохода. Инвестиции делятся на прямые, портфельные и прочие. 2

Изучение изменений анализируемых показателей во времени, то есть их динамика, проводится при помощи анализа рядов динамики. Анализ интенсивности изменения во времени осуществляется с помощью показателей, получаемых в результате сравнения уровней, к таким показателям относятся: абсолютный прирост (показывает прирост (сокращение) объема инвестиций по годам и абсолютное изменение по сравнению с 2006г.), темп роста (показывает, какую часть уровня, с которым производится сравнение, составляет сравниваемый уровень), темп прироста (показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения), абсолютное значение одного процента прироста. Система средних показателей включает средний уровень ряда, средний темп роста, средний темп прироста.

По данным, представленным в таблице 3.1 необходимо:

• определить цепной и базисный абсолютный прирост к 2006 году;
• рассчитать цепные и базисные темпы роста и прироста, абсолютное значение 1% прироста;
• определить среднегодовой темп роста и прироста;
• осуществить прогноз базисных темпов роста иностранных инвестиций на 2011 и 2012 года, при условии сохранения среднего абсолютного прироста;

Таблица 3.1. Объем и структура инвестиций, поступивших от иностранных инвесторов 1

Источник