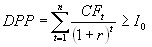Определить сроки окупаемости проектов с учетом дисконтирования

Дисконтированный период окупаемости

Дисконтированный срок окупаемости — характеризует изменение покупательной способности денег, то есть их стоимости, с течением времени. На его основе производят сопоставление текущих цен и цен будущих лет.

Дисконтированный срок окупаемости разумно понимать как тот срок, в расчете на который вложение средств в рассматриваемый проект даст ту же сумму денежных потоков, приведенных по фактору времени (дисконтированных) к настоящему моменту, которую за этот же срок можно было бы получить с альтернативного доступного для покупки инвестиционного актива.

Для инвестиционного планирования и выбора антикризисных инвестиционных проектов показатель дисконтированного срока окупаемости проекта практически важен в первую очередь тем, что он указывает на тот горизонт времени в бизнес-плане инвестиционного проекта, в пределах которого план-прогноз денежных потоков по проекту должен быть особенно надежным.

Калькулятор расчета дисконтированного срока окупаемости

Формула расчета дисконтированного срока окупаемости

• n – число периодов;
• CFt – приток денежных средств в период t;
• r – барьерная ставка (коэффициент дисконтирования);
• Io – величина исходных инвестиций в нулевой период.

Пример расчета дисконтированного срока окупаемости инвестиций

Показатель	Значение, у.е.
Размер инвестиции	49 450,0
Доходы от инвестиций:
в первом году	13 760,0
во втором году	17 630,0
в третьем году	18 812,5
в четвертом году	16 447,5
Размер барьерной ставки	9,2%

Определим дисконтированный срок окупаемости инвестиционного проекта.

Пересчитаем денежные потоки в вид текущих стоимостей:

1. PV1 = 13760 / (1 + 0,092) = 12693,73 у.е.
2. PV2 = 17630 / (1 + 0,092) 2 = 15003,54 у.е.
3. PV3 = 18812,5 / (1 + 0,092) 3 = 14769,26 у.е.
4. PV4 = 16447,5 / (1 + 0,092) 4 = 11911,95 у.е.

Определим период по истечении которого инвестиция окупается.

Сумма дисконтированных доходов за 1 и 2 года: 12693,73 + 15003,54 = 27 697,27 у.е., что меньше суммы вложений (инвестиций) – 49450 у.е..

Сумма дисконтированных доходов за 1, 2 и 3 года: 42 466,52 у.е., что также меньше суммы первоначальных инвестиций.

Сумма дисконтированных доходов за 4 года составила 54 378,47 у.е., что больше размера инвестиций и это значит, что возмещение первоначальных инвестиционных расходов произойдет раньше 4 лет.

Если предположить что приток денежных средств поступает равномерно в течении всего периода (по умолчанию предполагается что денежные средства поступают в конце периода), то можно вычислить остаток от четвертого года.

Остаток = (1 — (54378,47 — 49450,00)/11911,95) = 0,59 года

То есть дисконтированный срок окупаемости инвестиций равен 3,59 года

Источник

Задача — Срок окупаемости проекта простым способом и с учетом дисконтирования

Определить срок окупаемости проекта простым способом и с учетом дисконтирования по двум вариантам.

Данные для расчетов:

Капиталовложения, тыс. руб.	Ежегодный доход, тыс. руб.	Ставка дисконтирования, %
		Вариант А	Вариант Б
600	95	8	10

Решение

Формула расчета срока окупаемости простым способом выглядит следующим образом:

К – первоначальные инвестиции,

Дп – среднегодовая стоимость денежных поступлений от реализации инвестиционного проекта.

Окупаемость проекта с учетом дисконтирования рассчитывается на основе коэффициента дисконтирования.

Коэффициент дисконтирования (Кд) считается по сложным процентам (единицу делит на (1+ставка дисконта) в степени, соответствующей числу лет, за которые мы производим дисконтирование):

Д – норма дисконта,

Дисконтированное значение дохода можно получить, умножив ежегодный доход на коэффициент дисконтирования. Формула расчета срока окупаемости выглядит следующим образом:

Т = период до момента окупаемости + денежный поток на момент окупаемости/дисконтированный денежный поток в год окупаемости.

Произведем расчеты для двух вариантов проектов:

Коэффициент дисконтирования при ставке 8%:

1-й год Кд = 1 / (1 + 0,08)^ 1 ≈ 0,926

2-й год Кд = 1 / (1 + 0,08)^ 2 ≈ 0,857

3-й год Кд = 1 / (1 + 0,08)^ 3 ≈ 0,794

4-й год Кд = 1 / (1 + 0,08)^ 4 ≈ 0,735

5-й год Кд = 1 / (1 + 0,08)^ 5 ≈ 0,681

6-й год Кд = 1 / (1 + 0,08)^ 6 ≈ 0,630

7-й год Кд = 1 / (1 + 0,08)^ 7 ≈ 0,583

8-й год Кд = 1 / (1 + 0,08)^ 8 ≈ 0,540

9-й год Кд = 1 / (1 + 0,08)^ 9 ≈ 0,500

10-й год Кд = 1 / (1 + 0,08)^ 10 ≈ 0,463

Для нахождения дисконтированного дохода необходимо каждый годовой доход умножить на соответствующий коэффициент дисконтирования. Результаты расчетов приведены в таблице ниже:

Период времени	Стоимость проекта, тыс. руб.	Денежные поступления, тыс. руб.	Коэффициент дисконтирования	Дисконтированный доход, тыс. руб.	Кумулятивная стоимость, тыс. руб.
0	600	—	—	—	-600
1	—	95	0,926	88	-512
2	—	95	0,857	81	-431
3	—	95	0,794	75	-355
4	—	95	0,735	70	-285
5	—	95	0,681	65	-221
6	—	95	0,630	60	-161
7	—	95	0,583	55	-105
8	—	95	0,540	51	-54
9	—	95	0,500	48	-7
10	—	95	0,463	44	37
Итого	600	950	637

Срок окупаемости проекта простым способом составляет: 600 / 95 = 6,32 года или 6 лет и 4 месяца (6 + 0,32*12).

Срок окупаемости проекта с учетом дисконтирования составляет: 9 + (7/44) = 9,16 лет или 9 лет и 2 месяца (9 + 0,16*12).

Коэффициент дисконтирования при ставке 10%:

1-й год Кд = 1 / (1 + 0,1)^ 1 ≈ 0,909

2-й год Кд = 1 / (1 + 0,1)^ 2 ≈ 0,826

3-й год Кд = 1 / (1 + 0,1)^ 3 ≈ 0,751

4-й год Кд = 1 / (1 + 0,1)^ 4 ≈ 0,683

5-й год Кд = 1 / (1 + 0,1)^ 5 ≈ 0,621

6-й год Кд = 1 / (1 + 0,1)^ 6 ≈ 0,564

7-й год Кд = 1 / (1 + 0,1)^ 7 ≈ 0,513

8-й год Кд = 1 / (1 + 0,1)^ 8 ≈ 0,467

9-й год Кд = 1 / (1 + 0,1)^ 9 ≈ 0,424

10-й год Кд = 1 / (1 + 0,1)^ 10 ≈ 0,386

Для нахождения дисконтированного дохода необходимо каждый годовой доход умножить на соответствующий коэффициент дисконтирования. Результаты расчетов приведены в таблице ниже:

Период времени	Стоимость проекта, тыс. руб.	Денежные поступления, тыс. руб.	Коэффициент дисконтирования	Дисконтированный доход, тыс. руб.	Кумулятивная стоимость, тыс. руб.
0	600	—	—	—	-600
1	—	95	0,909	86	-514
2	—	95	0,826	79	-435
3	—	95	0,751	71	-364
4	—	95	0,683	65	-299
5	—	95	0,621	59	-240
6	—	95	0,564	54	-186
7	—	95	0,513	49	-138
8	—	95	0,467	44	-93
9	—	95	0,424	40	-53
10	—	95	0,386	37	-16
Итого	600	950	584

Срок окупаемости проекта простым способом составляет: 600 / 95 = 6,32 года или 6 лет и 4 месяца (6 + 0,32*12).

Как видно из таблицы, кумулятивный денежный поток отрицателен на конец 10 года, что говорит о том, что с учетом дисконтирования срок окупаемости превысит 10 лет. Срок окупаемости с учетом дисконтирования составит: 10 + (16/95*(1/(1 + 0,1)^ 11 )) = 10,48 лет или 10 лет и 6 месяцев (10 + 0,48*12).

Ответ: срок окупаемости проектов А и Б простым способом составит 6 лет и 4 месяца, а с учетом дисконтирования проект А окупится за 9 лет и 2 месяца, а проект Б – за 10 лет и 6 месяцев.

Источник

Discovered

О финансах и не только…

Дисконтированный срок окупаемости инвестиций

Что такое дисконтированный срок окупаемости?

Дисконтированный срок окупаемости (Discounted Pay-Back Period, DPP) — это срок, требуемый для возврата вложенных инвестиций в проект за счёт чистого денежного потока с учётом ставки дисконтирования.

Дисконтированный срок окупаемости является одним из ключевых показателей оценки эффективности инвестиционного проекта. Сущность метода дисконтированного срока окупаемости заключается в том, что из первоначальных затрат на реализацию инвестиционного проекта последовательно вычитают дисконтированные денежные доходы с тем, чтобы окупить (покрыть) инвестиционные расходы.

Дисконтирование денежных потоков позволяет учесть изменение стоимости денег во времени, т.е. осуществляется учёт изменения покупательной способности денег. Это особенно актуально в условиях нестабильности национальной денежной единицы.

Ставка дисконтирования, используемая в процессе расчёта срока окупаемости, позволяет учесть не только ожидаемый уровень инфляции, но и норму доходности, приемлемую для инвестора. Всё это, в конечном итоге, позволяет более точно определить срок окупаемости инвестиционного проекта.

В экономической литературе дисконтированный срок окупаемости инвестиций имеет ряд синонимов: дисконтированный период окупаемости капиталовложений, окупаемость в терминах текущих стоимостей, Discounted Payback Period, DPP, Present Value Payback, PVP.

Формула расчёта дисконтированного срока окупаемости инвестиций

Для расчёта дисконтированного срока окупаемости инвестиций применяется следующая формула:

где
DPP (Discounted Pay-Back Period) – дисконтированный срок окупаемости инвестиций;
IC (Invest Capital) – размер первоначальных инвестиций;
CF (Cash Flow) – денежный поток, генерируемый инвестиционным проектом;
r – ставка дисконтирования;
n – срок реализации проекта.

Ставка дисконтирования (или барьерная ставка) — это ставка при помощи которой осуществляется приведение величины денежного потока в n-ом периоде к единой величине текущей стоимости. При этом ставка дисконтирования может быть как единой (фиксированной) для всех периодов, так и переменной.

Инвестиционный проект считается эффективным, если сумма дисконтированных потоков от его реализации превышает сумму первоначальных инвестиций (т.е. наступает окупаемость проекта), а также если срок окупаемости не превышает некую пороговую величину (например, срок окупаемости альтернативного инвестиционного проекта).

Примеры расчёта дисконтированного срока окупаемости инвестиций

Предположим, что первоначальные инвестиции в проект составляют 500 тыс., а денежные потоки на протяжении 7 лет реализации проекта имеют значения, как приведено в таблице ниже. Дисконтирование будем осуществлять по ставке 10% годовых.

Приведённые данные свидетельствуют о том, что при первоначальных инвестициях в 500 тыс. за 7 лет суммарные денежные потоки по проекту составят 745 тыс., при этом за первые 5 лет денежные потоки, генерируемые проектом, составят 500 тыс., т.е. окупаемость проекта составляет ровно 5 лет. Но это простой расчёт, который не учитывает стоимость денег во времени.

Если же продисконтировать ожидаемые денежные потоки по ставке 10%, то окупаемость проекта составит практически 7 лет, т.к. накопительный дисконтированный денежный поток за 7 лет превысит первоначальную сумму инвестиций.

Как отмечалось выше, ставка дисконтирования может быть не только фиксированной, но и переменной величиной. На размер ставки дисконтирования могут оказывать влияние ряд факторов, в частности, инфляционные ожидания, стоимость привлечения ресурсов, изменение доходности альтернативных инвестиционных инструментов и т.п. Рассмотрим пример расчёта дисконтированного срока окупаемости с разными уровнями ставки дисконтирования.

Коэффициент дисконтирования определяем по стандартной формуле (1 + r) n . Например, в нашем случае для третьего года коэффициент дисконтирования составит:

То есть, при расчёте коэффициента дисконтирования для третьего года используются ставки дисконтирования соответственно за первый, второй и третий год.

Разделив денежный поток периода на соответствующий ему коэффициент дисконтирования, получим дисконтированный денежный поток. Как и в первом примере, дисконтированный срок окупаемости инвестиций составит 7 лет.

Преимущества и недостатки метода дисконтированного срока окупаемости

Дисконтированный срок окупаемости позволяет:

• учесть изменение стоимости денег во времени;
• применить разные ставки дисконтирования для отдельных периодов.

Недостатки метода дисконтированного срока окупаемости инвестиций:

• не учитывается размер денежных потоков после точки безубыточности;
• происходит искажение вычисляемых результатов при непостоянных денежных потоках с различным знаком.

Источник