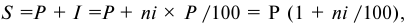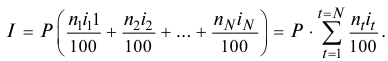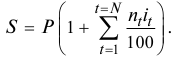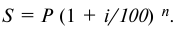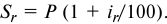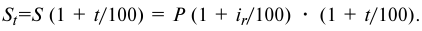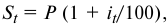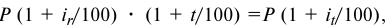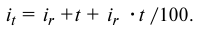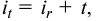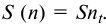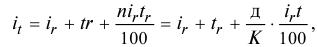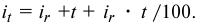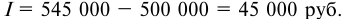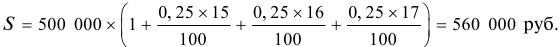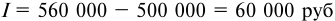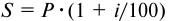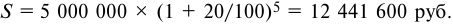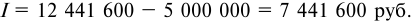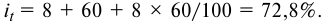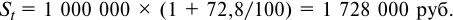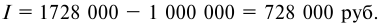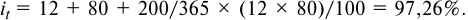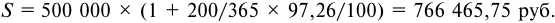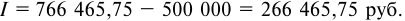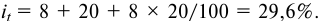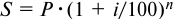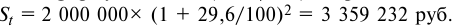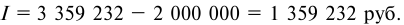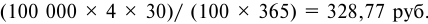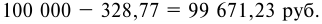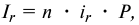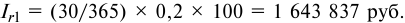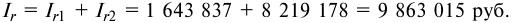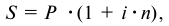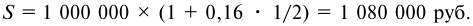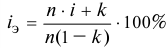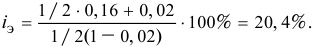Определить реальную доходность операции если кредит выдается
если = а (доходность вложений и уровень инфляции равны), то = О, т. е. весь доход поглощается инфляцией;
если а (доходность вложений вьпие уровня инфляции), то гс > О, т. е. происходит реальный прирост вложенного капитала.
Кредит в размере 50 ООО ООО руб. вьщан на два года. Реальная доходность операции должна составить 10% годовых по сложной ставке ссудного процента. Ожидаемый уровень инфляции составляет 15% в год. Определить множитель наращения, сложную ставку процентов, учитывающую инфляцию, и наращенную сумму.
По формуле (6.3) получаем
Множитель наращения и номинальная ставка доходности равны:
/: .с = (1 + 0,1)2. 1,3225 = 1,6; = (1 + 0,1) 21,3225 — 1 = 0,265 = 26,5%. Далее для наращенной суммы получаем
5= 50 000 000(1 + 0,265)2 = 80 011 250 (руб.). ,
Первоначальный капитал в размере 20 ООО ООО руб. вьщается на три года, проценты начисляются в конце каждого квартала по номинальной ставке 8% годовых. Определить номинальную ставку процентов и наращенную сумму с учетом инфляции, если ожидаемый годовой уровень инфляции составляет 12%.
Воспользуемся формулой (6.3): :8(>
4 = (1 + 0,12)3 = 1,4. )птХ.
По формуле (6.9) имеем
Ja = [(1 + 0,08/4) VM — 1] 4 = 0,107 = 10,7%. Отсюда
S=20 ООО ООО (1 + 0,107/4)2 = 27 454 048 (руб.). Пример 24
При вьщаче кредита должна быть обеспечена реальная доходность операции, определяемая учетной ставкой 5% годовых. Кре-
дит вьщается на полгода, за которые предполагаемый индекс инфляции составит 1,06. Рассчитать значение учетной ставки, компенсирующей потери от инфляции. Решение
Производим вычисления по формуле (6.7):
4, = (1,06-1 + 0,5 0,05)/(1,06 . 0,5) = 0,16 = 16%.
Определить реальную доходность финансовой операции, если при уровне инфляции 0,9% в месяц вьщается кредит на два года по номинальной ставке сложных процентов 15% годовых. Проценты начисляются ежеквартально.
Принимая заданную номинальную процентную ставку за ставку, учитывающую инфляцию, получим из формулы (6.9) соотно-щение для определения реальной номинальной ставки сложных процентов: —
= (1 + 0,009)2 = (1,009) = l,027
У= [0,15 + 4(1 — 1,027)]/1,027 = 0,038 = 3,8%. Пример 26
Определить, какой реальной убыгочностью обладает финансовая операция, если при уровне инфляции 14% в год капитал вкладывается на один год под номинальную ставку 8% при ежемесячном начислении.
Находим сначала индекс инфляции:
/и = 1 + 0,14 = 1,14. Далее используем формулу (6.15):
J= [0,08 + 12(1 — VU4 )]/ %fri4 = -0,051 = -5,1%. Таким образом, данная операция будет приносить 5,1%-ный убыток.
В большинстве современных коммерческих операций подразумеваются не разовые платежи, а последовательность денежных поступлений (или, наоборот, выплат) в течение определенного периода. Это может быть серия доходов и расходов некоторого предприятия, вьшлата задолженностей, регулярные или нерегулярные взносы для создания разного рода фондов и т. д. Такая последовательность называется потоком платежей.
Поток однонаправленных платежей с равными интервалами между последовательными платежами в течение определенного количества лет называется аннуитетом (финансовой рентой).
Теория аннуитетов является важнейшей частью финансовой математики. Она применяется при рассмотрении вопросов доходности ценных бумаг, в инвестиционном анализе и т. д. Наиболее распространенные примеры аннуитета: регулярные взносы в пенсионный фонд, погашение долгосрочного кредита, выплата процентов по ценным бумагам.
Аннуитеты различаются между собой следующими основными характеристиками:
величиной каждого отдельного платежа;
интервалом времени между двумя последовательными платежами (периодом аннуитета);
сроком от начала аннуитета до конца его последнего периода (бываюти неограниченные по времени — вечные аннуитеты);
процентной ставкой, применяемой при наращении или дисконтировании платежей.
Аннуитет, для которого платежи осуществляются в начале соответствующих интервалов, носит название аннуитета пренуме-рандо; если же платежи осуществляются в конце интервалов, мы получаем аннуитет постнумерандо (обыкновенный аннуитет) -пожалуй, самый распространенный случай.
Наибольший интерес с практической точки зрения представляют аннуитеты, в которых все платежи равны между собой (постоянные аннуитеты), либо изменяются в соответствии с некоторой закономерностью. Именно такие аннуитеты мы и изучим в дальнейшем.
Введем следующие обозначения; Р — величина каждого отдельного платежа; ic — сложная процентная ставка, по которой начисляются проценты;
Sk — наращенная сумма для -го платежа аннуитета постнумерандо;
S — наращенная (будущая) сумма всего аннуитета постнумерандо (т. е. сумма всех платежей с процентами);
Ак — современная величина -го платежа аннуитета постнумерандо;
А — современная величина всего аннуитета постнумерандо
(т. е. сумма современных величин всех платежей); Sn — наращенная сумма аннуитета пренумерандо; An — современная величина аннуитета пренумерандо; п — число платежей.
Рассмотрим аннуитет постнумерандо с ежегодными платежами Ръ течение п лет, на которые начисляются проценты по сложной годовой ставке (рис. 5).
Рис. 5. Будущая стоимость аннуитета постнумерандо
Сумма S для первого платежа, проценты на который будут начисляться, очевидно, (п — I) раз, составит по формуле (3.1):
Для второго платежа (проценты на него будут начисляться на Один год меньше) имеем
и так далее. На последний платеж, произведенный в конце л-го года, проценты уже не начисляются, т. е.
Тогда для общей наращенной суммы имеем
Д /,й — коэффициент наращения аннуитета с параметрами /, п — представляет собой, как можно заметить, сумму членов геометрической прогрессии, для которой первый член а, равен 1, а знаменатель (назовем его q) составляет (1 -I- /).
Используя математическую формулу для суммы членов геометрической прогрессии:
запищем выражение (7.1) в более удобном для вычислений виде:
Для коэффициента наращения, соответственно, имеем
, (1 + — 1 . . Кп =-J- : (7.3)
Найдем теперь современную величину А данного аннуитета (рис. 6).
Рис. 6. Современная величин аннуитета постнумерандо
При заданной процентной ставке современное значение каждого платежа будет определяться по формуле:
Современная величина всего аннуитета, следавательно, соста-
J.дe д. — коэффициент приведения аннуитета, опять является сулшбй геометрической прогрессии, теперь уже с параметрами а = д= 1/(1 + д. Тогда для а,- получаем выражение:
для современной величины А соответственно
Как видим, современная величина и наращенная сумма аннуитета связаны между собой соотнощением:
Из полученных формул путем преобразований легко получить еще несколько формул. Так, для определения размера очередного платежа (Р) имеем
с;, 1 — (1 + g Для определения срока аннуитета (и), при прочих заданных ус-
Для конкретных вычислений выбирается одна из двух формул каждой пары в зависимости от заданных известных величин.
Рассмотрим далее аннуитет пренумерандо с теми же начальными условиями (рис. 7).
Очевидно, отличие от предьщущего случая состоит здесь в том, что период начисления процентов на каждый платеж увеличива-
Источник
Кредитные операции с примерами решения задач
Кредитные операции
Кредитные операции играют основную роль в деятельности банков. Ставка, по которой выдаются кредиты, превышает ставку, по которой принимаются депозиты, на величину процентной маржи, которая и является источником прибыли банка от кредитных операций. При погашении кредита удобно сразу определять размер возвращаемой (погашаемой) суммы, равной сумме кредита 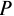
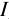
где 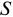
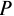
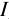
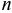
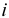
Если ставка процентов в течение срока кредита по условиям кредитного договора будет изменяться, размер погашаемой суммы можно определить, применяя формулу 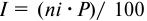
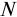
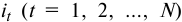
Сумма кредита с процентами определяется по формуле
При выдаче кредитов на срок больше года проценты могут начисляться по сложной годовой ставке. Погашаемая сумма кредита может быть при этом определена с использованием формулы
При начислении процентов за кредит следует учитывать инфляцию. Ставку процентов при выдаче кредитов в условиях инфляции можно определить следующим образом. Если задана реальная доходность кредитной операции, определяемая простой ставкой процентов 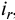
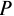
Эквивалент такой суммы в условиях инфляции составит:
С другой стороны, величину 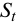
где 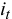
Приравняв два последних выражения, получаем
откуда простая ставка процентов, обеспечивающая реальную эффективность кредитной операции 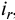
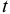
При проведении подобных расчетов часто пользуются приближенным выражением
из которого следует, что
Следовательно, если кредит был выдан по ставке 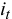
Если срок, на который выдается кредит, меньше срока, за который определяется расчетный уровень инфляции, необходимо задать зависимость значения 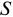
При заданном годовом уровне инфляции 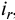
где 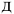
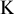
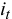
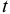
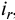
Задача 71.
Банк выдал кредит в размере 500 тыс. руб. на шесть месяцев по простой ставке процентов 18% годовых. Требуется определить:
1) погашаемую сумму.
2) сумму процентов за кредит.
Решение:
- Погашаемую сумму определим по формуле (5.1):
- Сумма процентов, полученная банком за кредит, будет равна:
Задача 72.
Банк выдал кредит в сумме 500 тыс. руб. на три квартала по простой ставке процентов, которая в первом квартале составила 15% годовых, а в каждом последующем увеличивалась на 1 процентный пункт. Требуется определить:
1) погашаемую сумму;
2) сумму процентов за пользование кредитом.
Решение:
1. По формуле (5.2) определяем погашаемую сумму:
- Сумму полученных процентов вычисляем так:
Задача 73.
Банк выдал долгосрочный кредит в размере 5 млн. руб. на пять лет по годовой ставке сложных процентов 20% годовых. Кредит должен быть погашен единовременным платежом с процентами в конце срока. Требуется определить:
1) погашаемую сумму
2) сумму полученных процентов.
Решение:
определяем погашаемую сумму:
- Сумму полученных процентов вычисляем так:
Задача 74.
Банк выдал кредит в 1 млн руб. на год. Требуемая реальная доходность операции равна 8% годовых, ожидаемый годовой уровень инфляции принят равным 60%. Требуется определить:
1) ставку процентов по кредиту.
2) погашаемую сумму и сумму полученных процентов.
Решение:
- По формуле (5.4) вычислим ставку процентов по кредиту:
- По формуле (5.3) определим погашаемую сумму:
Сумму полученных процентов определяем так:
Задача 75.
Кредит в 500 тыс. руб. выдан на 200 дней. Расчетный уровень инфляции за год принят равным 80%, реальная доходность операции должна составить 12% годовых, количество дней в году равно 365. Требуется определить:
1) ставку процентов при выдаче кредита
2) погашаемую сумму и сумму полученных процентов.
Решение:
- По формуле (5.5) определим ставку процентов:
- По формуле (5.1) определим погашаемую сумму:
Сумма полученных процентов составит:
Задача 76.
Кредит в 2 млн руб. выдан на два года. Реальная эффективность операции должна составить 8% годовых по сложной ставке процентов. Расчетный уровень инфляции 20% в год. Требуется определить:
1) ставку процентов при выдаче кредита;
2) погашаемую сумму и сумму полученных процентов. Решение
- По формуле (5.6) определяем ставку сложных процентов:
определим погашаемую сумму:
Сумма полученных процентов будет равна:
Задача 77.
Базовая годовая сумма оплаты обучения в вузе равна 2000 руб. и повышается с учетом инфляции (10%). Срок обучения пять лет. Вуз предлагает выплатить сразу 10 тыс. руб., оплатив весь срок обучения. Банковский процент на вклад составляет 12%, сумма вклада равна 12 тыс. руб. Требуется определить, выгодно ли это предложение для студента.
Решение:
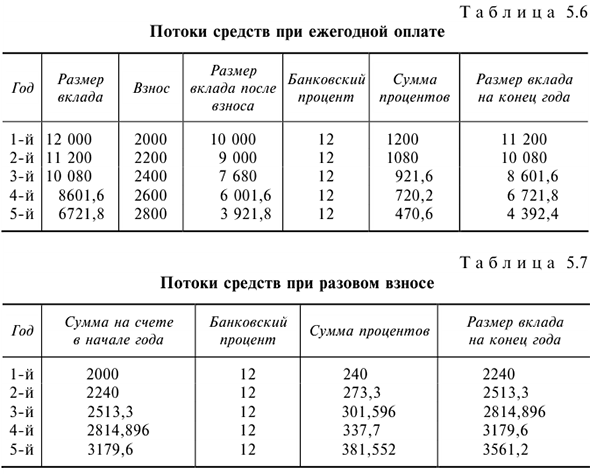
Проведем расчеты в табл. 5.6 и 5.7.
- Определим потоки средств при ежегодной оплате.
- Определим потоки средств при разовом взносе.
По результатам расчетов видно, что первый вариант выгоднее.
Задача 78.
В расчет за поставку фирма 
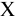
1) сумму дисконта;
2) сумму, которую банк выплачивает фирме 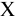
Решение:
Используем формулу расчета дисконта:
- Определяем выплачиваемую сумму:
Задача 79.
Заемщик берет ссуду на сумму 100 тыс. руб. сроком на шесть месяцев. Через шесть месяцев заемщик возмещает 102 тыс. руб., т.е. ссуду — 100 тыс. руб. и проценты — 2 тыс. руб. Требуется определить годовую ставку по ссуде.
Решение:
Задача 80.
Банк выдал в начале квартала кредит на сумму 100 млн руб. сроком на один месяц по ставке 20% годовых и через месяц кредит на сумму 200 млн руб. сроком на два месяца по ставке 25% годовых. Требуется определить сумму процентов за кредиты (полученный доход).
Решение:
где 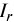
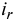
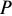
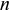
- Сумма процентов за первый кредит:
- Сумма процентов за второй кредит:
Задача 81.
Банк выдал ссуду в размере 1 млн руб. на шесть месяцев по простой ставке процентов 16% годовых. Требуется определить: сумму погашения.
Решение:
где 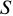
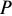
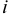
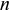
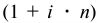
Задача 82.
При выдаче кредита на шесть месяцев по ставке 16% годовых удержаны комиссионные в размере 2% суммы кредита. Требуется определить доход банка с учетом удержания комиссионных.
Решение:
Используем следующую формулу:
где 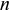
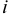
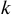
Доход банка составит в данном случае:
Эта лекция с примерами решения взята со страницы решение задач по предмету «деньги кредит банки»:
Возможно эти страницы вам будут полезны:
Изучу , оценю , оплатите , через 2-3 дня всё будет на «4» или «5» !
Откройте сайт на смартфоне, нажмите на кнопку «написать в чат» и чат в whatsapp запустится автоматически.
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Источник