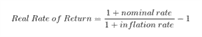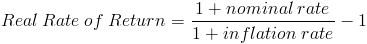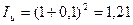Определить реальную доходность финансовой операции уровень инфляции

Реальная доходность с учетом инфляции

Целью любого инвестирования является не только сохранение, но и приумножение денежных средств. Доходность – основной показатель эффективности инвестиционных вложений. Но в мире есть такое явление, как инфляция. И мы все знаем, что несколько лет назад на 100 тысяч рублей можно было купить больше товаров, чем сейчас. Инфляция может скорректировать доход инвестора и не в лучшую сторону. Поэтому для того, чтобы грамотно оценить свои инвестиции, надо обязательно учитывать влияние инфляции. Некоторые инвесторы делают это с помощью простого вычитания процента инфляции из номинальной доходности. Но этот метод не является точным. Для того, чтобы рассчитать реальную доходность с учетом инфляции надо воспользоваться соответствующей формулой.

Формула расчета доходности

Предположим, вы положили на депозит 1000 рублей при ставке 8% годовых. Инфляция – 5 процентов.

Через 10 лет эта тысяча превратится в 2159 рублей.

Рассчитана эта сумма так:

А теперь посмотрим, как за этот период вырастут потребительские цены:

Исходя из полученных значений, посчитаем реальную доходность. Для этого нужно разделить сумму депозита через 10 лет на значение инфляции:

Но для анализа удобней оперировать значениями в процентах.

Переводим полученную сумму в %:

(1324/1000)^1/10 -1 *100 = 2,8%.

Итак, мы выяснили, что реальная доходность с учетом инфляции при начальном депозите 1000 рублей составит 2,8%. А если бы мы посчитали ее по упрощенной формуле, то она бы составила 3% (8-5). Как видите, разница в размере дохода, рассчитанного двумя способам, есть.

Формулу расчета можно представить в таком виде:

Реальная доходность = (номинальная ставка доходности – уровень инфляции) / (1 + уровень инфляции)

Проверим на нашем примере насколько она верна:

(0,08 – 0,05) / (1 + 0,05) = 0,028

Умножаем на 100 и получаем реальную доходность 2,8%. Значение соответствует ранее произведенному расчету.

Могу предложить еще одну формулу для определения доходности, скорректированной на рост цен:

Real Rate of Return – это то, что нас интересует, то есть реальная доходность.

Nominal rate – это ставка доходности.

Inflation rate – уровень инфляции.

Проверяем эту формулу:

(1 + 0,08) / (1 + 0,05) -1 = 0,028 или 2,8%.

Какой из этих формул воспользоваться – решать вам. В любом случае реальная доходность с учетом инфляции, рассчитанная по каждой из них, будет правильной.

Источник

Определить реальную доходность финансовой операции уровень инфляции

если = а (доходность вложений и уровень инфляции равны), то = О, т. е. весь доход поглощается инфляцией;

если а (доходность вложений вьпие уровня инфляции), то гс > О, т. е. происходит реальный прирост вложенного капитала.

Кредит в размере 50 ООО ООО руб. вьщан на два года. Реальная доходность операции должна составить 10% годовых по сложной ставке ссудного процента. Ожидаемый уровень инфляции составляет 15% в год. Определить множитель наращения, сложную ставку процентов, учитывающую инфляцию, и наращенную сумму.

По формуле (6.3) получаем

Множитель наращения и номинальная ставка доходности равны:

/: .с = (1 + 0,1)2. 1,3225 = 1,6; = (1 + 0,1) 21,3225 — 1 = 0,265 = 26,5%. Далее для наращенной суммы получаем

5= 50 000 000(1 + 0,265)2 = 80 011 250 (руб.). ,

Первоначальный капитал в размере 20 ООО ООО руб. вьщается на три года, проценты начисляются в конце каждого квартала по номинальной ставке 8% годовых. Определить номинальную ставку процентов и наращенную сумму с учетом инфляции, если ожидаемый годовой уровень инфляции составляет 12%.

Воспользуемся формулой (6.3): :8(>

4 = (1 + 0,12)3 = 1,4. )птХ.

По формуле (6.9) имеем

Ja = [(1 + 0,08/4) VM — 1] 4 = 0,107 = 10,7%. Отсюда

S=20 ООО ООО (1 + 0,107/4)2 = 27 454 048 (руб.). Пример 24

При вьщаче кредита должна быть обеспечена реальная доходность операции, определяемая учетной ставкой 5% годовых. Кре-

дит вьщается на полгода, за которые предполагаемый индекс инфляции составит 1,06. Рассчитать значение учетной ставки, компенсирующей потери от инфляции. Решение

Производим вычисления по формуле (6.7):

4, = (1,06-1 + 0,5 0,05)/(1,06 . 0,5) = 0,16 = 16%.

Определить реальную доходность финансовой операции, если при уровне инфляции 0,9% в месяц вьщается кредит на два года по номинальной ставке сложных процентов 15% годовых. Проценты начисляются ежеквартально.

Принимая заданную номинальную процентную ставку за ставку, учитывающую инфляцию, получим из формулы (6.9) соотно-щение для определения реальной номинальной ставки сложных процентов: —

= (1 + 0,009)2 = (1,009) = l,027

У= [0,15 + 4(1 — 1,027)]/1,027 = 0,038 = 3,8%. Пример 26

Определить, какой реальной убыгочностью обладает финансовая операция, если при уровне инфляции 14% в год капитал вкладывается на один год под номинальную ставку 8% при ежемесячном начислении.

Находим сначала индекс инфляции:

/и = 1 + 0,14 = 1,14. Далее используем формулу (6.15):

J= [0,08 + 12(1 — VU4 )]/ %fri4 = -0,051 = -5,1%. Таким образом, данная операция будет приносить 5,1%-ный убыток.

В большинстве современных коммерческих операций подразумеваются не разовые платежи, а последовательность денежных поступлений (или, наоборот, выплат) в течение определенного периода. Это может быть серия доходов и расходов некоторого предприятия, вьшлата задолженностей, регулярные или нерегулярные взносы для создания разного рода фондов и т. д. Такая последовательность называется потоком платежей.

Поток однонаправленных платежей с равными интервалами между последовательными платежами в течение определенного количества лет называется аннуитетом (финансовой рентой).

Теория аннуитетов является важнейшей частью финансовой математики. Она применяется при рассмотрении вопросов доходности ценных бумаг, в инвестиционном анализе и т. д. Наиболее распространенные примеры аннуитета: регулярные взносы в пенсионный фонд, погашение долгосрочного кредита, выплата процентов по ценным бумагам.

Аннуитеты различаются между собой следующими основными характеристиками:

величиной каждого отдельного платежа;

интервалом времени между двумя последовательными платежами (периодом аннуитета);

сроком от начала аннуитета до конца его последнего периода (бываюти неограниченные по времени — вечные аннуитеты);

процентной ставкой, применяемой при наращении или дисконтировании платежей.

Аннуитет, для которого платежи осуществляются в начале соответствующих интервалов, носит название аннуитета пренуме-рандо; если же платежи осуществляются в конце интервалов, мы получаем аннуитет постнумерандо (обыкновенный аннуитет) -пожалуй, самый распространенный случай.

Наибольший интерес с практической точки зрения представляют аннуитеты, в которых все платежи равны между собой (постоянные аннуитеты), либо изменяются в соответствии с некоторой закономерностью. Именно такие аннуитеты мы и изучим в дальнейшем.

Введем следующие обозначения; Р — величина каждого отдельного платежа; ic — сложная процентная ставка, по которой начисляются проценты;

Sk — наращенная сумма для -го платежа аннуитета постнумерандо;

S — наращенная (будущая) сумма всего аннуитета постнумерандо (т. е. сумма всех платежей с процентами);

Ак — современная величина -го платежа аннуитета постнумерандо;

А — современная величина всего аннуитета постнумерандо

(т. е. сумма современных величин всех платежей); Sn — наращенная сумма аннуитета пренумерандо; An — современная величина аннуитета пренумерандо; п — число платежей.

Рассмотрим аннуитет постнумерандо с ежегодными платежами Ръ течение п лет, на которые начисляются проценты по сложной годовой ставке (рис. 5).

Рис. 5. Будущая стоимость аннуитета постнумерандо

Сумма S для первого платежа, проценты на который будут начисляться, очевидно, (п — I) раз, составит по формуле (3.1):

Для второго платежа (проценты на него будут начисляться на Один год меньше) имеем

и так далее. На последний платеж, произведенный в конце л-го года, проценты уже не начисляются, т. е.

Тогда для общей наращенной суммы имеем

Д /,й — коэффициент наращения аннуитета с параметрами /, п — представляет собой, как можно заметить, сумму членов геометрической прогрессии, для которой первый член а, равен 1, а знаменатель (назовем его q) составляет (1 -I- /).

Используя математическую формулу для суммы членов геометрической прогрессии:

запищем выражение (7.1) в более удобном для вычислений виде:

Для коэффициента наращения, соответственно, имеем

, (1 + — 1 . . Кп =-J- : (7.3)

Найдем теперь современную величину А данного аннуитета (рис. 6).

Рис. 6. Современная величин аннуитета постнумерандо

При заданной процентной ставке современное значение каждого платежа будет определяться по формуле:

Современная величина всего аннуитета, следавательно, соста-

J.дe д. — коэффициент приведения аннуитета, опять является сулшбй геометрической прогрессии, теперь уже с параметрами а = д= 1/(1 + д. Тогда для а,- получаем выражение:

для современной величины А соответственно

Как видим, современная величина и наращенная сумма аннуитета связаны между собой соотнощением:

Из полученных формул путем преобразований легко получить еще несколько формул. Так, для определения размера очередного платежа (Р) имеем

с;, 1 — (1 + g Для определения срока аннуитета (и), при прочих заданных ус-

Для конкретных вычислений выбирается одна из двух формул каждой пары в зависимости от заданных известных величин.

Рассмотрим далее аннуитет пренумерандо с теми же начальными условиями (рис. 7).

Очевидно, отличие от предьщущего случая состоит здесь в том, что период начисления процентов на каждый платеж увеличива-

Источник

Как правильно считать реальную доходность с учетом инфляции?

Автор: Алексей Мартынов · Опубликовано 03.07.2015 · Обновлено 02.12.2018

Наверно все знают, что реальная доходность — это доходность за вычетом инфляции. Все дорожает — продукты, товары, услуги. По данным Росстата за последние 15 лет цены выросли в 5 раз. Это означает, что покупательная способность денег, просто лежавших все это время в тумбочке уменьшилась в 5 раз, раньше могли купить 5 яблок, теперь 1.

Чтобы хоть как-то сохранить покупательную способность своих денег, люди их вкладывают в различные финансовые инструменты: чаще всего это депозиты, валюта, недвижимость. Более продвинутые используют, акции, ПИФы, облигации, драгметаллы. С одной стороны сумма вложений растет, с другой происходит их обесценивание из-за инфляции. Если из номинальной ставки доходности вычесть ставку инфляции, получится реальная доходность. Она может быть положительной или отрицательной. Если доходность положительная, ваши вложения приумножились в реальном выражении, то есть вы можете купить больше яблок, если отрицательная — обесценились.

Большинство инвесторов считают реальную доходность по простой формуле:

Но данный способ неточен. Приведу пример: возьмем 200 рублей и положим их на депозит на 15 лет со ставкой 12% годовых. Инфляция за этот период 7% в год. Если считать реальную доходность по простой формуле, то получится 12-7=5%. Проверим этот результат, посчитав на пальцах.

За 15 лет при ставке 12% годовых 200 рублей превратятся в 200*(1+0,12)^15=1094,71. Цены за это время вырастут в (1+0,07)^15=2,76 раз. Чтобы посчитать реальную доходность в рублях делим сумму на депозите на коэффициент инфляции 1094,71/2,76=396,63. Теперь, чтобы перевести реальную доходность в проценты считаем (396,63/200)^1/15 -1 *100% = 4,67%. Это отличается от 5%, то есть проверка показывает, что расчет реальной доходности «простым» способом не точен.
Чтобы правильно рассчитать реальную доходность, нужно применять формулу:

Real Rate of Return — реальная доходность
nominal rate — номинальная ставка доходности
inflation rate — инфляция

Проверяем:
(1+0,12)/(1+0,07)-1 * 100%=4,67% Сходится, значит формула верная.

Еще одна формула, которая дает тот же результат, выглядит так:

Источник

Определение реальной доходности операции в условиях инфляции

Дата добавления: 2015-01-16 ; просмотров: 3948 ; Нарушение авторских прав

В условиях инфляции важно также уметь определять реальную доходность операции, полученную при сложившемся уровне инфляции.

Из формулы (2.6) можно получить формулу, позволяющую определить реальную доходность финансовой операции, когда задан уровень инфляции и простая ставка процентов, учитывающая инфляцию.

. (2.12)

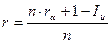
Пример 2.3.Срок операции составил полгода. При этом уровень инфляции в этот период был 2% в месяц. Определить реальную доходность такой операции, если простая ссудная ставка была 20% годовых.

За полгода индекс инфляции составил:

.

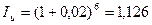
Тогда по формуле (2.12)

( –5,2%).

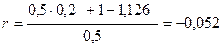
Проведенные расчеты показывают, что реально такая операция принесет убыток 5,2%.

Из формулы (2.8) получаем аналогичную формулу для случая сложных процентов:

. (2.13)

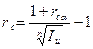
Пример 2.4.Клиент банка внес деньги на депозит сроком 2 года. Какова реальная доходность такого вложения под сложную ссудную ставку 15%, если уровень инфляции составит 10% в год.

Индекс инфляции составит за два года:

Тогда для определения реальной доходности используем формулу (2.13)

(4,5%).

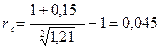
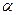
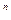
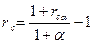
Подставив в формулу (2.13) вместо индекса инфляции выражение (1+ ) ,получим простую формулу

, (2.14)

отражающую несколько очевидных соображений:

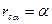
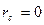
-если (доходность вложений и уровень инфляции равны), то , т. е. весь доход поглощается инфляцией;

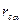
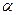
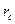
-если (доходность вложений выше уровня инфляции), то >0, т.е. происходит реальный прирост вложенного капитала.

Аналогично определяют формулы для учетных ставок.

Источник