- Формулы доходности финансовых операций
- Простая процентная ставка с учетом инфляции.
- Начисление процентов по кредитам и депозитам
- Начисление простой и сложной процентной ставки. Учет векселей с дисконтом. Долговые обязательства по учетной ставке. Реальная доходность финансовой операции банка. Составление плана погашения кредита. Погрешность при вычислении погасительного платежа.
- Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
- Подобные документы
Формулы доходности финансовых операций



Если в формулах наращения по процентной и учетной ставке принять срок n = 1 году, то получим, что
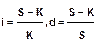
Если n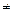
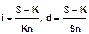
Эти формулы принято называть формулами доходности или эффективности по простой ставке процентов и учетной ставке соответственно.
Предприятие получило кредит на 1 год в размере 100 млн. с условием возврата 150 млн.
Найти доходность операции для кредитора в виде процентной и дисконтной (учетной) ставок.
К = 100 млн., S = 150 млн., n = 1 год. I = ?, d = ?
Решение:
Дисконтная ставка всегда меньше процентной, ибо она учитывает время более жестко.
Иногда размер дисконта в контрактах фиксируется за весь срок ссуды в виде доли (или процента) от суммы погасительного платежа. Таким образом, уровень процентной ставки задается в неявном виде. Выведем формулы, с помощью которых можно вычислить значения этих ставок.
Пусть S- размер погасительного платежа (сумма ссуды к концу срока),
dn – доля этого платежа, определяющая величину дисконта за весь срок ссуды.
К = S(1 – dn) – реально выдаваемая ссуда в момент заключения договора.
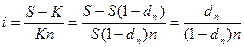 |
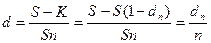 |
Задача 7.
Кредитор и заемщик договорились, что из суммы кредита, выданного на 200 дней, сразу удерживается дисконт в размере 25% указанной суммы. Требуется определить цену кредита в виде простой годовой учетной ставки d и годовой простой ставки i. Год полагать равным 365 дней.
Простые переменные ставки
В кредитных соглашениях иногда предусматриваются изменяющиеся во времени процентные ставки.
Если i1, i2,… ik – последовательные во времени простые ставки,
а n1, n2,… nk – периоды, в течение которых применяются соответствующие ставки, тогда наращенная сумма определяется следующим образом:
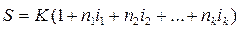 |
Контракт предусматривает следующий порядок начисления процентов: первый год – ставка 16%, в каждый последующем полугодии ставка повышается на 1%. Определить множитель наращения за 2,5 года.
Общий срок начисления процентов 1+1/2+1/2+1/2=2,5 года.
Множитель наращения =
Иначе, за 2,5 года начальный капитал увеличился в 1,43 раза.
Реинвестирование
В практике при реинвестировании средств в краткосрочные депозиты иногда прибегают к неоднократному последовательному повторению наращения по простым процентам в пределах заданного общего срока, т.е. к реинвестированию средств, полученных на каждом этапе наращения. (Напоминает наращение по сложным процентам, но только напоминает!)
В этом случае наращенная сумма для всего срока составит:
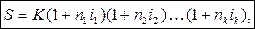
Если периоды начисления и ставки не изменяются во времени, то формула реинвестирования примет вид:
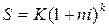
Задача 9.
Сумму в 100 тысяч рублей положили 1 января на месячный депозит под 20% годовых. Каковой будет наращенная сумма, если операция повторяется 3 раза? Расчет сделать по точным и банковским процентам.
По условию задачи депозит в 100 тысяч рублей реинвестируется трижды по простым процентам.
По точным процентам:
(Помните, что в январе 31 день, в феврале – 28 дней, в марте – 31 день!)
По банковским процентам при условии, что в каждом месяце по 30 дней:
Модуль 2. Сложные проценты
Наращение по сложным процентам
В среднесрочных и долгосрочных операциях, если проценты не выплачиваются сразу после их начисления, а присоединяются к сумме долга, то для наращения используются сложные проценты.
Сложные проценты отличаются от простых процентов базой начисления. Если в простых процентах она остается постоянной на весь срок начисления, то в сложных при каждом начислении процентные деньги присоединяются к первоначальной базе. Говорят, идет капитализация процентов.
Формула наращения по сложным процентам, если проценты начисляются один раз в году, имеет вид

(1) 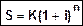
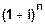
Задача 1.
Сумма, равная 800 тыс. руб., инвестируется на 3 года под 80% годовых. Найти наращенную сумму и сумму процентов за этот срок, используя простые и сложные проценты.
2. Простые проценты:
За 3 года 800 тыс. руб. увеличились в 5,832 раза по сложным процентам и только в 3,4 раза по простым процентам.
Задача 2.
Сумма, равная 800 тыс. руб., инвестируется на 3 месяца под 80% годовых. Найти наращенную сумму и сумму процентов за этот срок, используя простые и сложные проценты.
Источник
Простая процентная ставка с учетом инфляции.
При использовании простых процентов применяется формула:
 |
S — наращенная сумма без учета инфляции;
Sa — наращенная сумма с учетом инфляции (уровень a);
P — первоначальная сумма;
n — срок кредита в годах;
i — простая процентная ставка без учета инфляции (реальная доходность);
ia — простая процентная ставка с учетом инфляции.

|
 | (4.1) |
Пример 4.2. Кредит 50000 рублей выдан на 6 месяцев. Какова должна быть простая процентная ставка, если кредитор желает получить 10% реальной доходности, начисляемых по простой процентной ставке при уровне инфляции 20% в год? Вычислить наращенную сумму.
| Дано: | Решение: |
 n = 0,5 лет P = 50000 руб. α = 20% = 0,20 i = 10% = 0,10 n = 0,5 лет P = 50000 руб. α = 20% = 0,20 i = 10% = 0,10 | |
| ia = ? Sa = ? | Ответ: 57750 рублей. |
Существуют задачи и другого типа, связанные с инфляцией.
Пример 4.3. Кредит выдан на 2 года под 30% годовых, начисляемых по простой процентной ставке. Оценить реальную доходность данной финансовой операции с точки зрения кредитора. Уровень инфляции равен 25% в год.
| Дано: | Решение: |
 n = 2 года α = 25% = 0,25 ia = 30% = 0,30 n = 2 года α = 25% = 0,25 ia = 30% = 0,30 | |
| i = ? | Ответ: реальная доходность 1,2% годовых, начисляемых по простой процентной ставке. |
Простая учетная ставка с учетом инфляции.
 |
Формула для простой учетной ставки следующая:
|
 |
Учесть инфляцию можно двумя способами:
 |
Пример 4.4. Под какую простую учетную ставку нужно выдать кредит на 6 месяцев, чтобы реальность доходность операции составила 10% при уровне инфляции 20% в год?
Пример 4.5. Ссуда дана по учетной ставке 30% годовых на 6 месяцев. Какова реальная доходность операции с точки зрения кредитора при уровне инфляции 25%?
Сложная процентная ставка с учетом инфляции. Пример 4.6. Кредит в размере 40000 рублей выдан на два года. Реальная доходность должна составить 10% годовых, начисляемых ежеквартально. Ожидаемый уровень инфляции 20% в год. Определить сложную ставку процентов кредита, компенсирующую инфляционные потери, и вычислить наращенную сумму.
Пример 4.7. Определите реальную доходность финансовой операции, если при уровне инфляции 20% в год кредит выдается на 2 года по номинальной ставке сложных процентов в размере 30% годовых при ежеквартальном начислении процентов.
Пример 4.8. Определить, какой реальной доходностью обладает финансовая операция, если при уровне инфляции 20% в год деньги вкладываются на 2 года под 15% годовых при ежемесячном начислении процентов. Источник Начисление процентов по кредитам и депозитамНачисление простой и сложной процентной ставки. Учет векселей с дисконтом. Долговые обязательства по учетной ставке. Реальная доходность финансовой операции банка. Составление плана погашения кредита. Погрешность при вычислении погасительного платежа.
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную нижеСтуденты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны. Размещено на http://www.allbest.ru/ АВТОНОМНАЯ НЕКОММЕРЧЕСКАЯ ОРГАНИЗАЦИЯ ВЛАДИМИРСКИЙ ИНСТИТУТ БИЗНЕСА Балашова Оксана Евгеньевна Форма обучения Дистанционное Факультет Экономики и Финансов Специальность Финансы и кредит Номер зачетной книжки ЗФ-020/10 1. Кредит 9600 руб. выдан 29,07 2001г. под 24 %, начисляемых по простой процентной ставке. Найти возвращаемую сумму, если день погашения кредита 24,02 2002г. Решить задачу, используя Германскую, Британскую и Французскую методики. a) (360/360): К = 360; t = (30?29) + 30 · 6 + 24 = 205; S = 9600 (1 + 0.24 · 205/360) = 10912 (руб.) б) (365/365): К = 365; t= 210; t= 420; t = 420 ? 210 = 210 S = 9600 (1 + 0.24 · 210/366) = 10925.59 (руб.) в) (365/360): К = 360; t = 210; S = 9600 (1 + 0.24 · 210/360) = 7866 (руб.) Ответ: самая выгодная для кредитора Британская методика, возвращаемая сумма — 10925,59 рублей 2. Векселедержатель предъявил для учета вексель на сумму 15000 руб. со сроком погашения 12,08 2004 года. Вексель был предъявлен 25,02 2004 года. Банк согласился учесть вексель с дисконтом в 22 % годовых. Какую сумму получит векселедержатель? P = S (1 — d ) t = t1 — t2= 225 — 56=169 P= 15000(1-0.22* 169/360) = 13450.5 3. Вы владелец векселя на сумму 82000 руб. со сроком погашения 24,05 2006 года. Банк учитывает долговые обязательства по учетной ставке 23 % годовых. Рассчитайте срок учета векселя в банке, если вам нужно получить не меньше 78000 руб. P = S (1 — d ) t = (S — P)•K / (S•d) t = (82000-78000)•360 / (82000•0.23) =76.35 ? 76 (за 76 дня до 24.05 сумма будет меньше 78000) t = 144+366-76 = 434 28 февраля 2007 года 4. Для клиента имеются следующие варианты: а) банк 1 15 % годовых ? начисление процентов по полугодиям б) банк 2 14,4 % годовых ? начисление процентов ежеквартально в) банк 3 14 % годовых ? начисление процентов ежемесячно С помощью эффективной годовой процентной ставки определить самый выгодный вариант для клиента. a) i1 = (1 + 0.15/2)2 — 1 = 0.1556 б) i2 = (1 + 0.144/4)4 — 1 = 0.1519 б) i3 = (1 + 0.14/12)12 — 1 = 0.1493 для вкладов выгоднее первый банк; кредиты выгоднее брать в третьем банке. 5. Банк представил ссуду в размере 65000 рублей на 32 месяцев под 20 % годовых. Проценты начисляются 2 раз в год. Рассчитайте возвращаемую сумму. n = m•N = 32/12 • 4 = 5+0, 33 S = P· (1 + j/m)Є · (1 + b · j/m) S =65000· (1+0.20/2)5· (1+0, 33 · 0.20/2)=108137.69 Ответ: возвращаемая сумма равна 108137.69 6. Банк начисляет 24% годовых по ставке сложных процентов. Клиент сделал первый взнос 9600 рублей — 16,05 2000 года, второй взнос 5200 рублей — 24,07 2001 года, третий взнос 3200 рублей — 27,06 2002 года. Какая сумма будет у клиента на счете 25,10 2004 года. n = a + b; S = P· (1 + j/m) Є · (1 + b · j/m); b = S1 =9600· (1+0.24)5· (1+ 0.24· 162/360) =31183, 11 S2 =5200· (1+0.24)7· (1+0, 24 · 94/360) =24907, 21 S3 =3200· (1+0.24)6· (1+0, 24 · 121/360) =12570, 28 S =31183, 11+24907, 21+12570, 28 =68660, 6 7. За какой срок первоначальный капитал 65000 рублей увеличится до 86000 рублей, если на него будут начисляться 2 раз в год сложные проценты по ставке 27% годовых? N = lg( 86/65)/2lg(1+0.27/2)= 1,1055 (лет) 1,1055 (лет) ? 13(мес.) ? 398(дней) 8. Какова должна быть процентная ставка сложного процента, чтобы первоначальный капитал 24000 рублей возрос до 40000 за 4 лет. Решить эту задачу для случая начисления процентов 2 раз. j = 2 ((40/24) — 1) = 0,1318 = 13.18% 9. Кредит 52000 рублей выдан на 7 месяцев. Какова должна быть простая процентная ставка, если кредитор желает получить 14 % реальной доходности, начисляемых по простой процентной ставке, при уровне инфляции 7 % в год? Вычислить наращенную сумму I= (1 + б)Є · (1 + b · б) I= (1 + 0.7·0.07) = 1.049 i= ((1+0.7·0.14) ·1.049 ? 1) / 0,7 = 0,21686 Sб = 52000· (1+0.7·0.21686) = 59893,704 Ответ: процентная ставка — 21,6%; наращенная сумма — 59893,704 рублей 10. Определите реальную доходность финансовой операции банка, если он при уровне инфляции 13 % в год выдает кредит на 3 лет по номинальной ставке 27 % годовых. Проценты начисляются 4 раз в год. j = (4+0.27) (1 +0.13)? 4 = 0.4024 Реальная доходность 40,24% 11. Вы заняли на 5 лет 45000 рублей под 16 % годовых, начисляемых по схеме сложных процентов на непогашенный остаток. Возвращать нужно равными суммами в конце каждого года. Составить план погашения кредита. 1. Найдем погасительный платеж: процентный ставка дисконт кредит ПЛАН ПОГАШЕНИЯ КРЕДИТА. Сумма долга на начало периода Сумма процентных денег за период Сумма погашенного долга 2. При подсчете процентных денег за последний (5) период получаем: 11817,64 · 0,16 = 1895,63 «Недостающие» копейки — погрешность при вычислении погасительного платежа. Для компенсации погрешности вычислений (не более 0,5 копейки за период) корректируем сумму процентных денег за последний период (1895.81). 3. Сумма погашенного долга за все периоды равна сумме долга на начало первого периода. Сумма всех платежей равна сумме всех процентных денег и сумме погашенного долга. Погрешность вычислений не превышает допустимую (0.5 • 4 = 2) Следовательно, план погашения кредита составлен, верно. 12. Фирме нужно накопить 92000 рублей, чтобы через 5 лет заменить часть устаревшего оборудования. Каковы должны быть отчисления, совершаемые 2 раз в год. Банк начисляет 14 % также 2 раз в год. S=92000(1+0,14) 10 = 341064,36 Лист проверки (заполняется преподавателем) Размещено на Allbest.ru Подобные документыОпределение суммы процента за кредит при германской и английской практике. Начисление процентов за кредит, погашенный единовременным платежом. Расчет ставки процентов по кредиту с учетом инфляции. Доходность вкладов по годовой ставке сложных процентов. задача [19,5 K], добавлен 14.11.2009 Методика определения суммы платежа с применением ставки сложных процентов. Расчет доходности операции для кредитора в виде простой, сложной процентной и учетной ставки. Вычисление предпочтительного варианта вложения денег при заданных процентных ставках. контрольная работа [38,1 K], добавлен 26.03.2013 Начисление простых процентов. Наращенная сумма с учетом инфляции. Создание фонда развития фирмы. Вложение инвестиций. Чистый приведённый доход проекта и индексы доходности и прибыльности. Составление плана погашения кредита и начисления процентов. контрольная работа [30,4 K], добавлен 21.03.2009 Определение вексельной суммы, процентной ставки, эквивалентной банковской учетной ставке. Расчет реальной годовой доходности по облигациям при заданных номинальной процентной ставке и уровне инфляции. Ожидаемая реальная доходность держателя векселя. контрольная работа [26,4 K], добавлен 21.12.2012 Расчет суммы выплаты по векселю при простой учетной ставке. Составление плана погашения кредита равными суммами (аннуитетами). Определение средних размеров коммерческого кредита, срока пользования ссудами при условии их непрерывной оборачиваемости. контрольная работа [16,3 K], добавлен 17.12.2013 Определение размера погасительного платежа при начислении процентов по простым, сложным процентным и учетным ставкам. Методы расчета ссуды по простым фиксированным процентным ставкам. Математическое дисконтирование при простой процентной ставке. контрольная работа [27,9 K], добавлен 17.03.2014 Вычисление эффективной ставки процента. Определение цены кредита в виде простой годовой учетной ставки и годовой ставки простых процентов, множителя наращения за весь срок договора, процента и суммы накопленного долга, доходности операции для кредита. контрольная работа [27,6 K], добавлен 21.12.2013 Источник |



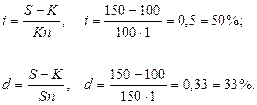
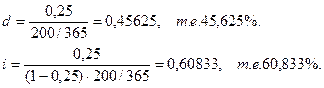
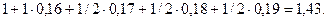
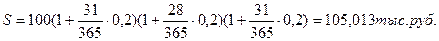
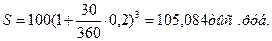
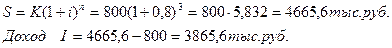
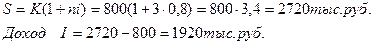

 n = 0,5 лет α = 20% = 0,20 d = 10% = 0,10
n = 0,5 лет α = 20% = 0,20 d = 10% = 0,10 n = 0,5 лет α = 25% = 0,25 da = 30% = 0,30
n = 0,5 лет α = 25% = 0,25 da = 30% = 0,30 P = 40000 руб.
P = 40000 руб. n = 2 года jα = 30% = 0,30 a = 20% = 0,20 m = 4
n = 2 года jα = 30% = 0,30 a = 20% = 0,20 m = 4