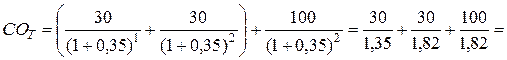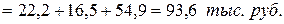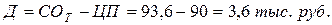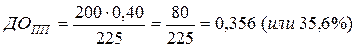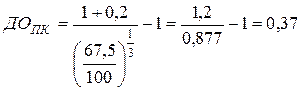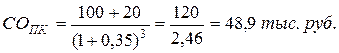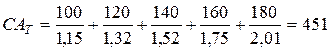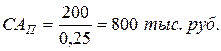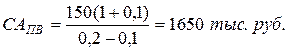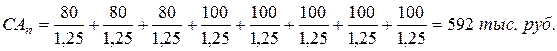Ожидаемая доходность акций
В сфере инвестирования ожидаемая доходность (англ. Expected Rate of Return) представляет собой процентную ставку или сумму, которую инвестор ожидает получить в течение определенного периода времени от вложений в определенный актив. С практической точки зрения этот показатель может быть рассчитан исходя из полного набора вероятностей, либо на основе исторических данных о доходности актива.
Формула
В случае, если заранее известен полный набор вероятностей, то есть вероятности всех возможных вариантов исхода событий, ожидаемую доходность можно рассчитать использовав следующую формулу:

где Pi – вероятность наступления i-го исхода событий;
ki – доходность при i-ом исходе событий;
n – количество исходов событий.
В условиях реального финансового рынка инвестор, как правило, принимает решение на основании имеющейся информации об исторической доходности ценной бумаги. В этом случае ожидаемая доходность рассчитывается как среднеарифметическое:

ki – доходность ценной бумаги в i-ом периоде;
n – количество наблюдений.
Пример расчета
Пример 1. Финансовый аналитик рассматривает возможность включения в портфель инвестора одной дополнительной акции, выбирая из трех компаний, работающих в сфере оптово-розничной торговли. При этом он рассматривает три возможных сценария развития событий, вероятность и предполагаемая доходность которых представлены в таблице.
Чтобы определить ожидаемую доходность каждой из ценных бумаг, необходимо воспользоваться первой из приведенных выше формулой. Для акций Компании А она составит 11,25%, акций Компании Б 12,4% и акций Компании В 12,9%.



Если не принимать во внимание прочие факторы (например, риск), то в портфель инвестора целесообразно включить акции Компании В, поскольку они характеризуются самой высокой ожидаемой доходностью.
Пример 2. Финансовому аналитику необходимо оценить ожидаемую доходность акций на основании данных об их исторической доходности за последние 7 недель, которые представлены в таблице.
Поскольку аналитику известна только историческая доходность акций, необходимо воспользоваться второй из приведенных выше формул.



Источник
Определить ожидаемую текущую норму доходности

Как рассчитать внутреннюю норму доходности
С помощью расчёта внутренней нормы доходности (ВНД) можно узнать, стоит ли инвестировать в проект. Объясняем, как рассчитать и использовать этот финансовый показатель.
Что такое ВНД
Предположим, вы хотите вложить средства в бизнес-проект, который в будущем должен принести деньги. Чтобы понять, насколько это выгодно, нужно из предполагаемого дохода вычесть сумму начальных инвестиций.
Казалось бы, всё просто. Но есть нюанс: 1000 рублей сегодня и 1000 рублей через год — неравнозначные суммы, потому что деньги имеют свойство дешеветь. В связи с этим для оценки будущего дохода от инвестиций в расчётах используют ставку дисконтирования.
Ставка дисконтирования — это процент, отражающий соотношение будущего дохода и его нынешней стоимости. При определении этого показателя учитывают все риски бизнес-проекта, включая инфляцию, обострение политической ситуации, ошибки менеджмента и т. д. Чем выше риски, тем выше процент, на который «сгорят» деньги инвестора через какое-то время.
Источник
Внутренняя норма доходности инвестиционных проектов
Поэтому разрабатываются и используются инструменты, позволяющие провести первичный расчёт рисков и, в некоторой степени, минимизировать вероятность вложения средств в низкодоходные или убыточные проекты.
Чаще всего при выполнении финансового анализа используется показатель, оперирующий приведёнными денежными потоками. Его именуют внутренняя ставка доходности (иное обозначение, норма доходности (международное обозначение, IRR).
Внутренняя норма доходности инвестиционного проекта IRR (Internal Rate of Return) — это величина ставки дисконта, достигая которой совокупная приведенная стоимость вложений в проект, именуемая денежными потоками либо чистой приведенной стоимостью (обозначается как «NPV») равна «0». Говоря простым языком, при такой ставке инвестор, вкладывающий в проект собственные средства, сможет, в лучшем случае, их возместить.
Говоря простым языком, при такой ставке инвестор, вкладывающий в проект собственные средства, сможет, в лучшем случае, их возместить.
Выполняя финансовый анализ проекта сначала считают показатель NPV (приводят величину общей суммы инвестиций к стоимости «на сегодня»). Только после этого определяют величину ставки IRR инвестиционного проекта. Этот показатель может именоваться по-разному (но, в любом случае, в наименовании первым словом будет «внутренняя»):
- внутренней нормой дисконта;
- внутренним коэффициентом эффективности (вариант, окупаемости);
- внутренней нормой.
Внутренняя норма доходности, вместе с величиной NPV, рассматриваются как взаимодополняющие критерии, позволяющие оценить эффективность реализации инвестпроекта. Графическая зависимость между ними приведена на рисунке.
Рассчитанную величину IRR рассматриваемого проекта сопоставляют с аналогичными значениями рыночной ставки доходности (на момент сравнения). При этом обязательно дополнительно учитываются такие факторы, как сроки реализации проекта и возможные риски.
В качестве контрольной величины используется ставка усреднённого банковского депозита. Рентабельным будет считаться проект, имеющий величину внутренней нормы доходности, превышающую средние величины ставок по инвестпроектам (вариант, по вкладам).
Необходимость рассчитать величину ставки ВНД возникает при различных направлениях денежных потоков:
- Эти показатели, в первом случае, рассматриваются исключительно как чистые инвестиции. На начальной стадии реализации любого проекта все они минусовые (инвестор вкладывает, но ничего не получает). Спустя определённое время появляются потоки положительной направленности. На весь оставшийся период реализации рассматриваемого проекта динамика не меняется.
- Во втором учитываются показатели, характеризующие смешанные денежные потоки. Средства поступают, чередуясь положительной и отрицательной направленностью. В подобных случаях показатель IRR не используется, так как он не позволяет получить достоверных данных. Необходимо обращаться к модифицированному показателю, MIRR.
Присоединяйтесь к более 3 тыс. наших подписчиков. 1 раз в месяц мы будем отправлять на ваш email дайджест лучших материалов, опубликованных у нас на сайте, на странице в LinkedIn и Facebook.
Источник
Модели оценки реальной стоимости и ожидаемой доходности фондовых инструментов



С учётом особенностей формирования денежного потока и дифференциации нормы текущей доходности рассмотрим модели оценки реальной стоимости отдельных фондовых инструментов.
Оценка облигаций (сберегательных сертификатов и других аналогичных ценных бумаг) предусматривает решение ряда задач, среди которых важнейшей является определение её текучей рыночной стоимости.
Формула, по которой рассчитывается этот показатель, называется «Основной моделью оценки облигаций» (Basic Bond Valuation Model).
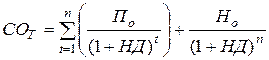
где: СОТ – текущая рыночная стоимость облигации;
По – ежегодная сумма процента по облигации, представляющая собой произведение её номинала на объявленную ставку процента:
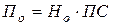
Если сумма процента выплачивается с иной периодичностью (например, раз в полугодие, раз в квартал и т.п.), то расчет по формуле производится с предусматриваемыми периодами выплаты процента;
Но –номинал облигации, подлежащей погашению в конце периода её обращения;
ПС – ставка, по которой будет начислена сумма процента по облигации, в десятичной дроби;
НД – норма текущей доходности, используемая как дисконтная ставка в расчётах настоящей стоимости, в десятичной дроби;
n – число лет (или иных периодов), остающихся до погашения облигации.
Пример: На фондовом рынке предлагается к продаже облигация одной из компаний по цене 90 тыс. руб. за единицу. Она была выпущена сроком на 3 года, до погашения осталось 2 года. Её номинал при выпуске – 100 тыс. руб. Процентные выплаты по облигации осуществляются 1 раз в год по ставке 30 % к номиналу. С учётом уровня риска данного типа облигации норма её текущей доходности – 35 % в год. Определить текущую рыночную стоимость облигации и её соответствие цене продажи (ЦП).
НД = 0,35______
Д – дополнительный доход в связи с заниженной рыночной стоимостью.
I. 1.1. Модель расчёта ожидаемой доходности по облигациям без выплаты процентов
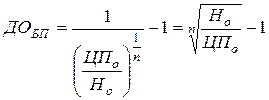
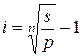
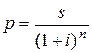
где: ДОБП – ожидаемая доходность по облигации без выплаты процентов, в десятичной дроби;
Но – номинал облигации, подлежащий погашению в конце периода её обращения ;
ЦПо – цена, по которой облигация реализуется на рынке;
n – число лет (или иных периодов), отстающих до погашения облигации.
Экономическое содержание данной модели состоит в том, что уровень ожидаемой доходности по облигациям без выплаты процентов представляет собой дисконтную ставку, по которой номинал облигации приводится к настоящей стоимости, приравненной к цене её реализации.
Пример: Облигация внутреннего местного займа номиналом в 100 тыс. руб. реализуется по цене 67,5 тыс. руб. Погашение облигации предусмотрено
через 3 года. Норма текущей доходности по облигациям такого типа составляет 16 %. Определить ожидаемую доходность по облигации и её соответствие текущей норме доходности облигаций такого типа.
НД = 0,16
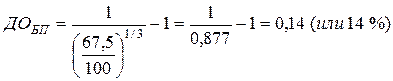
НД — ДОБП = 0,16 – 0,14 = 0,02 уровень доходности ниже среднерыночной на 2 % Þ невыгодна.
1.2. Модель расчёта текущей рыночной стоимости облигаций без выплаты процентов.
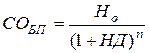
где: СОБП – текущая рыночная стоимость облигаций без выплаты процентов;
Но – номинал облигации, подлежащий погашению в конце периода её обращения;
НД – норма текущей доходности по конкретному виду облигаций (в десятичной дроби);
n – число лет (или иных периодов), остающихся до погашения облигации.
Пример: Определить текущую рыночную стоимость облигации внутреннего местного займа и сопоставить её с ценой продажи, используя данные предыдущего примера.
ЦП – СОБП = 67,5 – 64,1 = 3,4 тыс. руб. Þ цена завышена на 3,4 тыс. руб. Þ невыгодна.
2.1. Модель расчёта ожидаемой текущей доходности по облигациям с периодической выплатой процентов.
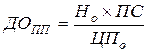
где: ДОПП – ожидаемая текущая доходность по облигации с периодической выплатой процентов, в десятичной дроби;

Но – номинал облигации, к которому начисляется сумма процента;
ПС – ставка, по которой начисляется сумма процента по облигации, в десятичной дроби;
ЦПо – цена, по которой облигация реализуется на рынке.
Необходимость дисконтирования в этом случае отпадает, т.к. оба указанных показателя должны приводиться к настоящей стоимости по единой ставке дисконта, в результате чего их соотношение не изменится.
При расчёте текущей рыночной стоимости таких облигаций используется Основная модель оценки облигаций.
Пример. Облигация компании номиналом Но = 200 тыс. руб. реализуется на рынке по цене ЦПо = 225 тыс. руб. Става ежегодного начисления процентов по ней (купонная ставка). ПС = 0,40. Норма текущей доходности по облигациям такого типа НД = 0,35. Определить ожидаемую текущую доходность по облигации, сопоставив её с нормой текущей доходности.
ДОПП – НД = 0,356 – 0,35 = 0,006 (на 0,6 % превышает нормативную) Þ выгодна.
3.1. Модель расчёта ожидаемой текущей доходности по облигациям с выплатой всей суммы процентов при погашении.
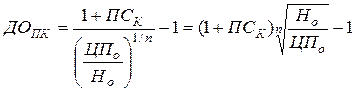
где: ДОПК – ожидаемая текущая доходность по облигации с выплатой всей суммы процентов при погашении, в десятичной дроби;
ЦПо – цена, по которой облигация реализуется на рынке;
Но – номинал облигации, к которому при погашении будет начислена сумма процента;
ПСК – ставка, по которой будет начислена сумма процента по облигации при её погашении, в десятичной дроби.
3.2. Модель расчёта текущей рыночной стоимости облигаций с выплатой всей суммы процентов при погашении.
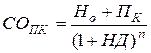
где: СОПК – текущая рыночная стоимость облигации с выплатой всей суммы процентов при погашении;
Но – номинал облигации, подлежащей погашению в конце периода её обращения;
ПК – сумма процента по облигации, которая будет начислена при её погашении по соответствующей ставке;
НД – норма текущей доходности, используемая как дисконтная ставка в расчётах настоящей стоимости, в десятичной дроби;
n – число лет (или иных периодов;, остающихся до погашения облигации.
Пример. Облигация компании номиналом Но = 100 тыс. руб. реализуется на рынке по цене ЦПо = 67,5 тыс. руб. Погашение облигации и разовая выплата суммы процента по ней по ставке ПСК = 20 % предусмотрены через n = 3 года. Норма текущей доходности по облигациям такого типа НД = 0,35. Определить ожидаемую текущую доходность и текущую рыночную стоимость данной облигации.
ЦПо – СОПК = 67,5 – 48,9 = 18,6 тыс. руб. (цена продажи завышена на 18,6 тыс. руб.) Þ невыгодна.
ДОПК – НД = 37 %- 35 % = 2 % — на 2 % выше среднерыночной Þ выгодна.
Вышеперечисленные методы оценки облигаций полностью применимы к расчёту аналогичных показателей по сберегательным сертификатам и другим кредитным ценным бумагам.
Оценка акций направлена прежде всего на определение их текущей рыночной стоимости. Особенно актуальна эта задача в условиях фондового рынка, где рыночная цена продажи акций многих предприятий и банков значительно превышает их реальную текущую рыночную стоимость.
1) Модель оценки текущей рыночной стоимости акции при её использовании в течение неопределённого продолжительного периода времени.
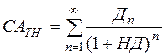
где: САТН – текущая рыночная стоимость акции, используемой неопределённое число лет;
Дn – сумма дивидендов, которую инвестор ожидает получить в n-ом году;
НД – норма текущей доходности акций данного типа, используемая как дисконтная ставка в расчётах настоящей стоимости, в десятичной дроби;
n – число лет, включённых в расчёт.
Пример. Приобретенная инвестором акция представляется инвестору перспективной и намечена им к использованию в течение продолжительного периода. На ближайшие пять лет им составлен прогноз дивидендов, в соответствии с которым в первый год сумма дивидендов составит 100 тыс. руб., а в последующие годы будет ежегодно возрастать на 20 тыс. руб. Норма текущей доходности акций данного типа составляет 15 % в год. Определить текущую рыночную стоимость акции.
2) Модель оценки текущей рыночной стоимости акций при их использовании в течение заранее предусмотренного срока:
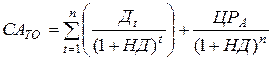
где: САТО – текущая рыночная стоимость акции, используемой в заранее предусмотренный период;
Дt – сумма дивидендов, которую инвестор ожидает получить в t-ом году;
ЦРА – прогнозируемая рыночная цена реализации акции в конце периода её использования;
НД – норма текущей доходности акций данного типа, используемая как дисконтная ставка в расчётах настоящей стоимости, в десятичной дроби;
n –число лет использования акции.
Экономическое содержание данной модели аналогично Основной модели оценки облигаций.
3) Модель оценки текущей рыночной стоимости акций с постоянными дивидендами:
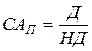
где: САП – текущая рыночная стоимость акции с постоянными дивидендами;
Д – годовая сумма постоянного дивиденда;
НД – норма текущей доходности акций данного типа, в десятичной дроби.
Пример. По акции выплачивается ежегодный постоянный дивиденд в сумме Д = 200 тыс. руб. Норма текущей доходности акций данного типа составляет 25 % в год. Найти текущую рыночную стоимость акции.
4) Модель оценки текущей рыночной стоимости акций с постоянно возрастающими дивидендами («модель Гордона»).
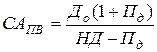
где: САПВ – текущая рыночная стоимость акции с постоянно возрастающими дивидендами;
До – сумма последнего уплаченного дивиденда;
НД – норма текущей доходности акций данного типа, в десятичной дроби;
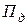
Пример. Последний дивиденд, выплаченный по акции, составлял До=150 тыс. руб. Компания постоянно увеличивает сумму ежегодно выплачиваемых дивидендов на 10 %. Норма текущей доходности акций данного типа – 20 % в год. Найти текущую рыночную стоимость акции. САПВ — ?
5) Модель оценки текущей рыночной стоимости акций с изменяемой суммой дивидендов по периодам.
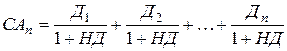
где: САn – текущая рыночная стоимость акции с изменяемой суммой дивидендов;
Дn – сумма дивидендов, прогнозируемая в n-ом периоде;
НД – норма текущей доходности акций данного типа, в десятичной дроби;
n – число прогнозируемых лет.
Пример. В соответствии с принятой дивидендной политикой компания ограничила выплату дивидендов в предстоящие три года суммой 80 тыс. руб. в год. В последующие пять лет она обязалась выплачивать постоянные дивиденды в размере 100 тыс. руб. в год. Норма текущей доходности акций данного типа составляет 25 % в год. Текущая рыночная стоимость акций составит:
Модели оценки реальной рыночной стоимости и текущей доходности отдельных фондовых инструментов используются при их выборе и включении в формируемый инвестиционный портфель.
Источник