Определить npv irr срок окупаемости для денежного потока

Инвестиционные показатели NPV, IRR: Excel на службе у финансового директора

Как рассчитать NPV и IRR, оценить эффективность инвестиционных проектов, рассчитать сумму аннуитета и проверить банк на честность. Финансовых формул в Excel много. Часть из них предназначена для расчета амортизации разными способами. Другие – для определения стоимости ценных бумаг. Третьи для чего-то еще. Здесь мы разберем самые главные и «животрепещущие» (на мой взгляд).

Это формулы, которые позволят рассчитать:
— NPV (Net Present Value) — чистую приведенную стоимость.
— IRR (Internal Rate of Return) — внутреннюю ставку доходности.
— Аннуитеты – равномерные платежи.

Также рассмотрим некоторые нюансы использования этих формул. Все расчеты можно найти в приложенном файле. Основной акцент сделан на функции Excel, поэтому саму финансовую математику разбирать особо не будем.

Оценка целесообразности проекта с помощью NPV

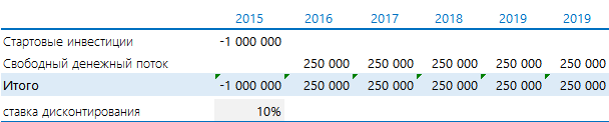
Есть проект, который ежегодно в течении 5 лет будет приносить 250 000 руб. Нужно потратить 1 000 000 руб. Предположим, что ставка дисконтирования равна 10%.

Оцениваем NPV проекта. Напомню формулу этого показателя:

Если денежные потоки, приведенные к текущему периоду, больше инвестированных денег (NPV > 0), то проект выгодный. В противном случае – нет. Другими словами, нам потребуется сделать в Excel следующее:

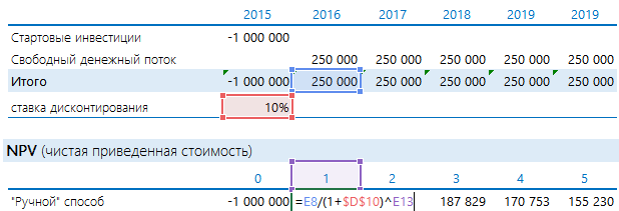
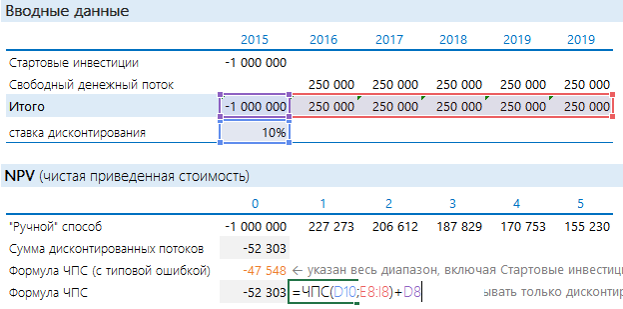
Добавить порядковые номера лет: 0 – стартовый год, к нему приводятся потоки. 1, 2, 3 и т.д. – это годы реализации проекта. В формуле на рисунке выполнены действия, которые прописаны выше после знака суммы (Σ): денежный поток за период делится на сумму 1 и ставки дисконтирования, возведенную в степень соответствующего года.

Рассчитанная строка представляет собой дисконтированный денежный поток. Чтобы получить значение NPV, достаточно найти общую сумму всей строки.

Получается «-52 303». Проект невыгоден.

Чтобы определить NPV, на самом деле необязательно готовить такую таблицу. Достаточно воспользоваться формулой Excel ЧПС. Синтаксис формулы такой (здесь и далее будет написано не как в справке Excel, а в переводе на понятный язык):

ЧПС(Ставка дисконтирования; Диапазон дисконтируемых значений)

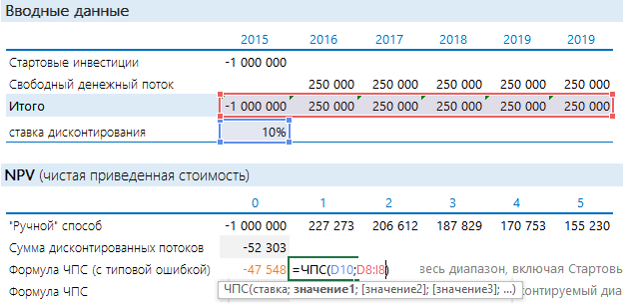
То есть достаточно указать ячейку с процентом и с денежными потоками. Но при использовании этой формулы с непривычки финансисты часто допускают ошибку:

Вообще-то дисконтированный поток и расчет по ЧПС должны совпадать. Почему же здесь разные значения? Дело в том, что ЧПС начинает дисконтировать с первого же значения. Т.е. она на самом деле ищет приведенную стоимость. А стартовые инвестиции нужно отнимать после. Правильная запись формулы в нашем случае будет иметь следующий вид:

Стартовые инвестиции «выведены» за пределы дисконтируемого диапазона и вычтены: т.к. стартовые инвестиции уже идут с минусом, то D8 нужно прибавлять. Теперь результаты одинаковые.

Оценка целесообразности проекта с помощью IRR

Как еще можно оценить проект? Можно посмотреть на него с точки зрения ставки дисконтирования. Задать вопрос: а какая должна быть ставка, чтобы NPV стала = 0? Вот этой ставкой как раз и является IRR. Если Ставка дисконтирования
Аннуитеты – любимая банковская цифра

Сначала поговорим о волнующем вопросе – как банки рассчитывают сумму равномерного платежа, как их проверить и как это понимать. Допустим, вы собираетесь взять кредит 1 000 000 руб. на 5 лет под 10% годовых. Платить будете раз в год равными платежами. Формулу из учебника по финансовому менеджменту здесь приводить не будем. Приведем формулу Excel:

ПЛТ(Ставка дисконтир; Количество периодов; Сумма кредита которую вы берете)

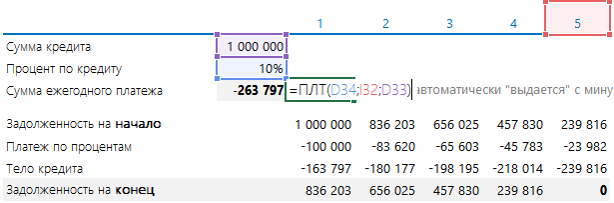
В формуле есть еще два необязательных пункта: сумма, которая должна остаться (по умолчанию ноль), и как высчитывать сумму – на начало месяца, и тогда ставят 1, или на конец – ставят ноль. В 90% случаев эти пункты не нужны, поэтому их можно не ставить вообще. Итого аннуитет определяется так:

Сумма ежегодного платежа получается сразу с минусом. Эту сумму нужно каждый год платить банку.

В ней содержатся две части: 1) платеж по кредиту, 2) тело кредита.

Ниже они показаны. Платеж по кредиту берется как 10% (процент по кредиту) от суммы задолженности на начало периода. Тело – как разность между ежегодным платежом и платежом по процентам (в Excel можно найти формулы, которые рассчитают вам и эти платежи). Задолженность на конец рассчитывается как разность между Задолженностью на начало и платежом по телу кредита.

Если платежи не ежегодные, а ежемесячные или ежеквартальные, то нужно ставку и период приводить к этим значениям. Так если бы у нас платеж был каждый месяц, формула выглядела бы так:

Мы бы годовую ставку разделили на 12 (привели к ежемесячному), и взяли не 5 периодов, а 5 • 12 = 60 месяцев. И получили ежемесячный платеж в 21 247 руб.

Нюансы и тонкости

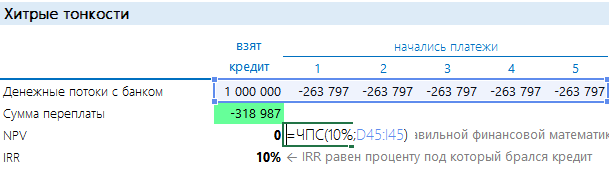
А теперь обсудим, как проверять банки на честность. Любой поток платежей по кредиту подразумевает под собой, что все выбытия денег приведены к поступлениям на ставку кредитования. Теперь по-русски: если мы построим денежный поток из полученного нами кредита и последующих наших аннуитетных платежей, то затем мы можем посчитать по ним NPV и IRR. NPV при этом должно принять нулевое значение, а IRR, что интереснее, — показать нам реальную процентную ставку.

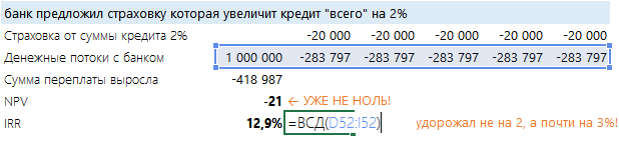
Когда кредит и платежи по нему рассчитаны правильно, то NPV, взятый по той же процентной ставке, равен нулю. А IRR показывает ставку. Когда банк делает предложение, от которого невозможно отказаться и которое увеличит кредитную ставку «всего» на несколько процентов – не верьте и пересчитывайте! Например, в нашем случае банк предложил страховку «всего» 2 % от суммы кредита в год. Думаете это прирост всего в 2%? Нет! Дело в том, что настоящий кредит в начале каждого года уменьшается:

В результате видно, что NPV не равен нулю. А реальный процент не 10, а 12,9%! Обратите внимание: здесь же выросла сумма переплаты. Если вас это смутит, вам могут предложить «еще более выгодные условия» — заплатить переплату сейчас, а остальное потом, меньшими платежами, или в нашем примере просто заплатить больше, а потом меньше. Сумма переплаты не изменится, а вот процент…

Что здесь сделано? Из каждого последующего платежа взята сумма 43 797 руб. и добавлена к первому же платежу (а бывает выкручивают сумму в момент выдачи кредита). Если для реального сектора финансовая математика «деньги вчера – деньги завтра» кажется несколько отдаленной от жизни, для банков это реальная прибыль. Поэтому всеми силами нагружают первый платеж. А вы с помощью простых формул сможете подготовить основу для дальнейших переговоров.

Да, не забудьте, если речь идет про ежемесячные платежи, умножать на 12.

Источник

Оценим инвестиционный проект

Задача по экономике:

Расчет NPV, PI, срока окупаемости простого, срока окупаемости дисконтированного, индекса рентабельности инвестиций, внутренней нормы доходности.

Дано: Инвестиции в бизнес составили 500 тыс. рублей.

Ожидаемые доходы (CFi) за 5 лет составят:

2014 год – 100 тыс. рублей. 2015 год – 150 тыс. рублей.

2016 год – 200 тыс. рублей. 2017 год – 250 тыс. рублей.

2018 год – 300 тыс. рублей.

Ставка дисконтирования 20%.

1. чистый дисконтированный доход (NPV) за 5 лет,

2. индекс прибыльности (PI) ,

3. сроки окупаемости простой и дисконтированный,

4. внутреннюю норму доходности (IRR).

Сначала рассчитаем чистые денежные потоки по формуле CFi/(1+r) t

Где CFi – денежные потоки по годам.

r – ставка дисконтирования.

t – номер года по счету.

Тогда в первый год чистый денежный поток будет равен CFi/(1+r) t = 100000 /(1+0,2) 1 =83333,33 рублей.

Во второй год чистый денежный поток будет равен CFi/(1+r) t = 150000 /(1+0,2) 2 = 104166,67 рублей.

В третий год чистый денежный поток будет равен CFi/(1+r) t = 200000 /(1+0,2) 3 = 115740,74 рублей.

В четвертый год чистый денежный поток будет равен CFi/(1+r) t = 250000 /(1+0,2) 4 = 120563,27 рублей.

В пятый год чистый денежный поток будет равен CFi/(1+r) t = 300000 /(1+0,2) 5 = 120563,27 рублей.

Где I – сумма инвестиций.

∑CF_i/(1+r) i – сумма чистых денежных потоков.

∑CF_i/(1+r) i =83333,33+104166,67+115740,74+120563,27+120563,27 =544367,28 рублей.

NPV=83333,33+104166,67+115740,74+120563,27+120563,27 – 500000 = 44367,28 рублей.

NPV= 44367,28 рублей.

NPV должен быть положительным, иначе инвестиции не оправдаются. В нашем случае NPV положителен.

Рассчитаем индекс рентабельности PI (profitability index).

Индекс рентабельности рассчитывается по формуле:

(чистые денежные потоки делим на размер инвестиций).

Тогда индекс рентабельности будет = 544367,28 / 500000=1,09.

Если индекс рентабельности инвестиций больше 1, то можно говорить о том, что проект эффективен.

Обобщим данные расчета NPV в таблице.

Рассчитаем срок окупаемости простой.

Инвестиции 500000 рублей.

В первый год доход 100000 рублей, т.е. инвестиции не окупятся.

Во второй год доход 150000 рублей, т.е. за два года доходы составили 250000 рублей, что меньше суммы инвестиций.

В третий год доход 200000 рублей, т.е. за три года доходы составили 250000+200000=450000 рублей, что меньше суммы инвестиций.

В четвертый год доход 250000 рублей, т.е. за четыре года доходы составили 450000+250000=700000 рублей, что больше суммы инвестиций.

Т.е. срок окупаемости простой будет 3 с чем-то года. Найдем точное значение по формуле.

Срок окупаемости простой =3+(остаток долга инвестору на конец третьего года) / денежный поток за четвертый год.

Срок окупаемости простой = 3+50000 /250000=3,2 года.

Рассчитаем срок окупаемости дисконтированный.

Инвестиции 500000 рублей.

В первый год чистый денежный поток 83333,33 рублей, т.е. инвестиции не окупятся.

Во второй год чистый денежный поток 104166,67 рублей, т.е. за два года дисконтированные доходы составили 83333,33+104166,67=187500 рублей, что меньше суммы инвестиций.

В третий год чистый денежный поток 115740,74 рублей, т.е. за три года дисконтированные доходы составили 187500+115740,74=303240,74 рублей, что меньше суммы инвестиций.

В четвертый год чистый денежный поток 120563,27 рублей, т.е. за четыре года дисконтированные доходы составили 303240,74+120563,27=423804,01 рублей, что меньше суммы инвестиций.

В пятый год чистый денежный поток 120563,27 рублей, т.е. за 5 лет дисконтированные доходы составили 303240,74+120563,27=544367,28 рублей, что больше суммы инвестиций.

Т.е. срок окупаемости дисконтированный будет больше 4, но меньше 5 лет. Найдем точное значение по формуле.

Срок окупаемости дисконтированный =4+(остаток долга инвестору на конец четвертого года) / чистый денежный поток за пятый год.

Срок окупаемости простой = 4+76195,99 / 120563,27 = 4 , 63 года.

Рассчитаем внутреннюю норму доходности.

Внутренняя норма доходности – это значение ставки дисконтирования, при которой NPV=0 .

Можно найти внутреннюю норму доходности методом подбора. В начале можно принять ставку дисконтирования, при которой NPV будет положительным, а затем ставку, при которой, NPV будет отрицательным, а затем найти усредненное значение, когда NPV будет равно 0.

Мы уже посчитали NPV для ставки дисконтирования, равной 20%. В этом случае NPV = 44367,28 рублей.

Теперь примем ставку дисконтирования равной 25% и рассчитаем NPV.

NPV= 100000/(1+0,25) 1 +150000/(1+0,25) 2 +200000/(1+0,25) 3 + 250000 / (1+0,25) 4 + 300000 / (1+0,25) 5 — 500000= -20896 рублей.

Итак, при ставке 20% NPV положителен, а при ставке 25% отрицателен. Значит внутренняя норма доходности IRR будет в пределах 20-25%.

Внутренняя норма доходности. Расчет

Найдем внутреннюю норму доходности IRR по формуле:

Данный пример предназначен для практических занятий. к.э.н., доцент Одинцова Е.В.

Источник

Оценка инвестиционной эффективности проекта: PBP, NPV, IRR

Для привлечения финансирования бизнеса необходимо предоставить потенциальным инвесторам или кредиторам оценку инвестиционной эффективности проекта или бизнес-плана в виде расчетов соответствующих коэффициентов, чтобы они могли провести сравнительный анализ и выбрать наиболее оптимальный из всех вариантов вложения средств.

Несмотря на то, что уже давно существуют встроенные функции Excel для расчета основных целевых показателей оценки эффективности инвестиций и специализированные программы с графической и табличной информацией, любому специалисту по корпоративным финансам и финансовому директору обязательно понимать суть ключевых методов и показателей инвестиционной оценки, чтобы иметь максимально соответствовать ожиданиям потенциальных кредиторов.

Поэтому в этой статье мы постараемся максимально доступно изложить основные особенности ключевых коэффициентов оценки эффективности инвестиций .

Следует отметить, что процесс принятия решения об инвестировании в тот или иной проект не сводится только лишь к оценке его рентабельности и окупаемости с помощью коэффициентов эффективности. Безусловно во внимание принимаются и такие факторы, как юридические, организационные и технологические аспекты проекта, присущие ему финансовые и специфические риски и возможности их хеджирования и т.д.

Итак, для того чтобы ответить на вопрос, является ли инвестиционный проект достаточно прибыльным для инвестора, традиционно применяется метод дисконтированныя денежных потоков проекта, в основе которого лежит расчет коэффициента дисконтирования (подробнее о нем читайте тут ), характеризующего изменение стоимости денег во времени.

Суть метода дисконта основывается на концепции временной стоимости денег. При таком подходе инвестиции признаются эффективными, если текущая стоимость потенциального генерируемого денежного потока при реализации проекта ( CF1, CF2, … , CFn ) покрывает размер исходной суммы капитальных вложений ( CF0 ) и обеспечивает требуемую отдачу на вложенный капитал (т.е. доходность вложений превышает ставку дисконта, учитывающую все риски с учетом возможных допущений).

В результате применения этого подхода рассчитываются такие стандартные показатели, как:

• дисконтированный срок окупаемости (англ. Pay-Back Period, PBP );
• чистая текущая стоимость (англ. Net Present Value, NPV );
• внутренняянормарентабельности (англ. Internal Rate of Return, IRR ).

Существуют ситуации, когда применение этих показателей неудобно или невозможно, однако в большинстве случаев именно этот набор приводится в резюме каждого бизнес-плана инвестиционного проекта. Такая «универсальность» обусловлена тем, что базой для расчета всех этих показателей служат чистые денежные потоки (англ. Net Cash Flow, NCF ), которые в первую очередь и интересуют потенциальных инвесторов.

Несмотря на то, что как правило одновременно рассчитываются все три показателя, выбор одного из них, который будет являться решающим, зависит от того, какой из двух вариантов задач ставится перед инвестором:

• принять или отклонить конкретный проект, или
• какой проект принять из нескольких альтернативных.

Например, метод дисконтированного периода окупаемости наиболее оптимален при анализе двух взаимоисключающих друг друга проектов (т.е. лучше тот проект, который имеет меньший дисконтированный период окупаемости), а методы NPV и IRR наиболее эффективны при анализе соответствия параметров конкретного проекта критериям отбора.

Следует также знать, что принятие решения об инвестировании не может быть обоснованы лишь одним расчетным показателем. Например, существенным недостатком метода дисконтированного периода окупаемости является то, что он учитывает только начальные денежные потоки, которые укладываются в период окупаемости. Для того чтобы учесть все последующие денежные потоки в расчетах, необходимо, например, рассчитать NPV проекта, чтобы убедиться в том, что за пределами периода окупаемости утвержденный проект обеспечит возврат вложенных инвестиций (для этого NPV должен быть больше или хотя бы равен 0 ). При отрицательном NPV исходная инвестиция не окупается, т.е. положительные денежные потоки, которые генерируются этой инвестицией не достаточны для компенсации, с учетом стоимости денег во времени, исходной суммы капитальных вложений.

Существуют и иные статистические показатели, которые вместо чистых денежных потоков в качестве базы для расчетов используют, например, чистую прибыль рентабельность инвестиционного проекта — ARR, Accounting Rate of Return , или индекс прибыльности — PI, Profitability index ), однако их использование менее распространено.

NPV — метод

Метод NPV основан на расчете суммы текущей стоимости будущих денежных потоков ( CF1, CF2, … , CFn ) и ее сложения с размером первоначальных инвестиций в проект ( CF0 ). Поскольку первоначальные вложения представляют собой отток денежных средств и имеют отрицательное значение, то если суммирование текущей стоимости первоначального (отрицательного) и будущих денежных потоков дает положительный результат (больше 0), то проект принимается к дальнейшему рассмотрению.

Источник