Определить номинальную процентную ставку через годовую доходность

Решение типовых примеров. Пример 1: определить номинальную ставку процентов, которая обеспечивала бы годовую доходность в 26 %

Пример 1: определить номинальную ставку процентов, которая обеспечивала бы годовую доходность в 26 %, если начисление процентов происходит ежемесячно (проценты сложные).

Решение:из формулы (5.3) получим »0,23, или 23 %.

Пример 2: для номинальной ставки 20 % с начислением процентов 2 раза в год найдите эквивалентную ставку, проценты по которой выплачиваются ежемесячно (проценты сложные).

Решение: обозначим через j номинальную ставку с начислением процентов m раз в год, через j1 номинальную ставку с начислением процентов m1 раз в год.

Приравняем соответствующие множители наращения

, тогда .

В таком случае наша искомая ставка 0,19, или 19 %.

Варианты задания № 5

1. Требуется определить номинальную процентную ставку с начислением процентов по полугодиям, которая эквивалентна номинальной ставке 50 % с ежемесячным начислением процентов (проценты сложные).

2. Найдите эффективную процентную ставку, эквивалентную номинальной ставке 150 % при ежемесячном начислении процентов (проценты сложные).

3. Найдите наращенную на 150$ сумму, инвестированную на 3 месяца по номинальной ставке 20 % годовых (проценты сложные).

4. Для номинальной ставки 20 % с начислением процентов 2 раза в год найдите эквивалентную ставку, проценты по которой выплачиваются ежемесячно (проценты сложные).

5. Определить номинальную ставку процентов, которая обеспечивала бы годовую доходность в 26 %, если начисление процентов происходит ежемесячно (проценты сложные).

6. Найдите наращенную на 350$ сумму, инвестированную на 5 месяцев по номинальной ставке 25 % годовых (проценты сложные).

7. Определить номинальную ставку процентов, которая обеспечивала бы годовую доходность в 30 %, если начисление процентов происходит ежемесячно (проценты сложные).

8. Найдите наращенную на 450$ сумму, инвестированную на 5 месяцев по номинальной ставке 20 % годовых (проценты сложные).

9. Найдите эффективную процентную ставку, эквивалентную номинальной ставке 50 % при ежеквартальном начислении процентов (проценты сложные).

10. Требуется определить номинальную процентную ставку с начислением процентов по полугодиям, которая эквивалентна номинальной ставке 55 % с ежемесячным начислением процентов (проценты сложные).

11. Найдите эффективную процентную ставку, эквивалентную номинальной ставке 120 % при ежемесячном начислении процентов (проценты сложные).

12. Определить номинальную ставку процентов, которая обеспечивала бы годовую доходность в 40 %, если начисление процентов происходит ежеквартально (проценты сложные).

13. Требуется определить номинальную процентную ставку с начислением процентов по полугодиям, которая эквивалентна номинальной ставке 27 % с ежемесячным начислением процентов (проценты сложные).

14. Определить номинальную ставку процентов, которая обеспечивала бы годовую доходность в 21 %, если начисление процентов происходит ежеквартально (проценты сложные).

15. Для номинальной ставки 30 % с начислением процентов 4 раза в год найдите эквивалентную ставку, проценты по которой выплачиваются ежемесячно (проценты сложные).

16. Определить номинальную ставку процентов, которая обеспечивала бы годовую доходность в 40 %, если начисление процентов происходит ежемесячно (проценты сложные).

17. Найдите эффективную процентную ставку, эквивалентную номинальной ставке 50 % при ежемесячном начислении процентов (проценты сложные).

18. Найдите наращенную на 150$ сумму, инвестированную на 5 месяцев по номинальной ставке 36 % годовых (проценты сложные).

19. Найдите наращенную на 450$ сумму, инвестированную на 3 месяца по номинальной ставке 20 % годовых (проценты сложные).

20. Найдите наращенную на 350$ сумму, инвестированную на 4 месяца по номинальной ставке 19 % годовых (проценты сложные).

21. Определить номинальную ставку процентов, которая обеспечивала бы годовую доходность в 20 %, если начисление процентов происходит ежемесячно (проценты сложные).

22. Требуется определить номинальную процентную ставку с начислением процентов по полугодиям, которая эквивалентна номинальной ставке 67 % с ежемесячным начислением процентов (проценты сложные).

23. Определить номинальную ставку процентов, которая обеспечивала бы годовую доходность в 21 %, если начисление процентов происходит ежемесячно (проценты сложные).

24. Найдите эффективную процентную ставку, эквивалентную номинальной ставке 10 % при ежемесячном начислении процентов (проценты сложные).

25. Для номинальной ставки 30 % с начислением процентов 2 раза в год найдите эквивалентную ставку, проценты по которой выплачиваются ежемесячно (проценты сложные).

26. Требуется определить номинальную процентную ставку с начислением процентов по полугодиям, которая эквивалентна номинальной ставке 54 % с ежемесячным начислением процентов (проценты сложные).

27. Определить номинальную ставку процентов, которая обеспечивала бы годовую доходность в 21 %, если начисление процентов происходит ежемесячно (проценты сложные).

28. Требуется определить номинальную процентную ставку с начислением процентов по полугодиям, которая эквивалентна номинальной ставке 25 % с ежемесячным начислением процентов (проценты сложные).

29. Для номинальной ставки 20 % с начислением процентов 4 раза в год найдите эквивалентную ставку, проценты по которой выплачиваются ежемесячно (проценты сложные).

30. Найдите наращенную на 150$ сумму, инвестированную на 7 месяцев по номинальной ставке 20 % годовых (проценты сложные).

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)

Источник

Калькулятор доходности вкладов

Онлайн калькулятор вкладов поможет вам быстро рассчитать проценты по любому вкладу, в том числе с капитализацией, с пополнениями и с учетом налогов, а также покажет график начисления процентов. Если вы планируете открыть вклад, то калькулятор поможет вам заранее рассчитать потенциальную доходность.

Капитализация процентов

При обычном вкладе начисленные проценты банк выплачивает вкладчику ежемесячно (либо с другой периодичностью, оговоренной условиями договора). Это называется «простые проценты». Вклад с капитализацией (или «сложные проценты») — это условие, при котором начисленные проценты не выплачиваются, а прибавляются к сумме вклада, таким образом увеличивая её. Общий доход от вклада в этом случае будет выше.

С помощью депозитного калькулятора вы можете сравнить результаты расчёта двух одинаковых вкладов (с капитализацией и без) и увидеть разницу.

Эффективная процентная ставка по вкладу

Эта характеристика актуальна только для вкладов с капитализацией процентов. В связи с тем, что проценты не выплачиваются а идут на увеличение суммы вклада, очевидно, что если ежемесячно возрастает сумма вклада, то и вновь начисленные на эту сумму проценты также будут выше, как и конечный доход.

Если рассчитать, сколько процентов было начислено к начальной сумме к концу срока вклада, эта величина и будет являться эффективной процентной ставкой.

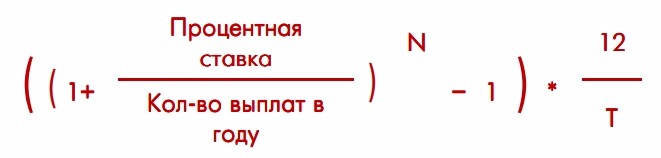
Формула расчета эффективной ставки:

где
N — количество выплат процентов в течение срока вклада,
T — срок размещения вклада в месяцах.

Эта формула не универсальна. Она подходит только для вкладов с капитализацией 1 раз в месяц, период которых содержит целое количество месяцев. Для других вкладов (например вклад на 100 дней) эта формула работать не будет.

Однако есть и универсальная формула для рассчета эффективной ставки. Минус этой формулы в том, что получить результат можно только после рассчета процентов по вкладу.

Эта формула подходит для всех вкладов, с любыми сроками и любой периодичностью капитализации. Она просто считает отношение полученного дохода к начальной сумме вклада, приводя эту величину к годовым процентам. Лишь небольшая погрешность может присутствовать здесь, если период вклада или его часть выпала на високосный год.

Именно этот метод используется для рассчета эффективной ставки в представленном здесь депозитном калькуляторе.

Налог на доход по вкладам

Как было до 2021 года

Налог начислялся в случаях, если ставка по вкладу превышала ключевую на 5 и более процентов. Размер налога был 35% и 30% для резидентов и нерезидентов соответственно. Начислялся он не на весь доход во вкладу, а только на разницу между доходом, вычисленным по пороговой ставке (ключевая ставка + 5%) и реально полученным доходом.

Как стало с 2021 года

• Налоговая ставка теперь 13% для всех.
• Введена необлагаемая сумма дохода. Все, что выше — облагается налогом. Количество вкладов не имеет значения, считается общая сумма на всех вкладах.
• Необлагаемый доход рассчитывается следующим образом:

В качестве примера возьмем 2021 год.

1. У Васи есть 2 вклада в разных банках. В первом банке 500 000 руб. под 5%, во втором банке 800 000 руб под 4%.
2. Ключевая ставка ЦБ на 1 января 2021 года была 4.25%.
3. Сумма необлагаемого дохода едина для всех вкладов и составляет 1 000 000 × 4.25% = 42 500 руб. С этой суммы налог платить не нужно.
4. Доход по вкладам васи за год составит: в первом банке — 25 000 руб., во втором — 32 000 руб. Всего — 57 000 руб.
5. Разница между фактическим и необлагаемым доходом составит 57 000 — 42 500 = 14 500 руб. Это тот доход, с которого необходимо заплатить НДФЛ.
6. Размер НДФЛ = 14 500 × 13% = 1 885 руб.

Наш депозитный калькулятор рассчитывает вклады с учетом налогов.

Источник

Определить номинальную процентную ставку через годовую доходность

Пусть годовая ставка сложных процентов равна j , а число периодов начисления в году m . Тогда каждый раз проценты начисляют по ставке j / m . Ставка j называется номинальной. Начисление процентов по номинальной ставке производится по формуле:

(1)

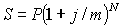
где N – общее число периодов начисления.

Если срок ссуды измеряется дробным числом периодов начисления, то при т разовом начислении процентов в году наращенную сумму можно рассчитывать несколькими способами, приводящими к различным результатам.

В банк вложены деньги в сумме 5 тыс. р. на два года с полугодовым начислением сложных процентов по ставке 20% годовых. Определить наращенную сумму и сравнить ее со случаем, если проценты начисляются ежеквартально.

Определим наращенную сумму при полугодовом начислении процентов по формуле (1):

= 5 × (1 + 0,2/2) 4 = 7,3205 тыс. р.

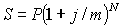
Если начисление будет производиться ежеквартально, то сумма к концу двух лет составит:

S = 5 × (1 + 0,2/4) 8 = 7,387 тыс. р.

Наращенная сумма при полугодовом начислении процентов к концу двух лет составит 7,3205 тыс. р., а при ежеквартальном – 7,387 тыс. р.

Кроме того, можно сделать следующие выводы:

— чем чаще в течении года происходит начисление по сложным процентам, тем больше наращенная сумма;

— при начислении сложных процентов 12% годовых неэквивалентно 1% в месяц;

— для простых процентов эти выводы недействительны. Одно из характерных свойств наращения по простым процентам заключается в том, что наращенная сумма не зависит от частоты начисления простых процентов. Например, наращение простыми процентами ежегодно по ставке 12% годовых дает тот же результат, что и ежемесячное наращение в течение года по ставке 1% в месяц.

— при наращении по сложным процентам ежемесячное начисление приносит больший результат, чем ежегодное один раз.

Размер ссуды 500 тыс. р., она предоставлена на 28 месяцев. Номинальная ставка равна 20% сложных годовых. Начисление процентов ежеквартальное. Вычислить наращенную сумму в трех ситуациях:

— когда на дробную часть начисляются сложные проценты,

— когда на дробную часть начис­ляются простые проценты,

— когда дробная часть не учитывается.

Результа­ты расчетов сравнить.

Начисление процентов ежеквартальное. Всего имеется 28/3 кварталов.

Определим наращенную сумму, когда на дробную часть начисляются сложные проценты:

S = 20 (1 + 0,6/4) 28/3 = 73,713 тыс. р.

Вычислим наращенную сумму, когда на целую часть года начисляются сложные проценты, а на дробную часть начис­ляются простые проценты:

S = 20 (1 + 0,6/4) 9 (1 + 0,6/4 × 1/3) = 73,875 тыс. р.

Найдем наращенную сумму, когда дробная часть года не учитывается:

S = 20 ( l + 0,6/4) 9 = 70,358 тыс. р.

Наращенные суммы в трех рассмотренных случаях составляют 73, 713 тыс. р., 73,875 тыс. р., 70,358 тыс. р.

Из полученных результатов расчета следует, что наибольшего значения наращенная сумма достигает во втором случае, т.е. при начислении на дробную часть простых процентов, наименьшее значение – в третьем случае, когда наращение дробной части года не учитывается.

Источник

Как рассчитать проценты по вкладу

Формулы и примеры расчета с капитализацией, пополнением, частичным снятием

Банки предлагают разные вклады со своими названиями и условиями. И предложение с самой высокой процентной ставкой может оказаться не самым выгодным — нужно смотреть условия и рассчитывать реальную доходность. Как понять, что выгоднее: открыть депозит с процентными выплатами в конце срока, но под 6,1% годовых или с ежемесячной капитализацией, но под 6% годовых? Разбираемся.

Годовые проценты

Для сравнения условий вкладов используется годовая доходность. Можно вычислить, например, квартальную ставку, но удобнее сравнивать именно годовую.

Банки в своих предложениях указывают номинальную ставку годовых, которая не учитывает капитализацию, если она есть. В этом случае полезно посчитать эффективную процентную ставку.

Эффективная процентная ставка позволяет сравнивать вклады с разными условиями: например, по одному вкладу проценты начисляются раз в месяц и капитализируются, а по другому выплачиваются в конце срока. Эффективная ставка позволяет привести эти два вклада к общему знаменателю и понять, какой из них выгоднее.

Вычисление эффективной процентной ставки

Для вычисления эффективной ставки по вкладам используется формула:

• С — номинальная ставка (в процентных пунктах);
• П — количество периодов капитализации в год;
• Д — длительность (срок) депозита в годах.

Период капитализации — это интервал времени, в конце которого начисляются проценты. У банковского вклада без капитализации проценты начисляются один раз за год в конце срока — значит, П = 1. При ежемесячной капитализации П = 12, при ежеквартальной П = 4, а если проценты начисляются каждый день, П = 365.

Зная эффективную процентную ставку, можно сравнивать банковские продукты с разными схемами начисления процентов. Вот некоторые банковские опции по депозитам.

Вклады с капитализацией

Если банк капитализирует проценты по вкладу — начисляет и добавляет их к сумме депозита, — такой вариант будет выгоднее при прочих равных условиях. Периодичность капитализации может быть разная, обычно — раз в месяц. Периодичность указана в договоре: чем чаще — тем быстрее будет увеличиваться сумма на депозите и тем больше банк начислит процентов за следующий период.

Например, вы открыли депозит на 100 000 Р под 6% годовых на 1 год с ежемесячной капитализацией. Каждый месяц банк будет начислять проценты и добавлять их к сумме вклада.

Упрощенный расчет будет выглядеть так:

С каждым месяцем сумма, на которую начисляются проценты, будет расти. Соответственно, и процентов каждый месяц будет начисляться больше.

Для вычисления эффективной процентной ставки подставим в формулу параметры нашего депозита. Базовая ставка 6% — значит, С = 6. Проценты капитализируются каждый месяц (то есть 12 раз в год) — П = 12, вклад на год — Д = 1.

С ежемесячной капитализацией номинальная ставка 6% превратилась в эффективную годовую процентную ставку около 6,167%.

Это значит, что наш депозит с ежемесячной капитализацией под 6% равнозначен вкладу без капитализации и с выплатой в конце срока под 6,167%. То есть депозит под 6% и с капитализацией будет выгоднее, чем под 6,1%, но без капитализации.

Если открыть вклад с теми же условиями, но на 2 года, эффективная ставка будет выше:

Вклады с пополнением

Если по условиям договора вклад можно пополнять — вносить дополнительные средства, — с момента внесения процент начисляется на общую сумму.

Пример: вы открыли счет на 100 000 Р под 8% годовых на 1 год с возможностью пополнения, а через полгода внесли еще 50 000 Р . При годовой ставке 8% за полгода банк начислит 4% от суммы депозита. Рассчитаем процентные начисления за каждые полгода отдельно:

Без учета капитализации сумма процентных начислений составит 10 000 Р . Вкладчик в этом случае получает фиксированный процент от вложенных денег, поэтому эффективная ставка здесь не меняется — 8% годовых.

Если вклад с капитализацией, для вычисления эффективной процентной ставки можно отдельно рассчитать периоды до и после пополнения — как будто это два разных депозита. Эффективная ставка у вкладов будет другой из-за изменения длительности. Для каждого вычисляем сумму процентов, складываем, делим на среднюю сумму вложений без учета начисленных процентов и на общую длительность.

• СО — это средний остаток по счету в течение всего срока, как если бы вы клали деньги на беспроцентный депозит;
• Д — общая длительность вклада в годах.

Это и есть смысл эффективной ставки: она показывает, под какой процент нужно вложить средний остаток по счету, чтобы получить те же проценты за тот же срок.

Вклады с частичным снятием

Иногда по условиям договора банк разрешает снимать со счета часть средств, которые лежат на депозите. При этом проценты с момента открытия депозита до момента снятия не теряются.

Пример: вы открыли депозит на 100 000 Р под 8% годовых на 1 год с возможностью частичного снятия, а через полгода сняли 50 000 Р . При годовой ставке 8% за полгода банк начислит 4% от суммы вклада. Рассчитаем проценты за каждые полгода отдельно.

Без капитализации сумма процентов составит 6000 Р . Эффективная процентная ставка без ежемесячной капитализации — те же 8%.

Расчет эффективной ставки с капитализацией можно произвести аналогично вкладу с пополнением.

Источник