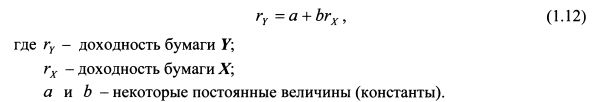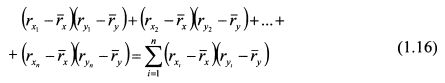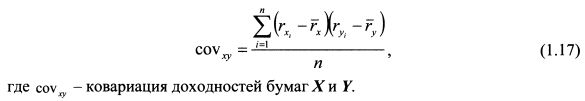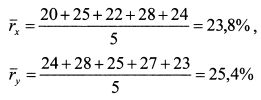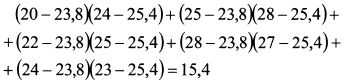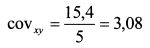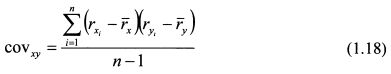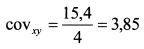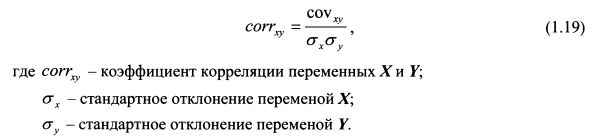1.2.3. Показатели тесноты связи между доходностями ценных бумаг
Риск ценной бумаги измеряется такими показателями как дисперсия или стандартное отклонение. Поэтому ожидаемый риск портфеля представляет собой сочетание стандартных отклонений (дисперсий) входящих в него бумаг. Однако в отличие от ожидаемой доходности портфеля его риск не является обязательно средневзвешенной величиной стандартных отклонений (дисперсий) доходностей бумаг. Дело в том, что разные активы могут не одинаково реагировать на изменение конъюнктуры рынка. В результате стандартные отклонения (дисперсии) доходности различных бумаг в ряде случаев будут погашать друг друга, что приведет к снижению риска портфеля. Риск портфеля зависит от того, в каком направлении изменяются доходности входящих в него активов при изменении конъюнктуры рынка и в какой степени. Поэтому при формировании портфеля ценных бумаг инвестору необходимо знать, каким образом будет изменяться доходность одного актива при изменении доходности другого актива.
Между доходностями ценных бумаг может наблюдаться функциональная зависимость. Это означает, что существует строгое правило, которое связывает значения их доходностей. Наиболее простой является линейная зависимость. Ее можно представить в следующем виде:
При линейной зависимости одному значению доходности бумаги X соответствует строго одно значение доходности бумаги F. Уравнение (1.12) представляет положительную зависимость между Хи Y. Об этом говорит знак
плюс перед коэффициентом b. Графически данная зависимость представлена на рис. 1.4.
Как видно из графика на рис. 1.4, при росте доходности бумаги X доходность бумаги Y также возрастает, и наоборот. Константа а представляет собой значение точки, в которой график функции пересекает ось OY (ось ординат). Константа b показывает угловой коэффициент наклона графика к оси ОХ (оси абсцисс) и равна тангенсу данного угла.
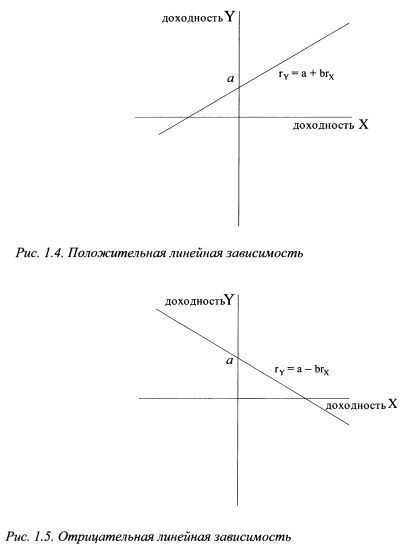
Если зависимость задана уравнением:
(перед коэффициентом b стоит знак минус), это означает, что она отрицательная. График функции (1.13) представлен на рис. 1.5. Как из него следует, при росте доходности бумаги X доходность бумаги Y падает, и наоборот.
На финансовом рынке зависимость между доходностями ценных бумаг часто бывает не функциональной, т. е. не жесткой. В этом случае одному значению доходности одной бумаги могут соответствовать разные значения доходности другой бумаги. Таким образом, не наблюдается строгого закона, который бы связывал значения их доходностей. Зависимость подобного рода называют стохастической или вероятностной, или статистической. Это означает, что при изменении доходности одной бумаги можно говорить лишь о том, какие значения доходности может принять другая бумага и с какой вероятностью. Такое положение вещей объясняется существованием большого количества факторов, влияющих на доходности конкретных активов и тем, что все их сложно учесть.
При формировании портфеля степень взаимосвязи между доходностями двух ценных бумаг можно определить с помощью таких показателей как ковариация и коэффициент корреляции.
Ковариация говорит о степени зависимости двух случайных величин. Она может принимать положительные, отрицательные значения и равняться нулю. Если ковариация положительна, это говорит о том, что при изменении значения одной переменной другая имеет тенденцию изменяться в том же направлении. Так, при положительной ковариации доходностей двух бумаг с ростом доходности первой бумаги доходность второй также будет расти. При падении доходности первой бумаги доходность второй также будет снижаться.
При отрицательной ковариации переменные имеют тенденцию изменяться в противоположных направлениях. В таком случае рост доходности первой бумаги будет сопровождаться падением доходности второй бумаги, и наоборот. Чем больше значение ковариации, тем сильнее зависимость между переменными. Если ковариация равна нулю, никакой зависимости между переменными не наблюдается.
Приведем общий принцип расчета ковариации. Пусть имеются статистические данные по доходности бумаг Х и F за п лет. Доходность бумаги X за первый год равна rх1, второй — rх2. п-й — rхn. Соответственно доходность бумаги Y за первый год составила ry1, второй – ry2. п-й — ryn. Необходимо рассчитать ковариацию доходностей бумаг. Разобьем расчеты на несколько шагов. ШАГ 1. Определяем среднюю доходность бумаг Хи F за п лет. Это просто средняя арифметическая доходности по каждой бумаге. Соответственно:
ШАГ 2. Находим отклонения фактической доходности бумаг для каждого периода от средней доходности. Для бумаги X:
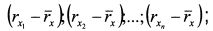
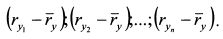
ШАГ 4. Делим полученную сумму на количество наблюдений. Это и будет ковариация доходностей бумаг:
Доходность бумаги X за пять лет составила соответственно 20%, 25%, 22%, 28%, 24%. Доходность бумаги Y: 24%, 28%, 25%, 27%, 23%. Определить ковариацию доходностей бумаг.
Определяем среднюю доходность бумаг по формулам (1.14) и (1.15):
В соответствии с формулой (1.16) находим отклонения доходностей бумаг для каждого периода, перемножаем их и суммируем:
Определяем ковариацию по формуле (1.17):
При расчете ковариации используется только выборка из генеральных совокупностей доходностей ценных бумаг, поскольку невозможно учесть все их значения. Поэтому по формуле (1.17) получают ковариацию, которая называется выборочной. В этом случае оценка ковариации будет иметь отрицательное смещение, так как отклонения считаются не от истинного среднего значения переменных, а от выборочных средних. Выборочные средние непосредственно находятся в центре выборки и поэтому отклонения от них в среднем меньше, чем от действительных средних значений переменных. Оценка ковариации будет несмещенной, если в формуле (1.17) в знаменателе величину п заменить на (n-1):
Для нашего примера несмещенная оценка ковариации составляет:
Следует, однако, отметить, что для больших выборок данная корректировка знаменателя уже не играет существенного значения.
Ковариация имеет некоторые недостатки, которые приводят к неудобству ее использования для получения объективной картины тесноты связи между переменными. Так ковариация имеет размерность равную произведению размерности двух случайных величин. Поэтому значение ковариации зависит от единиц их измерения. Если бы в нашем примере мы взяли доходности не в процентах, а в десятичных значениях, т.е. не 20%, а 0,2, не 24%, а 0,24 и т.д., то получили бы значение ковариации равным 0,000385.
Далее, как следует из формул (1.17) и (1.18), ковариация характеризует не только зависимость переменных, но и их рассеяние вокруг средних значений. В результате, если одна из переменных мало отклоняется от своего среднего значения, то величина ковариации будет небольшой, какой бы тесной не была зависимость переменных Хи Y. Поэтому ковариация не позволяет получить наглядную картину степени взаимосвязи между переменными. В результате от ковариации переходят к коэффициенту корреляции. Он определяется по формуле:
Коэффициент корреляции характеризует степень тесноты линейной зависимости двух переменных и является безразмерной величиной. Тенденция к линейной зависимости двух переменных может иметь более или менее выраженный характер. Поэтому значения коэффициента изменяются в диапазоне от -1 до +1. Если коэффициент равен +1, между доходностями двух бумаг существует положительная функциональная зависимость, соответствующая формуле (1.12). График ее представлен на рис. 1.4. В таком случае одному значению доходности бумаги X строго соответствует одно значение доходности бумаги F. Таким образом, все возможные значения доходностей X и Y располагаются на прямой восходящей линии. Знак плюс указывает на то, что доходности изменяются в одном направлении: или обе растут, или обе падают.
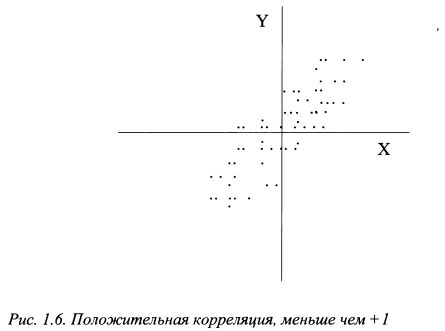
Если коэффициент корреляции положительный, но меньше чем +1, между доходностями двух бумаг также существует зависимость, но менее строгая. На рис. 1.6 представлен случай положительной корреляции между доходностями бумаг Х и F, но меньшей чем +1. Конкретные значения доходностей бумаг даны на графике отдельными точками и представляют собой некоторое рассеяние. Несмотря на отсутствие строгой зависимости между переменными, наглядно видно, что в целом выполняется закономерность: большему значению X соответствует большее значение Y. Поскольку корреляция меньше чем +1, то в отдельных случаях при росте доходности бумаги X доходность Y может и падать. Таким образом, положительная корреляция означает, что при возрастании одной из переменных другая имеет тенденцию в среднем возрастать.
Важно: актуальное предложение по поводу компенсации до 100% комиссии, взимаемой Вашим брокером.
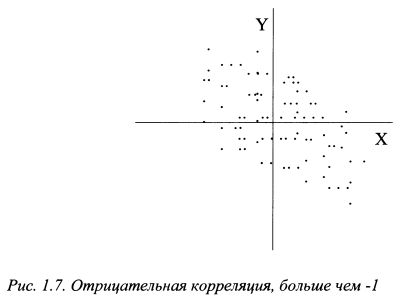
Если коэффициент корреляции равен -1, между доходностями бумаг существует отрицательная функциональная зависимость, соответствующая формуле (1.13). Ее график представлен на рис. 1.5. В этом случае при росте доходности бумаги X доходность Y падает, и наоборот. Все возможные значения X и Y располагаются на нисходящей прямой линии. Случай отрицательной корреляции, но большей чем минус один, представлен на рис. 1.7. По форме рассеяния значений X и Y можно сделать вывод о том, что в целом между переменными наблюдается закономерность: большему значению X соответствует меньшее значение F, и наоборот. Однако, поскольку зависимость не строгая, в динамике значений переменных могут иногда наблюдаться движения и в одном направлении. Таким образом, при отрицательной корреляции при возрастании доходности одной бумаги доходность другой имеет тенденцию в среднем убывать.
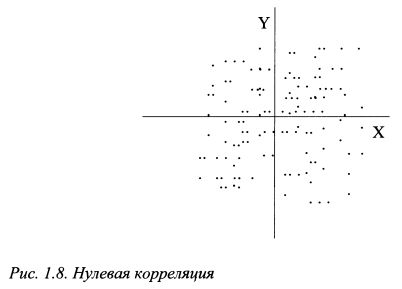
При коэффициенте корреляции равном нулю никакой зависимости между переменными нет. Картина значений переменных X и Y будет представлять некоторое рассеяние, по которому нельзя обнаружить какое-либо подобие нисходящей или восходящей закономерности. Такая ситуация представлена на рис. 1.8.
Вернемся к примеру с доходностями бумаг X и Y и рассчитаем для них коэффициент корреляции. Полученная ковариация равнялась 3,85. Стандартные отклонения доходностей бумаг X и Y соответственно составляют:
Источник
Ковариация | Covariance
Математически ковариация (англ. Covariance) представляет собой меру линейной зависимости двух случайных величин. В портфельной теории этот показатель используется для определения зависимости между доходностью определенной ценной бумаги и доходностью портфеля ценных бумаг. Чтобы рассчитать ковариацию доходности необходимо воспользоваться следующей формулой:
где ki – доходность ценной бумаги в i-ом периоде;

pi – доходность портфеля в i-ом периоде;

n – количество наблюдений.
Следует отметить, что в знаменатель формулы подставляется (n-1), если ковариация рассчитывается на основании выборки из генеральной совокупности наблюдений. Если в расчетах учитывается вся генеральная совокупность, то в знаменатель подставляется n.
Пример. В таблице представлена динамика доходность акций Компании А и Компании Б, а также динамика доходности портфеля ценных бумаг.
Чтобы воспользоваться вышеприведенной формулой для расчета ковариации доходности каждой из акций с портфелем необходимо рассчитать среднюю доходность, которая составит:
- для акций Компании А 4,986%;
- для акций Компании Б 5,031%;
- для портфеля 3,201%.
Таким образом, ковариация акций Компании А с портфелем составит -0,313, а акций Компании Б 0,242.
Cov (kA, kp) = ((5,93-4,986)(2,27-3,201) + (5,85-4,986)(2,39-3,201) + (5,21-4,986)(3,47-3,201) + (5,37-4,986)(3,21-3,201) + (4,99-4,986)(2,95-3,201) + (4,87-4,986)(2,97-3,201) + (4,70-4,986)(3,32-3,201) + (4,75-4,986)(3,65-3,201) + (4,33-4,986)(3,97-3,201) + (3,86-4,986)(3,81-3,201))/(10-1) = -0,313
Cov (kБ, kp) = ((4,25-5,031)(2,27-3,201) + (4,47-5,031)(2,39-3,201) + (4,68-5,031)(3,47-3,201) + (4,71-5,031)(3,21-3,201) + (4,77-5,031)(2,95-3,201) + (5,25-5,031)(2,97-3,201) + (5,45-5,031)(3,32-3,201) + (5,33-5,031)(3,65-3,201) + (5,55-5,031)(3,97-3,201) + (5,85-5,031)(3,81-3,201))/(10-1) = 0,242
Аналогичные расчеты можно произвести в Microsoft Excel при помощи функции «КОВАРИАЦИЯ.В» для выборки из генеральной совокупности или функции «КОВАРИАЦИЯ.Г» для всей генеральной совокупности.
Интерпретация ковариации
Значение коэффициента ковариации может быть как отрицательным, так и положительным. Его отрицательное значение говорит о том, что доходность ценной бумаги и доходность портфеля демонстрируют разнонаправленное движение. Другими словами, если доходность ценной бумаги будет расти, то доходность портфеля будет падать, и наоборот. Положительное значение свидетельствует о том, что доходность ценной бумаги и портфеля изменяются в одном направлении.
Низкое значение (близкое к 0) коэффициента ковариации наблюдается в том случае, когда колебания доходности ценной бумаги и доходности портфеля носят случайный характер.
Источник