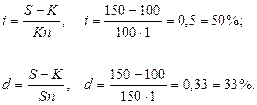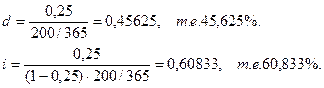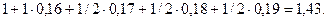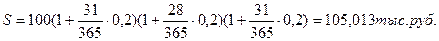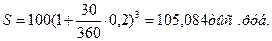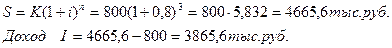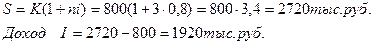- Определить годовую доходность для кредитора
- (3)
- Формулы доходности финансовых операций
- Цифры, числа и проценты — как правильно считать прибыль и годовую доходность | Несколько простых способов с интересными примерами
- Складываем годовые доходности
- Прибыль + убытки — как сложить?
- Методы 72
- Метод 114
- Среднегодовая прибыль за несколько лет
Определить годовую доходность для кредитора
Определение процентной ставки
Уровень процентной ставки является мерой доходности операции, критерием сопоставления альтернатив и выбора наиболее выгодных условий. Из формул
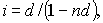
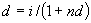
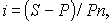
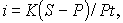
 (3)
(3)
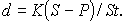
Следует отметить, что срок п, t в этих формулах имеет разный смысл: в (1) и (2) это весь срок операции, а в (3) и (4) — оставшийся срок до погашения.
Определить доходность операции для кредитора, если им предоставлена ссуда в размере 200 тыс. р. на 60 дней и контракт предусматривает сумму погашения долга 210 тыс. р. Доходность выразить в виде простой ставки процентов i и учетной ставки d. Временную базу принять равной К = 360 дней.
По формуле (2.) определим доходность операции в виде простой ставки процентов:
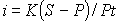
По формуле (4) определим доходность операции в виде простой учетной ставки:
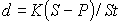
Доходность операции, выраженная в виде простой ставки составляет 30%, а в виде простой учетной ставки – 28,6%.
Источник
Формулы доходности финансовых операций



Если в формулах наращения по процентной и учетной ставке принять срок n = 1 году, то получим, что
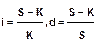
Если n
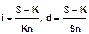
Эти формулы принято называть формулами доходности или эффективности по простой ставке процентов и учетной ставке соответственно.
Предприятие получило кредит на 1 год в размере 100 млн. с условием возврата 150 млн.
Найти доходность операции для кредитора в виде процентной и дисконтной (учетной) ставок.
К = 100 млн., S = 150 млн., n = 1 год. I = ?, d = ?
Решение:
Дисконтная ставка всегда меньше процентной, ибо она учитывает время более жестко.
Иногда размер дисконта в контрактах фиксируется за весь срок ссуды в виде доли (или процента) от суммы погасительного платежа. Таким образом, уровень процентной ставки задается в неявном виде. Выведем формулы, с помощью которых можно вычислить значения этих ставок.
Пусть S- размер погасительного платежа (сумма ссуды к концу срока),
dn – доля этого платежа, определяющая величину дисконта за весь срок ссуды.
К = S(1 – dn) – реально выдаваемая ссуда в момент заключения договора.
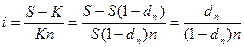 |
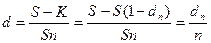 |
Задача 7.
Кредитор и заемщик договорились, что из суммы кредита, выданного на 200 дней, сразу удерживается дисконт в размере 25% указанной суммы. Требуется определить цену кредита в виде простой годовой учетной ставки d и годовой простой ставки i. Год полагать равным 365 дней.
Простые переменные ставки
В кредитных соглашениях иногда предусматриваются изменяющиеся во времени процентные ставки.
Если i1, i2,… ik – последовательные во времени простые ставки,
а n1, n2,… nk – периоды, в течение которых применяются соответствующие ставки, тогда наращенная сумма определяется следующим образом:
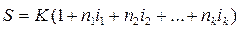 |
Контракт предусматривает следующий порядок начисления процентов: первый год – ставка 16%, в каждый последующем полугодии ставка повышается на 1%. Определить множитель наращения за 2,5 года.
Общий срок начисления процентов 1+1/2+1/2+1/2=2,5 года.
Множитель наращения =
Иначе, за 2,5 года начальный капитал увеличился в 1,43 раза.
Реинвестирование
В практике при реинвестировании средств в краткосрочные депозиты иногда прибегают к неоднократному последовательному повторению наращения по простым процентам в пределах заданного общего срока, т.е. к реинвестированию средств, полученных на каждом этапе наращения. (Напоминает наращение по сложным процентам, но только напоминает!)
В этом случае наращенная сумма для всего срока составит:
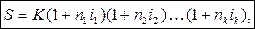
Если периоды начисления и ставки не изменяются во времени, то формула реинвестирования примет вид:
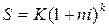
Задача 9.
Сумму в 100 тысяч рублей положили 1 января на месячный депозит под 20% годовых. Каковой будет наращенная сумма, если операция повторяется 3 раза? Расчет сделать по точным и банковским процентам.
По условию задачи депозит в 100 тысяч рублей реинвестируется трижды по простым процентам.
По точным процентам:
(Помните, что в январе 31 день, в феврале – 28 дней, в марте – 31 день!)
По банковским процентам при условии, что в каждом месяце по 30 дней:
Модуль 2. Сложные проценты
Наращение по сложным процентам
В среднесрочных и долгосрочных операциях, если проценты не выплачиваются сразу после их начисления, а присоединяются к сумме долга, то для наращения используются сложные проценты.
Сложные проценты отличаются от простых процентов базой начисления. Если в простых процентах она остается постоянной на весь срок начисления, то в сложных при каждом начислении процентные деньги присоединяются к первоначальной базе. Говорят, идет капитализация процентов.
Формула наращения по сложным процентам, если проценты начисляются один раз в году, имеет вид

(1) 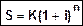
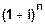
Задача 1.
Сумма, равная 800 тыс. руб., инвестируется на 3 года под 80% годовых. Найти наращенную сумму и сумму процентов за этот срок, используя простые и сложные проценты.
2. Простые проценты:
За 3 года 800 тыс. руб. увеличились в 5,832 раза по сложным процентам и только в 3,4 раза по простым процентам.
Задача 2.
Сумма, равная 800 тыс. руб., инвестируется на 3 месяца под 80% годовых. Найти наращенную сумму и сумму процентов за этот срок, используя простые и сложные проценты.
Источник
Цифры, числа и проценты — как правильно считать прибыль и годовую доходность | Несколько простых способов с интересными примерами
Проходили в школу простые и сложные проценты? Ну как вам? Скукотища. Какие-то цифры, числа. Математические действия: умножение, деление, вычитание и сложение. Но все меняется, когда речь идет о деньгах. Собственных деньгах. Потенциале их роста от инвестиций. Сразу происходит смена настроения абсолютно на противоположное. От просто скучно до интересно.
И самыми любимыми становятся сложение и умножение. Складывать (суммировать) капитал и приумножать (зарабатывать) прибыль.
Расскажу про пару способов и приемов, как можно достаточно просто и быстро оценивать и считать результаты вложений (будущие и реальные). И главное, правильно.
Есть еще люди «в наших селеньях», кто не знает (или просто забыл) как все это делается.
Нам нужен калькулятор и один палец (не показывать, а нажимать на кнопки). В некоторых случаях просто мозги.
Складываем годовые доходности
Вы получили в первый год прибыль в 10%, во второй снова 10%. А на третий год? . опять десять.
Внимание вопрос. Сколько вы заработали за 3 года?
Быстрый ответ — 30% прибыли.
Мы посчитали 30% по правилам простых процентов. Просто сложив их вместе.
Если срок короткий и (или) доходность небольшая (не 20-30 и тем более не 50-100%), то результат будет близок к истине. Но как вы поняли, неправильный.
Представьте, что в течение 7 лет вы получаете по 10% годовых на вложенный капитал. Пусть будет на 100 тысяч.
Сколько мы заработаем за этот срок?
Снова быстрый ответ: 70% прибыли или 70 тысяч.
На самом деле — 95 тысяч рублей. Вы только что потеряли (недосчитали) 25 000.
Доходности нужно не складывать, а умножать между собой.
10% со 100 рублей, дадут 10. В совокупности будет 110.
Во второй год 10% берем со 110 — 11. Получаем в итоге — 121 рубль.
Третий год — принесет нам 12,1. Итого — 133,1 рубль.
Как это все подсчитать?
Проценты преобразуем по формуле: 1+ (доходность за год/100%). И перемножаем.
Соответственно 20% — это будет 1.2; 30% -1.3; 45% — 1.45.
В нашем случае: 1,1 х 1,1 х 1,1 и так далее. семь раз.
Прибыль + убытки — как сложить?
Как сложить между собой прибыльные и убыточные периоды?
Простой вопрос. В первый год получили прибыль +10% . За второй убыток -10% . Сколько денег будет в итоге?
Вроде бы плюс на минус дает ноль. Десять туда, 10% обратно.
Мы в той же точке отсчета.
На самом деле мы потеряли 1% (можете проверить на калькуляторе).
Причем последовательность не важна. Получена сначала прибыль, потом убыток. Или наоборот. Результат будет один.
Как быстро подсчитать?
- 10 процентов прибыли — 1,1;
- 10% убытка — 0,9.
Формула: 1- (убыток за период/100).
Перемножаем числа между собой и получаем результат.
В нашем случае: 1.1 Х 0.9 = 0,99. Или 99% от первоначального капитала.
Методы 72
Метод семидесяти двух позволяет быстро узнать, через сколько лет ваши вложения удвоятся.
Для этого нужно число 72 разделить на ожидаемую годовую доходность.
Например, при ежегодной прибыли в 7% — вы удвоите капитал примерно через 10 лет.
Увеличиваем доходность до 14,4% — и каждые 5 лет получаем прибыль 100%.
Через 10 лет у вас будет в четыре раза больше денег, через 15 — в 8 раз, через 20 — в 16.
Ну а «потерпев» 30 лет — вы увеличите свой капитал в 64 раза.
Метод 72 не блещет математической точностью. Всегда есть небольшая погрешность. Но на лету быстро посчитать и получить приблизительный результат — самое оно.
Кстати формула работает и в обратном направлении.
Ежегодный убыток в 6%, примерно через 12 лет ополовинит ваш капитал.
Интересно это использовать при инфляции. Насколько уменьшается покупательная способность денег.
Средняя инфляции в РФ за последние десять лет составила 7,43%.
Это значит, что рубль «усох» в 2 раза за 9,5 лет.
Метод 114
Все аналогично способу подсчета 72 (делим 114 на годовой доход). Но формула показывает утроение капитала за период. Тоже с небольшой погрешностью.
Пара примеров утроения капитала.
При доходности в год:
- 8% | (114 / 8) = 14,2 года
- 10% | (114 / 10) = 11,4 года
- 12% | (114 / 12) = 9,5 лет
- 14% | (114 / 14) = 8,1 год.
Среднегодовая прибыль за несколько лет
Как посчитать среднегодовую прибыль за различные периоды? А зачем?
Начнем с примера. Дальше поймете, нужна вам эта инфа или нет.
Два инвестора Вася и Петя начинаются мериться своими достоинствами доходностями. У кого больше. И кто круче.
Вася: Я раскачал свои 250 тысяч за 5 лет до 580 кусков. Заработал 330 000 рублей прибыли.
Петя: Мои скромные 40 тысяч я превратил в сотку всего за 6 лет. Прибыль 60 тысяч.
А кто из них действительно в большем плюсе от суммы вложенного капитала. У кого прибыль в процентах выше?
Вася за 5 лет получил 132% прибыли.
Петя заработал 150%, но за 6 лет.
Можно выделить среднегодовую доходность и увидеть, кто зарабатывал в год больше. Делим общий процент прибыли на количество лет.
Вроде бы Вася круче. У него больше. Хоть и ненамного.)))
Но мы немного неправильно вычленили годовую доходность.
Среднегодовая доходность = n√(Pn/P0)-1; где
- n — количество периодов (лет);
- P0 — начальное значение капитала;
- Pn — конечное размер
УУУУ. Какие-то корни. И даже не квадратные. И еще не все калькуляторы это поддерживают. Забудьте ее навсегда.
Мне больше нравится считать в электронных таблицах (Excel вам в помощь).
Есть такая формула.
=степень (Pn/P0; 1/n) — 1
Вносим 3 параметра — начальный, конечный капитал и срок вложений.
Получаем:
Рост за 6 лет у Пети с 40 до 100 тысяч соответствует среднегодовой доходности в 16,5%.
Вася, получивший сверху 330 тысяч за 5 лет зарабатывал в среднем по 18,3%.
Обратите внимание, как кардинально поменялись результаты по сравнению с простым делением общей прибыли на количество лет.
И наш «крутыш» Вася хоть и остается в лидерах, но среднегодовая прибыль уменьшилась почти в 1,5 раза..
Где еще можно применять такую формулу?
Для примера несколько вариантов использования.
Биржевые графики
Смотрим на какой нибудь биржевой график (акции, индекс, ETF). Нам нужно примерно оценить как он растет в среднем в год. На сколько процентов?
Например, за последние 5, 10, 20, 30 лет (да хоть сто лет).
Можно конечно поискать информацию в интернете. Есть различные статистические данные. Таблицы. Красивые цифры.
Но мы легкие пути не ищем. Рассчитаем все сами.
Нам нужна бутылка водки (хотя можно и без нее обойтись), начальная и конечная цена за требуемый период.
И электронная таблица. Особенно, если есть какой-то готовый шаблон — дело пары секунд (Спойлер: шаблон есть ниже). Вносим 3 числа и результат моментально перед глазами.
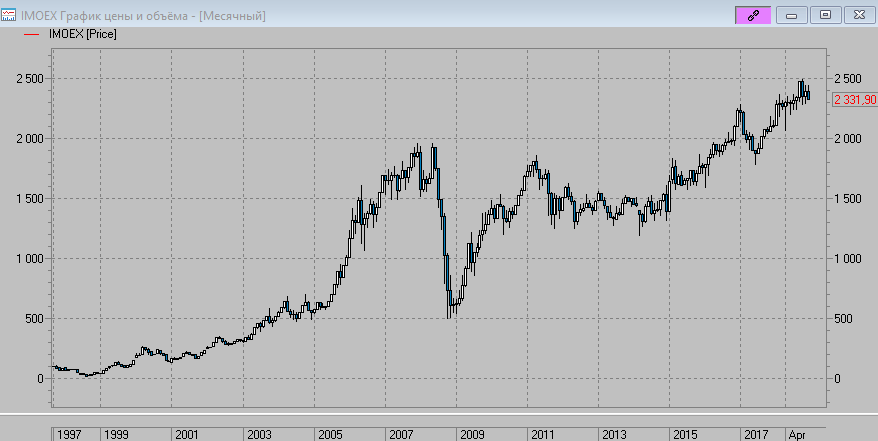
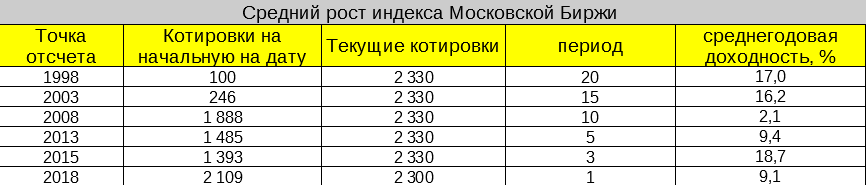
Для примера возьмем наш любимый и родной индекс Московской биржи. С момента его основание и по текущий момент.
Текущий (2018 год) еще правда не закончился (конец декабря). Но это не сильно критично.
В таблице видно на сколько процентов в среднем рос рынок в зависимости от точки входа.
Интересный момент с удорожанием продуктов.
Стоила лет десять назад булка хлеба 10 рублей. А сейчас ее цена 35 рубликов.
Молоко продавали за 20, а сейчас за 60 (данные я взял с потолка, просто для примера).
И так понятно, что грабеж среди бела дня. Но как его подсчитать?
Забиваем данные в таблицу и видим, что хлеб дорожал в среднем на 13,3% в год. А молоко всего на 11,6%.
Чего нам ждать в будущем: выравнивание пропорции цен? Хлеб стоит явно дороже, чем должен. Значит . скоро цены на него снизятся. ))))
А может на молочко еще подрастут (что более вероятно).
Дивиденды
Вернее темпы их роста. Интересная штука, скажу я вам.
Дивидендные аристократы (обычно компании из Америки) из года в год стараются повышать уровень выплат для своих акционеров. В России есть немного таких компаний, действующих подобных образом.
Вот статистика выплат дивидендов за последние несколько лет.
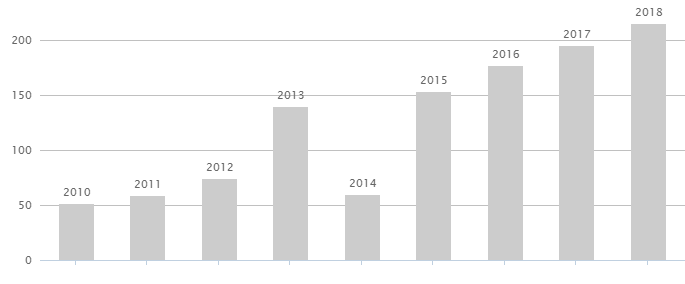
За восемь лет, размер дивидендов вырос со скромных 52 рубля на акцию в 2010, до 215 рублей в 2018 году. Ежу понятно, что это уже неплохо. Но . насколько неплохо?
С помощью формулы, можно определить среднегодовой темп прироста дивидендов.
Получаем 19,4% в год. Рост прибыли только за счет дивидендов. (Котировки на акции Лукойл тоже за это время выросли порядком). Обгоняющий инфляцию минимум в 2 раза.
Ради интереса рассчитал темпы роста дивов по другим голубым фишкам российского рынка: Газпром, Сбербанк и МТС.
Очень любопытная картина получилась.

По старой традиции для ленивых (или тех кто ценит свое время) прикладываю файл со всем, что здесь было написано, описано, рассчитано. Может кому и пригодится. При необходимости переделайте под себя.
Всем удачных (и правильно подсчитанных) положительных доходностей!
За обновлениями в этой и других статьях теперь можно следить на Telegram-канале: @vsedengy.
Источник
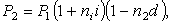
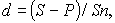 (3)
(3)