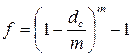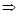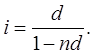Эквивалентность процентных ставок



При заключении финансовых контрактов каждый участник сделки стремится заключить контракт на наиболее выгодных для себя условиях. Условия контракта могут быть различными, и надо иметь возможность сравнивать контракты. При этом различные контракты могут предусматривать различные виды начисления процентов и для сравнения таких контрактов надо разработать способы приведении различных процентных ставок к одному виду. Напомним формулы для вычисления наращенной суммы S для всех видов процентных ставок:
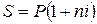
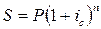
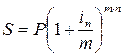
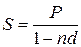
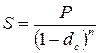
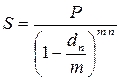
Во всех формулах есть число лет (n), оно может быть дробным.
Две процентные ставки называются эквивалентными, если применение их к одинаковым суммам в течение одинаковых промежутков времени дает одинаковые наращенные суммы.
Приравнивая правые части каких-либо двух из приведенных выше формул и выражая из этого равенства одну процентную ставку через другую, получаем условие эквивалентности соответствующих процентных ставок за n лет.
Пример решения задачи
Определите значение учетной ставки банка, эквивалентной ставке процентов, равной 40 % годовых.
Решение. Рассмотрим будущую стоимость этих сумм для одного года: 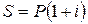
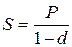
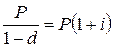
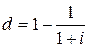
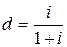
Таким образом, для заданной i = 40 %
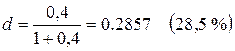
Для расчета эффективности финансовых операций используют сравнительную доходность, которая на основе допущения о равенстве финансовых результатов различных вариантов инвестиций приводит к понятию эквивалентных ставок простых или сложных процентов. Это позволяет получить инструмент корректного сравнения финансовых операций.
Эффективная ставка процентов измеряет относительный доход, который получают в целом за год от начисления процентов несколько раз в год:

Иначе говоря, эффективная ставка показывает, какая годовая ставка сложных процентов дает такой же финансовый результат, что и m-разовое начисление в год по ставке 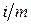
Под эффективной учетной ставкой понимают сложную годовую учетную ставку, эквивалентную номинальной при заданном значении m и вычисляют по формуле:
Пример решения задачи.Банк начисляет проценты на вклад исходя из номинальной ставки 12 % годовых. Определить эффективную (годовую) ставку при ежедневной капитализации процентов.
Решение: m = 365. По формуле (1.6) получим:
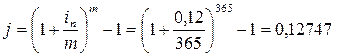
Практические задания:
1. Срок платежа по векселю составляет 6 месяцев. Эффективность операции учета в банке должна составить 120 % годовых. Определить эквивалентное значение учетной ставки.
2. Банк хочет обеспечить себе доходность 90 % годовых. Какую он должен определить учетную ставку, если до погашения векселя осталось 8 месяцев?
Источник
Эквивалентные процентные ставки
Для нахождения эквивалентных процентных ставок используют уравнения эквивалентности.
P (1 + ni) = P/ (1 — nd) или (1 + ni) = 1 / (1 — nd),
т.е. необходимо приравнять соответствующие коэффициенты наращения.
Отсюда d = i / (1 + ni) и i = d / (1 — nd).
Срок уплаты по долговому обязательству — полгода, простая учетная ставка — 18%. Какова доходность данной операции, измеренная в виде простой ставки ссудных процентов?
i = 0.18 / (1 — 0.5 х 0.18) = 0.198 = 19.8%.
Для нахождения эквивалентности между собой годовой сложной ссудной ставки и годовой сложной номинальной ссудной ставки приравняем выражения: S = P (1 + Іс)п и S = P (1 + j/m)mn, т.е. (1 + Іс)п = (1 + j/m)mn.
Отсюда Іс = (1 + j/m) m — 1.
Полученная годовая ставка сложных процентов, эквивалентная номинальной процентной ставке, называется эффективной ставкой сложных процентов. Ее необходимо знать для определения реальной доходности или сравнения процентов, когда используются разные интервалы начисления.
Рассчитать эффективную ставку сложных процентов, если номинальная ставка 24% и начисление процентов ежемесячное.
іс = (1 + 0.24 / 12)12 — 1 = 0.268 = 26.8%.
Определить, под какую ставку процентов выгоднее поместить капитал в 10 000 тыс.
а) под простую ссудную ставку 20% годовых;
б) под сложную ссудную ставку 12% годовых при ежеквартальном начислении процентов.
Здесь не обязательно считать величину наращенной суммы при различных ставках. Поэтому не важна величина первоначального капитала. Достаточно, например, найти простую процентную ставку, эквивалентную данной сложной ставке, т.е. использовать формулу
і = [(1 + j / m)mn — 1] / n = [(1 + 0.12 / 4)20 — 1] / 5 = 0.1612 = 16.12%.
Поскольку простая процентная ставка 16.12%, которая дала бы одинаковый с данной сложной процентной ставкой (12%) результат, значительно ниже предложенной в первом варианте ставки (20%), ясно, что гораздо выгоднее первый вариант вложения (под простую ставку 20% годовых).
Посчитаем теперь наращенные суммы в обоих случаях:
а) S = 10 000 (1 + 5 х 0.2) = 20 000 тыс. р.;
б) S = 10 000 (1 + 0.12 / 4)20 = 18 061 тыс. р.
Полученный результат подтверждает ранее сделанный вывод о том, что первый вариант более выгоден, поскольку дает большую сумму наращения. При этом использование эквивалентных ставок вдвое сокращает расчеты.
Вексель учтен за три месяца до срока его погашения по учетной ставке 20% годовых. Определить значение эквивалентной ставки простых процентов, определяющей доходность операции учета.
Простая ставка процентов равна 20% годовых. Определить значение эквивалентной ей учетной ставки при выдаче ссуды на полгода.
Кредит на два года предоставлен по ставке сложных процентов 16% годовых. Определить значение эквивалентной учетной ставки при выдаче ссуды на полгода.
По депозитному сертификату сроком на пять лет начисляются простые ссудные проценты по ставке 15% годовых. Определить эквивалентную ставку сложных процентов.
Банк ежемесячно начисляет проценты на вклады по номинальной годовой ставке 12% годовых. Определить доходность вкладов по сложной годовой ставке процентов.
Можно сделать следующие выводы:
Значение эффективной ставки больше значения номинальной, а совпадают они при m = 1.
Простая учетная ставка всегда меньше эквивалентных ей других ставок (поскольку наращение по этой ставке при прочих равных условиях всегда быстрее).
Эквивалентность различных процентных ставок не зависит от величины первоначальной суммы Р (первоначальная сумма предполагается одинаковой).
Эквивалентность процентных ставок всегда зависит от продолжительности периода начисления процентов за исключением случаев эквивалентности между собой сложных процентных ставок разного вида (если период начисления один и тот же).
Источник
Эквивалентность процентных и учетных ставок
Определение эквивалентной ставки.
Финансовые операции (ставки) называются эквивалентными, если они дают один и тот же результат.
Вычисление простой учетной ставки, которая эквивалентна заданной простой процентной ставке:
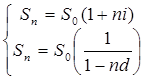
Пример 3.1. Необходимо определить значение простой учетной ставки, эквивалентной простой ставке процентов, равной 10%, если n=10.
3,2,Вычисление простой процентной ставки,
эквивалентной простой учетной ставке:
Пример 3.2. Какова доходность, измеренная в виде ставки простых процентов (K=365 дней), учета векселя по учетной ставке 10% ( 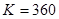
3.3.Эквивалентность простых ставок при разных временных базах K=365 для простых процентов, 

Пример 3.3. Операция учета должна принести 30% дохода (в расчете на год). Срок ссуды 55 дней. K=365 для простых процентов. Найти эквивалентную простую учетную ставку (K=360).
3.4.Вычисление простой процентной ставки, эквивалентной заданной сложной процентной ставке:

Пример 3.4. Ссуда выдана под 20 сложных годовых процентов. Каков должен быть уровень простой процентной ставки при сроке: а) 10 лет, б) 8 месяцев?
Ответ: 51,92%; 19,39%.
3.5.Вычисление сложной процентной ставки, эквивалентной простой процентной ставке:
Пример 3.5. Какой годовой ставкой сложных процентов можно заменить в контракте простую ставку в 18%, не изменяя финансовых отношений сторон? Срок операции 580 дней.
3.6.Вычисление сложной процентной ставки, эквивалентной простой учетной ставке.

Пример 3.6. Какова эффективность, выраженная в годовой сложной процентной ставке, дисконтирования векселя по простой учетной ставке 8%? Срок оплаты векселя наступит через 120 дней. (Временные базы по умолчанию).
3.7.Вычисление номинальной процентной ставки, эквивалентной заданной эффективной процентной ставке:

Пример 3.7. При разработке соглашения стороны договорились о том, что действительная доходность финансовой операции должна составить 9%, причем начисление процентов будет осуществляться помесячно. Найти номинальную ставку процентов.
3.8+.Вычисление годовой сложной процентной ставки, эквивалентной заданной непрерывной ставке процентов:
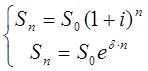
Пример 3.8. Множитель наращения при дискретно изменяющихся непрерывных процентах составил 2,5345 при n=10 лет. Найти эквивалентную годовую ставку сложных процентов.
3.9. Вычисление средних простых процентных ставок:
Пример 3.9. В контракте предусматривается начислять простые проценты в следующих размерах
| Период |  | 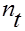 (в годах) (в годах) |  |
| 0,10 | 0,5 | 0,05 | |
| 0,12 | 1,0 | 0,12 | |
| 0,15 | 0,5 | 0,075 | |
| 2,0 | 0,245 |
Найти эквивалентную среднюю простую процентную ставку и наращенную сумму, если S0=10 тыс. руб.
Ответ: 12,25%; 12,45 тыс.руб.
3.10. Вычисление сложных средних процентных ставок:
Пример 3.10. Процентная ставка по ссуде определена на уровне 8,5% плюс маржа 0,5% в первые два года, 0,75% в следующие три года. Найти среднюю ставку.
3.11. Финансовая эквивалентность обязательств.
Определение. Финансовые изменения называются эквивалентными, если после изменений условий, платежи, приведенные к одному моменту времени, окажутся равными.
Пример 3.11. Имеются два обязательства. Условие первого: 



Ответ: 387,10 тыс.руб.; 390,70 тыс. руб.; неэквивалентны.
3.12. Консолидирование задолженностей при простой процентной ставке.
Определение. Консолидирование задолженностей означает приведение этих задолженностей к одному моменту времени.
Пример 3.12. Решено консолидировать 3 платежа со сроками 15.05, 15.06, 15.08, суммы платежей 10 тыс. руб., 20 тыс. руб., 15 тыс. руб. Ставка простых процентов равна 8%. Найти консолидированную сумму к 01.08.
3.13.Консолидирование платежей при простой учетной ставке.
Пример 3.13. Два векселя со сроками 10.06 на 10 тыс. руб. и 01.08 на 20 тыс. руб. заменяются одним с продлением срока до 01.10. При объединении векселей применена простая учетная ставка 8%. Сроки пролонгации составят 113 и 61 день.


Последнее изменение этой страницы: 2017-03-14; Просмотров: 3783; Нарушение авторского права страницы
Источник