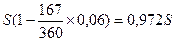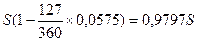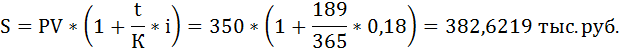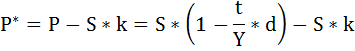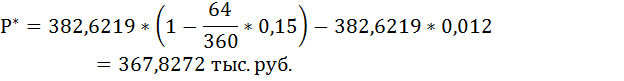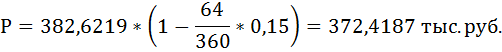Определить доходность операции учета векселя по эффективной ставке простого процента

Покупка и продажа векселя с использованием простой учетной ставки

Доходность этой финансовой операции связана с разностью цен купли-продажи, которая зависит от сроков погашения векселя и уровнем учетных ставок в момент купли-продажи векселя. Обозначим S – номинал векселя, d₁ – учетная ставка, по которой его учел банк за время t₁ до его погашения. Тогда цена покупки P₁ банком равна P₁ = S (1- d₁ t₁).

Банк продал вексель за время t₂ до его погашения по ставке d₂. Цена продажи P₂ равна P₂ = S (1- d₂ t₂).

Таким образом, вексель куплен по цене P₁ и продан по цене P₂ через срок (t₁-t₂) дней. Доход от купли-продажи векселя равен P₂ — P_1.

Эффективность операции за срок (t₁-t₂) выражается в виде процентной ставки i:

i = .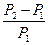

Подставляя в эту формулу соответствующие значения для P₁ и P₂ получаем доходность за срок t₁-t₂

i = .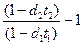

Зная доходность за (t₁-t₂) дней можно рассчитать годовую эффективную ставку простых или сложных процентов.

Пример 33.

Вексель куплен за 167 дней до его погашения, при покупке использована учетная ставка 6%. Через 40 дней его реализовали по учетной ставке 5,75%. Определить эффективность операции купли-продажи. (К=360 дней).

Вексель куплен за 167 дней по цене P₁ .

P₁ =

За 127 дней до его погашения вексель продан по цене

P₂ =

Доходность операции за 40 дней составила

i = %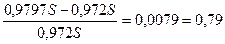

Доходность операции, выраженная годовой ставкой простых процентов равна:

i_эф = %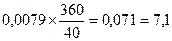

Доходность операции, выраженная годовой ставкой сложных процентов равна:

i_эф.сл. = %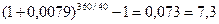

Эти процентные ставки эквивалентны и показывают равную доходность финансовой операции.

Покупка и продажа финансового инструмента,

Приносящие проценты

При покупке-продаже финансового инструмента доход образуется за счет разницы цен купли-продажи, которые зависят от процентных ставок в момент купли-продажи. Для оценки доходности также используется эффективная процентная ставка.

Цена покупки Р₁ определяется на основе дисконтирования по процентной ставке i₁:

Цена продажи Р₂ определяется дисконтированием по процентной ставке i₂:

Доходность операции купли-продажи за срок t₁ — t₂ равна:

i = .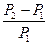

Зная доходность за срок (t₁ — t₂) дней можно определить годовую процентную ставку.

Пример 34.

Депозитный сертификат номиналом 100 тыс.руб., выпущенный на год с начислением простых процентов по ставке 20% годовых, куплен за 180 дней до его погашения и продан через 30 дней. Ставки простых процентов в моменты покупки и продажи составляли 12% и 10% соответственно. Определить доходность операции купли-продажи в виде эффективной ставки простых и сложных процентов

К концу срока цена сертификата составит 100000 (1 + 0,2 · 1) = 120000 (руб.). Поскольку сертификат куплен за 180 дней до его погашения, то его цена покупки Р₁ = 120000 / (1 + 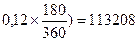(руб.)

Цена продажи равна Р₂ = 120000 / (1 + 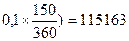(руб.)

Доходность за 30 дней равна: i = %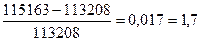

Годовая ставка простых процентов i_эф. = %.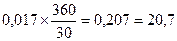

Годовая ставка сложных процентов i_эф.сл. = %.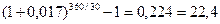

Контрольные вопросы

1. Какие виды доходов может получать банк от ссудных и учетных операций?

2. Дайте определение эффективной ставки процентов.

3. Как рассчитать годовую эффективную ставку, если известна доходность за срок финансовой операции?

4. От каких факторов зависит доходность купли-продажи финансовых инструментов?

Источник

Задача №25. Расчёт общего дохода банка от операции вексельного учёта

12 февраля 2015 г. составлен вексель, по которому 20 августа 2015 г. векселедатель обязан уплатить владельцу векселя сумму в размере 350 тыс. руб. вместе с процентами, начисленными по простой ставке 18% годовых (К=365).

Получатель векселя учел его в банке 16 июня 2015 г.

Для учета векселя банк применил простую учетную ставку 15%, германскую практику начисления процентов от полной стоимости векселя и взыскал комиссионные в размере 1,2% от полной стоимости векселя.

Рассчитайте:

— сумму, полученную предъявителем векселя,

— сумму дисконта и

— общий доход банка от операции учета.

Решение:

1. Будущую стоимость векселя к погашению рассчитаем по формуле:

S – наращенная сумма,

PV – исходная (современная – present value) стоимость векселя,

t – срок операции (12 февраля 2015 г. по 20 августа 2015 г. прошло 190 дней; первый и последний день финансовой операции берётся за 1, поэтому t = 189),

К – продолжительность года,

i – ставка процентов за период.

Векселедатель обязан уплатить владельцу векселя 382,6219 тыс. руб.

2. Сумму, полученную предъявителем векселя после учёта, определим по формуле:

Р — дисконтированная величина,

d — учётная ставка,

k – комиссионный процент от полной стоимости векселя.

Германская практика предполагает приближённое измерение числа дней операции и приближённое измерение продолжительности года Y = 360.

Продолжительность каждого месяца принимаем за 30 дней:

июнь – 15 дней, (с 16 по 30 июня)

август – 20 дней (с 1 по 20 августа).

Первый и последний день финансовой операции берём за 1, поэтому t = 64

Сумма дисконта равна разности между суммой по векселю и ценой его покупки банком.

D = 382,6219 – 372,4187 = 10,2033 тыс. руб.

Общий доход банка от операции учета будет состоять из дисконта и суммы комиссии:

I = 10,2033 + 382,6219 * 0,012 = 14,7947 тыс. руб.

Источник

Доходность векселя

Вы будете перенаправлены на Автор24

Как рассчитывается доход по векселю

Вексель как ценная бумага может принести доходу тому, кто этот вексель приобретает (векселедержателю, кредитору). Однако, чтобы выгодно вложить средства в покупку векселя необходимо рассчитывать возможный доход.

Так доход по векселю можно получить в следующих формах:

• в качестве процентов, которые будут начислены за вексель;
• как дисконт (тогда дисконт будет представлять разность между суммой по векселю и суммой долга по векселю).

В первом случае формула для расчета дохода выглядит так:

• где Дв – доход по векселю процентному;
• Вс – номинальная сумма векселя;
• С – процентная ставка (выражается в долях).

Рассмотрим формулу расчета дохода по второй форме векселя:

Помощь со студенческой работой на тему
Доходность векселя

$Дв = Вс – Цп$, где Цп – цена покупки векселя

$Дв = Цпр – Цп$, где Цп р – цена продажи векселя.

Кроме дохода от векселя также рассчитывается и доходность векселя. Рассмотрим формулы для расчета.

Как рассчитывается доходность по векселю

Так как срок оборота векселя обычно составляет срок меньше года или год. То формула для расчета выглядит так:

$S = Bc \cdot ( 1 + (n/(N\cdot 100)) \cdot С)$

• где S – сумма, которая будет получена по векселю;
• Вс — номинальная сумма векселя;
• n – срок обращения векселя, выраженный в днях;
• С — процентная ставка (выражается в долях);
• N – количество дней в году;

Такой метод, основанный на точных процентах, предполагает, что количество дней в год составляет 365 или 366 (високосный год). Однако используется еще и метод, основаны на простых процентах, когда количество дней в год принимается за 360 дней, а количество дней в месяце берется за 30 дней.

Есть еще одна формула для расчета доходности. Дисконтная доходность определяется по следующей формуле:

$rд = (D/Nц) \cdot (360/T)$

• где rд – это доходность векселя или дисконтная ставка;
• D – величина дохода процентного;
• Nц – номинальная цена погашения векселя;
• Т – количество дней, оставшееся до погашения денежных средств по векселю;

Пример расчетов доходности по векселю

Рассмотрим пример расчета.

Предположим, что компания приняла решение выпустить векселя. Необходимо вычислить цену размещения такого векселя, если сумма, на которую выписывается такой вексель составляет 150 рублей, срок платежа составляет 250 дней, а ставка составляет 17 %.

Таким образом, получим следующее:

необходимо преобразовать формулу, так как необходимо найти неизвестное – S.

Преобразовав формулу, получим следующее: 150 рублей / (1 +(250 дней/(360 дней $\cdot$ 100)) $\cdot$ 17 %) = 134, 16 рубля

Рассмотрим еще один пример.

Вексель продается на рынке за сумму в 19 000 рублей. В срок погашения, в период, равный 120 дням, должна будет выплачена сумма по векселю в размере 20 000 рублей. Найдем доходность векселя по условиям задачи.

rд = ((20 000 рублей – 19 000 рублей)/ 20 000 рублей) $\cdot$ (360 дней/120 дней) = 0, 15 или 15 %.

То есть доходность векселя при таких условиях составляет 15 %.

Итак, в зависимости от формы выпуска рассчитывается и доходность. На предприятиях, занимающихся операция с такими ценными бумагами, разрабатываются системы анализа доходности векселей с использование программных средств обеспечения, в том числе MS Excel. Для этого создаются специальные шаблоны, удобные для представления результата и расчетов. Примера такого шаблона для расчета доходности представлен на рисунке 1 ниже.

Для того, чтобы вычислить доходность в предложенном шаблоне, необходимо ввести следующие значения в ячейки В16 и В17. Итак, в $В16 =ДОХОДСКИДКА(E4;B5;E16;B12;E7)$, а в $В17 = (B12/E16)$ ^ $(365/(B5-E4)) -1.$

Предварительно вводятся в ячейки необходимые доступные данные для вычислений.

Для того чтобы рассчитать доходность по предложенному выше шаблону, необходимо знать значения даты заключения сделки и даты погашения, сумму сделки, процентную ставку в случае отсрочки платежа.

Источник

Оценка прибыльности векселей

Расчет доходности векселей

В зависимости от вида финансовой сделки векселя подразделяются на:

— финансовые (отражают отношения займа денег);

— товарные (в его основе лежит сделка по купле-продаже).

Продавец поставляет покупателю товар, получает от последнего обязательство уплатить через определенное время стоимость товара и проценты за отсрочку платежа. Общий итог оплаты единой вексельной суммой фиксируется в документе.

Держатель векселя может хранить долговое обязательство до даты погашения, а затем предъявить к оплате. Однако при недостатке денежных средств владелец товарного векселя может продать документ банку и получить вексельную сумму за вычетом дисконта в пользу банка. Эта операция называется учетом векселей.

S – вексельная сумма;

P – приведенная величина вексельной суммы:

i – учетная ставка; g – количество дней до погашения векселя;

К – количество дней в году.

Банк может осуществлять учет нескольких векселей в счет некоторой суммы долга. Учет такого портфеля векселей производится одновременно, а погашение равномерно во времени. Как правило, очередной вексель погашается векселедержателем через полгода. Данная операция называется учетом портфеля векселей (форфетной).

Условия форфейтной сделки: у покупателя товара нет денег, а продавец не может продать товар в кредит и настаивает на немедленной оплате. Противоречие разрешается так: покупатель выписывает комплект векселей на сумму, равную стоимости товара плюс проценты за кредит. Сроки векселей с определенным шагом распределены во времени. После получения портфеля векселей продавец сразу учитывает его в банке, получая деньги. Таким образом, кредитором покупателя выступает банк. Кредитуя сделку, банк имеет дисконт в свою пользу, определяемый процентом за кредит.

Цель форфейтной сделки:

— для покупателя: приобретение товара в кредит, за что сверх цены товара уплачивает проценты за кредит;

— для продавца: получение при учете вексельной суммы, равной цене товара;

— для банка: получение дохода в виде дисконта от учета векселей.

Цели реализуется следующим образом:

1) определение исходных данных;

2) выбор варианта начисления процентов за кредит (на остаток долга или на всю сумму долга);

3) разработка плана погашения портфеля векселей. В плане по периодам начисления указываются: сумма уплаты за товара (равными частями), проценты за кредит и вексельная сумма. Сумма каждого векселя складывается из части суммы долга и процентов за оплату товаров в кредит.

P –цена товара в счет которого выписан портфель векселей;

iп – процентная ставка за период;

t – номер периода (векселя);

n – число векселей в портфеле;

(1 – (t — 1) / n) – множитель, учитывающий продолжительность периода оставшегося до полного погашения долга.

С возрастанием порядкового номера векселя до погашения всего портфеля остается меньше времени, и %-ы, начисленные на остаток долга, уменьшаются как вследствие сокращения долга, так и времени кредита

С увеличением порядкового номера векселя сумма %-тов за кредит увеличивается

Вексельная сумма по такому векселю: Рв = (Р / n ) + I .

4) Оценка доходности сделки с позиции каждого участника:

5) Корректировка исходных данных.

Если Рпр меньше фактической цены товара Р, то увеличиваются цена товара или проценты за кредит:

к – коэфф. корректировки: к = Р / Рпр

Задача по определению вексельной суммы с решением

Источник