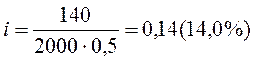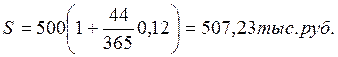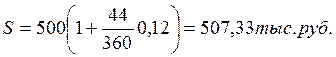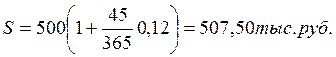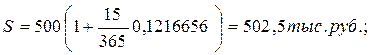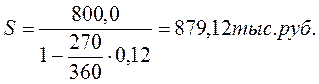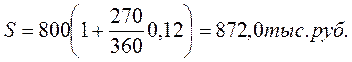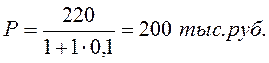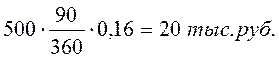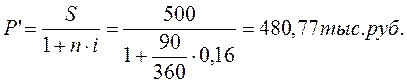Определить доходность этой сделки т е размер процентной ставки

Как посчитать доходность облигаций?

Я хочу попробовать вложиться в облигации, но раньше пользовался только вкладами. Там все понятно, ставка указана в договоре.

В облигациях все выглядит сложнее. Расскажите, пожалуйста, как правильно посчитать доходность по облигации. Она зависит только от размера купона или нет?

Облигации — полезный вид ценных бумаг: доход по ним выше, чем по вкладам. Однако сами по себе эти ценные бумаги сложнее. Давайте разбираться, какие бывают виды доходностей, от чего зависит их величина и как это все посчитать.

Типы облигаций по форме выплаты

Чаще всего встречаются купонные облигации. Купон — это выплата процентов, которая происходит с определенной периодичностью: например, раз в полгода. Даты выплат известны заранее, а вот размер купонов может со временем меняться.

Также бывают дисконтные ценные бумаги: по ним не выплачиваются купоны, но сами бумаги продаются заметно дешевле номинала. Доход можно получить, если цена вырастет или если погасить облигацию по номиналу в конце срока.

Облигации с купоном популярнее, поэтому рассмотрим их на примере типичного представителя — ОФЗ-26217 с погашением 18 августа 2021 года. По состоянию на 2 октября эта облигация стоит 99,3% от номинала, то есть 993 рубля.

Купонная доходность

Это деньги, которые эмитент обязан периодически платить владельцам облигаций. Процентную ставку доходности облигации с купоном посчитать легко:

(Годовые купоны / Номинал) × 100%

Номинал облигации ОФЗ-26217 — 1000 рублей, выплаты производятся каждые полгода в размере 37,4 рубля. Купонная доходность — 7,5% в год.

Облигации далеко не всегда продаются по номиналу: их цена меняется со временем. Поэтому расчет купонной доходности не позволяет точно узнать, сколько инвестор заработает на облигациях.

Текущая доходность

Это более точный показатель, при расчете которого используется не номинал, а чистая цена, — без накопленного купонного дохода. НКД — это часть купона, которая накопилась, но еще не выплачена. Покупая облигацию, нужно заплатить ее владельцу НКД — это как компенсация за то, что он продает ценную бумагу, не получив купон. Зато новый владелец получит весь купон в дату выплаты.

Величина текущей ставки показывает, какой денежный поток дает облигация, купленная по определенной цене.

Формула выглядит так:

(Купонный доход за год / Чистая цена) × 100%

Доходность ОФЗ-26217 равна (74,8 / 993) × 100%, или 7,53% годовых.

Этот показатель выше купонной ставки, так как цена ОФЗ-26217 ниже номинала. Если бы эта ОФЗ стоила дороже номинала, текущая доходность была бы ниже купонной.

Простая доходность к погашению

Многие держат облигации до даты их погашения, когда вместе с последним купоном инвестор получает номинал. Но рассчитать величину доходности облигации на момент погашения можно лишь тогда, когда известен размер всех купонов.

Ставка к погашению рассчитывается по более сложной формуле:

((Номинал − Полная цена покупки + Все купоны за период владения) / Полная цена покупки) × (365 / Количество дней до погашения) × 100%

У ОФЗ-26217 простая доходность к погашению составит ((1000 − 1001,2 + 224,4) / 1001,2) × (365 / 1051) × 100% = 7,74% годовых.

Эффективная доходность к погашению

Если использовать полученные купоны для покупки дополнительных ценных бумаг, можно посчитать ставку дохода по облигациям с реинвестированием купонов — примерно как вклад с капитализацией процентов.

Считается, что купоны вкладываются в новые бумаги по текущей ставке — той, что была первоначально. Это допущение, так как цена меняется со временем и фактическая доходность будет отличаться.

Реинвестировать купон можно, если полученного дохода от купонов хватает на покупку дополнительных ценных бумаг. Получив 37,4 рубля в виде купона по одной ОФЗ-26217, часть облигации федерального займа купить не удастся. А вот если иметь 100 таких бумаг, купонная выплата будет 3 740 рублей. Этого хватит на 3 дополнительные ценные бумаги — и еще останется.

Простой и точный способ узнать эффективную доходность к погашению — воспользоваться облигационным калькулятором на сайте Rusbonds или на сайте Московской биржи. У ОФЗ-26217 этот показатель на 2 октября был равен 7,93% годовых.

Для расчета доходности с помощью облигационного калькулятора необходимо выбрать ценную бумагу из списка, указать дату приобретения и чистую цену без НКД. Калькулятор также покажет текущую и простую процентные ставки к погашению, то есть их необязательно считать вручную. При этом налоги, брокерские и депозитарные комиссии в калькуляторе не учитываются.

Нюансы и полезные советы

Цена на облигацию зависит в том числе от процентных ставок в экономике. Если Центробанк поднимет ставку, инвесторы захотят иметь инструменты с большей доходностью. Они начнут распродавать старые бумаги с постоянным купоном, и те подешевеют. Если ЦБ снизит ставку, на старые облигации вырастет спрос и они подорожают. Чем меньше времени до даты погашения, тем менее чувствительны ценные бумаги к изменениям ключевой ставки.

Выбирая между бумагами государственных займов и корпоративными, важно знать, что наибольшая доходность при прочих равных — у корпоративных облигаций. Более щедрые купоны по сравнению с государственными — это премия за риск потерять вложенные деньги, если дела у компании пойдут плохо. Если у бумаги необычно большие купоны или цена упала намного ниже номинала, значит, велики шансы лишиться денег.

Купонный доход по одним корпоративным облигациям облагается НДФЛ, по другим — нет. Список бумаг со льготным налогообложением можно посмотреть на сайте Московской биржи. Сравнивая доходность ОФЗ, корпоративных бумаг и вкладов, помните про НДФЛ.

С полученного вами НКД могут удержать налог. Лучше продавать облигацию, когда по ней выплачен купон или НКД минимальный. Также налог взимается, если продать облигацию дороже цены покупки или купить ее дешевле номинала и дождаться погашения по номиналу.

Простой вариант увеличить доход от вложений — открыть ИИС и использовать вычет на взносы. Возврат НДФЛ повысит доходность инвестиций на несколько процентных пунктов в год, а вычет можно внести на ИИС и купить дополнительные активы.

Хорошо, если брокер разрешает получать купоны на банковский счет, а не зачисляет их на ИИС. Тогда купоны можно будет самостоятельно внести на ИИС и получить потом вычет и с этих денег.

Если у вас есть вопрос о личных финансах, правах и законах, здоровье или образовании, пишите. На самые интересные вопросы ответят эксперты журнала.

Источник

Сущность процентных платежей

Тема: Простые проценты

Сущность процентных платежей

Слово «процент» как экономическое понятие в значении «прибыль», «выгода», «преимущество» стало использоваться во второй половине 19 века.

Финансовое определение процента – плата, которую одно лицо (заемщик) передает другому лицу (кредитору) за то, что последний предоставляет первому во временное пользование денежные средства. В современной финансовой лексике процент определяется как плата за использование заемных средств, как цена рентных доходов.

В бизнес-лексике – работать за проценты означает работать за вознаграждение, исчисляемое в зависимости от прибыли или оборота.

Процент и его основные формы:

П л а т а предпринимателя (заёмщика) за заёмный капитал:

КОМУ

Ссудный процент º процентная ставка.

Процентная ставка характеризует доходность кредитной сделки для кредитора и стоимость кредита для заёмщика. Она показывает, какая доля от суммы выданного кредита будет возвращена владельцу капитала в виде дохода. Поэтому процентная ставка рассчитывается как отношение дохода, полученного за определенный период (чаще всего за год), к величине капитала, предоставляемого в кредит. Величина процентной ставки определяется отношением:

(1.1)

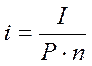
где i – процентная ставка, выраженная в долях единицы (десятичной дробью);

I – величина дохода владельца капитала;

Р – сумма капитала, предоставляемого в кредит;

n – срок ссуды в годах.

Пример 1.1.

Фирма приобрела в банке вексель, по которому через год должна получить 66,0 тыс.руб. (номинальная стоимость векселя). В момент приобретения цена векселя составила 60 тыс.руб.

Определить доходность этой сделки, т.е. размер процентной ставки.[Номинальная стоимость векселя =
Цена продажи векселя * (1 + (срок векселя * ставка / 365*100)) ]

По условию задачи первоначальная сумма капитала, предоставляемого в кредит, P=60,0 тыс.руб., номинальная сумма векселя S=66 тыс.руб., доход векселя

I=66-60=6 тыс.руб.

Отсюда

Таким образом, на каждые вложенные в вексель 1000 руб. фирма получит доход в размере 100,0 руб.

Пример 1.2.

Коммерческий банк приобрёл на 2,0 млн.руб. государственных облигаций со сроком погашения через 6 месяцев. По истечении указанного срока банк рассчитывает получить по облигациям 2140 тыс.руб. Определить доходность ГКО.

I=2140-2000=140 тыс.руб.

Используя выражение для расчёта процентной ставки, мы можем записать, что величина дохода определяется по формулам:

(1.2) (Здесь процентная ставка выражена в процентах)

(1.3)

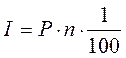
Величину I часто называют процентным доходом, а иногда просто процентами.

В практике используются различные методы начисления процентов. Основное их различие сводится к определению исходной суммы (базы), на которую начисляются проценты. Эта сумма может оставаться постоянной в течение всего периода или меняться; в зависимости от этого различают следующие методы начисления процентов:

· по простым процентным ставкам;

· по сложным процентным ставкам;

Сущность метода начисления по простым процентным ставкам сводится к тому, что проценты начисляются в течение всего срока кредита на одну и ту же величину капитала, предоставляемого в кредит.

Метод начисления по сложным процентным ставкам заключается в том, что в первом периоде начисление производится на первоначальную сумму кредита, затем она суммируется с начисленными процентами и в каждом последующем периоде проценты начисляются на уже наращённую сумму. Таким образом, база для начисления процентов постоянно меняется. Иногда этот метод называют «процент на процент».

Другое различие методов начисления процентов заключается в установлении процентной ставки в качестве фиксированной или переменной величины. Так, например, в контракте может быть определена процентная ставка на первый год в одном размере, а на последующие годы предусматривается ее рост (снижение) на определенную величину.

Кроме того, могут применяться «плавающие» ставки, величина которых «привязывается» к темпам инфляции или ставкам рефинансирования, объявляемым Центральным банком, или же ее изменение оговаривается какими-либо другими условиями. Например, в контракте оговаривается первоначальная процентная ставка (базовая ставка), которой пользуются только один период для начисления процентов (допустим, первый квартал), в дальнейшем она будет расти в соответствии с ростом темпов инфляции.

1.2. Вычисление наращённых сумм на основе простых процентных ставок

По условиям кредитного контракта начисленные проценты могут выплачиваться кредитору или по мере их начисления в каждом периоде, или совместно с основной суммой долга по истечении срока контракта. В последнем случае сумма, получаемая кредитором, называется наращённой суммой.

Таким образом, наращенная сумма есть результат сложения суммы, предоставляемой в кредит, и начисленных процентов.

Формула определения наращенной суммы с использованием простых процентов (формула простых процентов) может быть записана в следующем виде:

S= P+I= Р + P*n*i = P(1+n*i), (1.4)

где S— наращённая сумма;

значения символов Р, п, i даны при записи формул (1.1)—(1.3).

Выражение (1+n*i) называется множителем наращения простых процентов.

Пример 1.3.

Банк выдал районной администрации ссуду в размере 4,0 млн руб. сроком на 2 года по ставке простых процентов, равной 11% годовых.

Определить проценты и сумму накопленного долга (наращённую сумму).

По условию: Р= 4,0 млн; i= 0,11; n = 2 года;

I=4,0*2*0,11 =0,88 млн руб.;

S= 4,0 + 0,88 = 4,88 млн руб.

или по формуле (1.4)

S=4*(1+2*0,11)= 4,88 млн руб.

Пример 1.4.

Банк выдал кредит 18 января в размере 500,0 тыс. руб. Срок возврата кредита — 3 марта; процентная ставка — 12,0% годовых; год невисокосный. Определить сумму долга, подлежащую возврату. Необходимо рассчитаем се тремя методами.

Точное число дней ссуды определим по табл. 1 (Приложение 1): 62–18=44 дня.

Такой же результат мы получим, рассчитывая число дней по календарю;

С 18.01 по 31.01 включительно— 14дней;

февраль — 28 дней;

t=45-1=44 дня.

Приближенное число дней ссуды (продолжительность каждого месяца принимается за 30 дней):

январь — 13 дней;

февраль— 30 дней;

t=46-1=45 дней.

Возможные варианты расчета наращенной суммы:

1) по точным процентам с точным числом дней ссуды:

2) по обыкновенным процентам с точным числом дней ссуды:

3) по обыкновенным процентам с приближенным числом дней ссуды:

Приведенный пример свидетельствует, что для кредиторов наиболее предпочтительным является третий вариант начисления процентов.

Между величинами процентного дохода, рассчитанными с использованием различной временной базы (I₃₆₀ и I₃₆₅) при равном числе дней ссуды (t) существуют следующие соотношения:

И . (1.6)

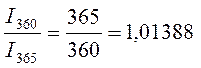
Данные соотношения характеризуют зависимость величины процентного дохода от выбранной временной базы.

По данным примера 1.4(2).

I₃₆₀=507,33-500=7,33тыс.руб I₃₆₅=507,23-500=7,23тыс.руб

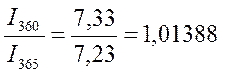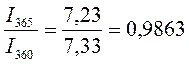Эти соотношения также могут быть использованы при определении эквивалентных процентных ставок, т.е. ставок, приносящих одинаковые процентные доходы при различных временных базах, но равных первоначальных капиталах: ;

Пример 1.5.

При выдаче ссуды 500,0 тыс. руб. на 15 дней по ставке 12% годовых, при К=360 дней, наращённая сумма и процентный доход соответственно составят:

Определить величину процентной ставки, обеспечивающей такой же процентный доход при временной базе К = 365 дней:

i₃₆₅=1,01388*0,12=0,1216656

Проверим это вычисление:

Как указывалось ранее, при заключении кредитного соглашения может быть установлена постоянная на весь период процентная ставка или изменяющаяся (переменная) процентная ставка. При установлении переменной процентной ставки, т.е. дискретно изменяющейся во времени ставки, наращенная сумма определяется по формуле

(1.8)

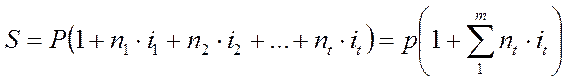
Где i_t — ставка простых процентов в периоде t;

n_t — продолжительность начисления ставки i_t ;

m — число периодов начисления процентов.

Пример 1.6.

Банк предлагает вкладчикам следующие условия по срочному годовому депозиту: в первое полугодие процентная ставка 12,0% годовых, каждый следующий квартал ставка возрастает на 0,5%, Проценты начисляются только на первоначально внесенную сумму вклада.

Определить наращённую за год сумму, если вкладчик поместил в банк на этих условиях 400,0 тыс. руб.:

Решение:

Пример 1.8.

Клиент обратился в банк за кредитом в сумме 800,0 тыс. руб. на срок 270 дней. Банк согласен предоставить кредит на следующих условиях: заёмщик выдаст вексель, обеспечивающий банку доходность от этой операции в размере 12% годовых. Расчет производится с использованием учетной ставки.

Надо определить сумму долга, которая должна будет проставлена в векселе.

Если бы по приведенным данным начисление процентов производилось по простой процентной ставке, то наращенная сумма оказалась бы значительно меньше:

Таким образом, мы убедились, что простая учетная ставка дает более быстрый рост наращенной суммы, чем аналогичная по величине ставка простых процентов.

При равенстве простой процентной ставки (i) и простой учетной ставки (d) различие в величине множителей наращения определяется сроком ссуды, что показано в табл. 1.1.

Пример 1.18.

Через один год владелец векселя, выданного коммерческим банком, должен получить по нему 220 тыс. руб. Какая сумма была внесена в банк в момент приобретения векселя, если доходность векселя должна составить 10% годовых?

Находим современную (текущую)стоимость:

Пример 1.19.

Владелец векселя, номинальная стоимость которого 220 тыс. руб. и сроком обращения 1 год, предъявил его банку для учета за 90 дней до даты погашения. Банк учел его по ставке 12% годовых.

Определить дисконтированную величину (полученную владельцем векселя величину и величину дисконта).

— это сумма, полученная владельцем векселя в результате его учета.

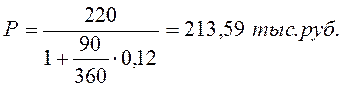
Разность S-P=D’ является дисконтом.

В нашем случае дисконт равен:

D’=220-213,59=6,41 тыс.руб.

Действительно, если бы владелец векселя, получивший после его учета 213,59 тыс. руб., вновь поместил его в банк на 90 дней под 12,0% годовых, то по истечении указанного срока он бы получил 220 тыс. руб.

На практике в подобном случае банк обязательно установит для учета ставку более высокую, чем приведена в примере (12,0%), с целью получения большего дисконта, например 13,0%.

Пример 1.20.

Вексель номинальной стоимостью 500 тыс. руб. был учтен в банке за 90 дней до срока погашения по учетной ставке 16%.

Определить дисконтированную величину векселя, используя антисипативный (предварительный) метод начисления процентов.

Номинальная стоимость векселя — 500 тыс. руб.

Проценты, начисленные на сумму погашения:

Дисконтированная величина 500 — 20 = 480 тыс. руб.

При банковском дисконтировании дисконтированная величина определяется по формуле:

Р’ = S×(1-n·d), (1.44)

где Р’ —дисконтированная величина;

S— наращенная сумма долга;

d— учетная (дисконтная) ставка, выраженная в десятичных дробях;

n — временной интервал от момента учета финансового инструмента до даты уплаты по нему в годах.

По данным предыдущего примера и формуле (1.44) рассчитаем дисконтированную величину:

Величина дисконта равна:

D’=S—Р’=500-480=20тыс.руб.

Дисконтирование с помощью математического и банковского методов, т.е. по процентной ставке i и учетной ставке d, приводит к различным финансовым результатам. Например, если в рассматриваемом примере произвести математическое дисконтирование (i = d = 0.16), то дисконтированная величина будет равна

D’=500-480,77=19,23тыс.руб.

Как видно, при использовании учетной ставки фактор времени учитывается более строго.

В отдельных случаях может возникнуть ситуация, когда совмещаются начисление процентов по ставке i и дисконтирование по ставке d. При этом наращенная величина ссуды будет определяться по формуле:

S=P×(1+n·i)×(1-n’·d), (1.45)

где Р— сумма, предоставленная в кредит;

n — общий срок платежного обязательства;

n’ — срок от момента учета обязательства до даты погашения долга, т.е. n’

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.

Источник