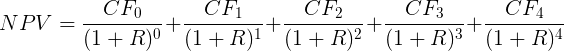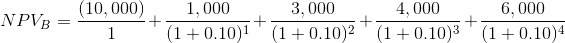Определение npv проекта с инвестициями

Расчет NPV

Понятие NPV

NPV (Net Present Value, ЧДД, чистый дисконтированный доход, чистая приведенная стоимость, чистый приведенный доход) — это такой показатель эффективности инвестиционного проекта, который позволяет суммарно оценить платежи при реализации инвестиционного проекта, приведенные к настоящему моменту времени. Как правило, если значение NPV > 0, то инвестиционный проект считается эффективным, если NPV

Формула расчета NPV

Расчет NPV в общем случае осуществляется по следующей формуле:

Формула расчета NPV

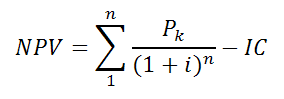
где Рк — величины денежных поступлений в течении n лет;
IC — величина первоначальных инвестиций;
i — ставка дисконтирования.

Возможны варианты, когда реализация инвестиционного проекта связана не с разовыми первоначальными инвестициями, а предполагает инвестирование в течении нескольких периодов. Тогда расчет NPV осуществляется по следующей формуле:

Формула расчета NPV при инвестировании в течении нескольких периодов

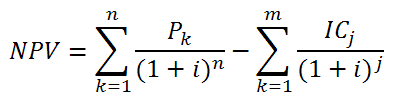
Пример расчета NPV

Приведем пример расчета NPV условного инвестиционного проекта. Предположим, что объем инвестиций в новое здание составляет 15000 тыс.руб.; прогноз ежегодного дохода от сдачи помещений в аренду составляет 5000 тыс.руб. в течении 5-ти лет. Ставка дисконтирования составляет 17%. Рассчитать NPV.

Расчет NPV: NPV = 5000/1.17 + 5000/1.17 2 + 5000/1.17 3 + 5000/1.17 4 + 5000/1.17 5 — 15000 = 15996.73 — 15000 = 996.73 тыс.руб.

Так как рассчитанная величина NPV > 0, то проект может быть принят к практической реализации.

Как уже указывалось ранее, условия инвестирования при реализации проекта могут быть различные. Рассмотрим пример вычисления чистого приведенного эффекта (дохода) в случае, когда вложение средств осуществляется единовременно, а годовые поступления от реализации инвестиционного проекта не равны между собой. Предположим, что объем инвестиций составил 12500 тыс.руб., срок реализации проекта — 5 лет, цена вложенных средств составляет 12,5% годовых, поступления по годам от реализации инвестиционного проекта следующие (в тыс.руб.): 2500; 2250; 1980; 1850; 1720. Определим величину чистого приведенного эффекта: ЧДД = 2500*1,125 -1 + 2250*1,125 -2 + 1980*1,125 -3 + 1850*1,125 -4 + 1720*1,125 -5 — 12500 = -4999,96. Так как значение рассматриваемого показателя меньше 0, то рассматриваемый условный проект не будет приносить прибыли при своем осуществлении и должен быть отвергнут.

Рассмотрим также пример расчета дисконтированного чистого дохода в случае, когда доходы от вложенных средств начинают поступать уже после завершения инвестиционного проекта, т.е. денежный поток включает в себя не только положительные, но и отрицательные величины. Например, имеется инвестиционный проект со следующими показателями потоков платежей (в тыс.руб.): -215; -295; 50; 500; 300; 800; 1000. Цена инвестированного капитала составляет 14% годовых. Вычислим значение чистого приведенного эффекта (дохода): ЧДД = (-215)*1,14 -1 + (-295) *1,14 -2 + 50*1,14 -3 + 500*1,14 -4 + 300*1,14 -5 + 800*1,14 -6 + 1000*1,14 -7 = 834,12. Величина ЧДД положительна, следовательно, проект может быть принят к практическому осуществлению.

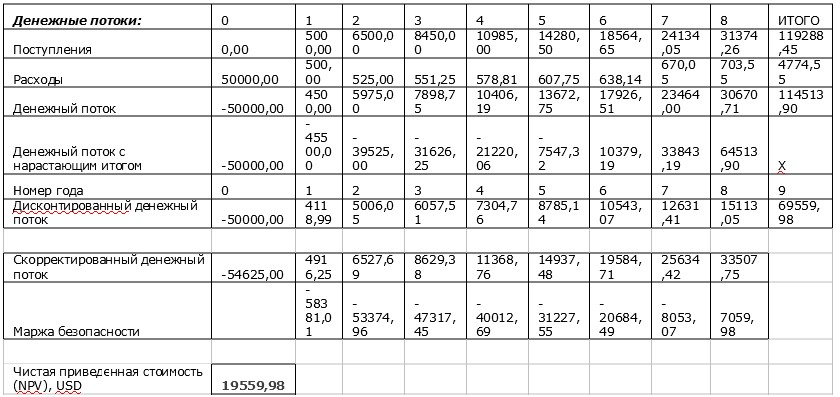
Рассмотрим пример расчета NPV в Excel. Первым шагом вычисления рассматриваемого показателя будет подготовка исходных данных в Excel. Широкий спектр возможностей указанного табличного процессора позволяет исходные данные представить во множестве вариантов (в том числе и с различным оформлением и форматированием), один из которых приведен на рисунке:

Исходные данные для расчета NPV в Excel

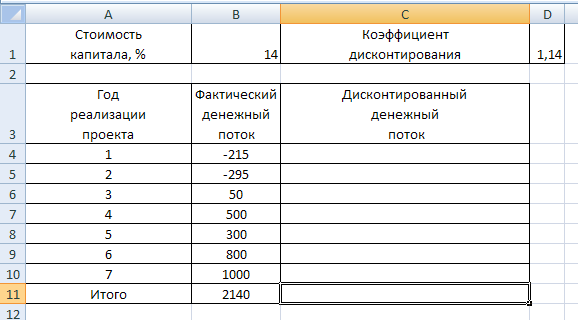
Далее для вычисления чистого приведенного эффекта (дохода) в ячейки C4:C11 необходимо ввести формулы, по котором будет вычислен ЧДД для каждого года реализации проекта. Сделать это можно следующим образом:

Источник

NPV – что это, как рассчитать по формуле

NPV – это суммарная стоимость денежных потоков на определенный момент времени жизненного цикла проекта. Иными словами, это будущий финансовый результат в эквиваленте суммы на текущий момент. Аббревиатура расшифровывается как Net Present Value (чистая приведенная стоимость).

Для расчета NPV используются уже знакомые нам дисконтированные денежные потоки, определяющие доходность инвестиций на любой момент времени. Выполнив предварительный расчет NPV инвестиционного проекта, мы получим примерное представление, сколько денег понадобится на начальном этапе и стоит ли вообще вкладываться в данный проект.

Сегодня мы рассчитаем NPV по формуле и узнаем, как используется метод чистой приведенной стоимости для расчета суммы первоначальных вложений и периода окупаемости проекта.

Что такое NPV

Термин NPV в экономике имеет несколько названий: чистый дисконтированный доход, чистый текущий доход и др. По моему мнению, слово «текущий» только запутывает пользователя, т.к. можно подумать, что это прибыль на данный момент времени. На самом деле, NPV всегда показывает будущий доход, скорректированный на несколько параметров:

С последним пунктом немного сложнее: если процент инфляции еще можно заложить в размере какого-то усредненного значения, то с курсами валют вообще приходится только гадать. Поэтому в наших примерах будем использовать национальную валюту либо иностранную валюту без учета курса.

Вообще расчет чистой приведенной стоимости подразумевает некую стабильность: стабильные денежные потоки примерно с одинаковым темпом прироста, одинаковое значение ставки дисконтирования. Такое, конечно, является редкостью, однако NPV проекта нужен только для «грубых» предварительных расчетов.

Для чего необходим

Метод определения чистой текущей стоимости NPV используется в целях:

• определения стоимости инвестиционного капитала;
• определения размеров поступлений (сколько дохода нужно получить, чтобы этот капитал окупился);
• расчета срока окупаемости.

Нулевое значение показателя NPV говорит о том, что ожидаемых поступлений в процессе реализации проекта будет достаточно для покрытия расходов на инвестиции. Если NPV меньше нуля – проект является убыточным.

Формула расчета

Классическая формула расчета чистой приведенной стоимости выглядит так:

​ \( Pk \) ​ – денежные поступления за n лет;

​ \( i \) ​ – ставка дисконтирования;

​ \( IC (invest capital) \) ​ – сумма первоначальных инвестиций.

Если инвестирование осуществляется по мере развития проекта в несколько этапов, то формула будет такая:

​ \( n \) ​ – количество лет до инвестиций;

​ \( m \) ​ – количество лет после инвестиций;

​ \( j \) ​ – разница между ​ \( m \) ​ и ​ \( n \) ​.

Пример расчета

Выполним расчет NPV по классической формуле на основании исходных данных:

Инвестиционный капитал, руб.	1000000
Срок проекта	4 года
Ожидаемые денежные поступления, руб.	400000
Ставка дисконтирования	15%

Как видим, чистый приведенный доход является положительной величиной. Это означает, что проект себя оправдывает.

Обратите внимание, что под термином «денежные поступления» понимаются чистые денежные потоки, т.е. доходы за минусом расходов, т.к. любой бизнес невозможен без оттока денег.

Что касается ставки дисконтирования, то для ее определения есть несколько вариантов:

1. Если мы анализируем инвестиционный портфель, то в качестве индикатора i обычно берется усредненная доходность по ценным бумагам в стране, где ведется деятельность. Если проект международный – принимается среднее значение доходности по индексам. Далее эта базовая величина уменьшается на ставку по безрисковым активам (чаще всего облигациям).
2. Если капитал выведен из уже существующего бизнеса, то в качестве ставки дисконтирования принимается показатель ROE. Напомню формулу его расчета:

\[ ROE= Чистая\ прибыль/Собственный\ капитал \]

При использовании заемных средств используется ставка по кредиту.

1. Если инвестирование происходит из разных источников (например, часть средств выведена с банковского депозита, а часть – взята в кредит), то ставка дисконтирования рассчитывается исходя из их пропорций. Приведем пример:

​ \( IC \) ​= 37 500 000 руб. (500 000 $ или 14 500 000 грн.) , в т.ч.:

22 500 000 руб. (300 000 $ или 8 700 000 грн.) – средства на депозите под 8%;

15 000 000 руб. (200 000 $ или 5 800 000 грн.) – кредит под 11%.

Но 9,2% – этого недостаточно, поскольку есть еще риск несвоевременных поступлений денег от дебиторов. Поэтому полученное значение следует еще увеличить на размер премии за риск. Для ее вычисления чаще всего используется метод экспертной оценки, основанный на исследованиях аналитиков в разрезе данной отрасли.

Как рассчитать NPV инвестиционного проекта – руководство

Пошаговый алгоритм расчета NPV инвестиционного проекта:

1. Определяем, сколько денег мы готовы вложить на начальном этапе.
2. Примерно рассчитываем размер поступлений за каждый год реализации проекта.
3. Рассчитываем сопутствующие расходы.
4. Определяем ставку дисконтирования, или цену капитала (cost of capital).
5. Рассчитываем дисконтированные денежные потоки по этой ставке.
6. Суммируем полученные значения за все годы.
7. Анализируем результат: если NPV=0 – это означает, что вложенных средств с учетом ожидаемых поступлений будет достаточно. Если величина положительная, значит, проект будет приносить прибыль, и чем выше NPV, тем лучше. Отрицательное значение NPV говорит о том, что проект убыточен.

Как рассчитать NPV в Excel

Приведем пример расчета показателя чистой приведенной стоимости NPV в Excel, используя следующие исходные данные:

• стоимость проекта – 3 750 000 руб. (50 000 $ или 1 450 000 грн.) ;
• прогнозируемые поступления денежных средств: за первый год – 375 000 руб. (5 000 $ или 145 000 грн.) , далее планируется прирост на 30%;
• расходы – 41 250 руб. (550 $ или 15 950 грн.) в первый год, далее увеличиваем их на 5% ежегодно.

Сначала мы посчитаем ставку дисконтирования, используя формулу Фишера. В качестве номинальной ставки возьмем ключевую ставку Центробанка, равную 4,25%. Инфляция составляет 4%.

Мы использовали функцию ЧПС, встроенную в Excel. Если менять значение r, можно определить, что при увеличении ставки дисконтирования NPV проекта снижается. Таким образом, многое зависит от правильности вычисления этого показателя.

Как видим, на шестом году проект при положительном значении NPV начинает приносить прибыль. Сумма отрицательных денежных потоков показывает сумму убытка за текущий год.

Сложности, которые могут возникнуть при расчете

В каких случаях расчет чистой приведенной стоимости NPV может дать ошибочный результат?

1. Неправильное вычисление ставки дисконтирования. Например, если воспользоваться формулой Фишера, как в примере выше, то через пару лет значение ставки ЦБ и уровень инфляции могут измениться и тогда придется выполнять расчет заново.
2. Расчет предстоящих расходов. В зависимости от специфики проекта, расходы могут оказаться существенно выше той суммы, что планировалась на начальном этапе. К примеру, при инвестициях в недвижимость может потребоваться ремонт, закупка оборудования.
3. Расчет доходов. Согласитесь, сложно гарантировать бесперебойное поступление средств от покупателей. Случаются задержки, финансовые затруднения вплоть до банкротства, а на поиск новых клиентов потребуется время.

Итак, при применении метода чистой приведенной стоимости необходимо учитывать все возможные риски. Доходы лучше закладывать на минимальном уровне, а расходы – на максимальном. Ставка дисконтирования должна быть рассчитана по максимуму. Если в этом случае NPV проекта будет положительным – инвестиции с большой вероятностью себя оправдают.

Преимущества и недостатки

Достоинства метода заключаются в следующем:

1. NPV учитывает временной фактор – изменение стоимости денег и длительность жизненного цикла инвестиционного проекта.
2. В немалой степени отражает основные критерии эффективности инвестиций: оценка рисков, расчет срока окупаемости и разницы между доходами и расходами с учетом инфляции.

1. Спрогнозировать денежные потоки непросто – всегда найдутся факторы, которые невозможно принять во внимание заранее.
2. Сложный механизм расчета ставки дисконтирования. Точнее, сложность не в формуле ее расчета, а в выборе правильного метода. Выбрав неподходящий метод, можно получить значение NPV, далекое от истины.

Заключение

Теперь мы знаем, что такое NPV простыми словами, как его можно использовать и какое значение он должен принимать. Мы разобрали примеры расчета, а также достоинства и недостатки метода оценки чистой приведенной стоимости. Несмотря на то, что минусы довольно весомые, NPV является одним из ключевых индикаторов оценки эффективности инвестиций, т.к. он наглядно показывает разницу между суммой денег сейчас и через несколько лет.

Для повышения достоверности результатов анализа рекомендуется провести дополнительную оценку всех возможных рисков, а также ориентироваться на минимальный размер доходов и максимально возможные расходы.

Источник

Расчет NPV

NPV — это сокращение по первым буквам фразы «Net Present Value» и расшифровывается это как чистая приведенная (к сегодняшнему дню) стоимость. Это метод оценки инвестиционных проектов, основанный на методологии дисконтирования денежных потоков. Если вы хотите вложить деньги в перспективный бизнес-проект, то неплохо было бы для начала рассчитать NPV этого проекта. Алгоритм расчета такой:

1. нужно оценить денежные потоки от проекта — первоначальное вложение (отток) денежных средств и ожидаемые поступления (притоки) денежных средств в будущем;
2. определить стоимость капитала (англ. Cost of Capital) для вас — это будет ставкой дисконтирования;
3. продисконтировать все денежные потоки (притоки и оттоки) от проекта по ставке, которую вы оценили в п.2);
4. Сложить. Сумма всех дисконтированных потоков и будет равна NPV проекта.

Если NPV больше нуля, то проект можно принять, если NPV меньше нуля, то проект стоит отвергнуть.

Логическое обоснование метода NPV очень простое. Если NPV равно нулю, это означает, что денежные потоки от проекта достаточны, чтобы:

• возместить инвестированный капитал и
• обеспечить необходимый доход на этот капитал.

Если NPV положительный, значит, проект принесет прибыль, и чем больше величина NPV, тем прибыльнее является данный проект для инвестора. Поскольку доход кредиторов (у кого вы брали деньги в долг) фиксирован, весь доход выше этого уровня принадлежит акционерам. Если компания одобрит проект с нулевым NPV, позиция акционеров останется неизменной – компания станет больше, но цена акции не вырастет. Однако, если проект имеет положительную NPV, акционеры станут богаче.

Расчет NPV. Пример

Формула расчета NPV выглядит сложно на взгляд человека, не относящего себя к математикам: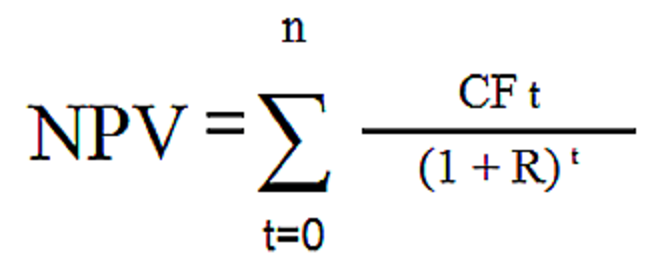
где

• n, t — количество временных периодов;
• CF — денежный поток (англ. Cash Flow);
• R — стоимость капитала, она же ставка дисконтирования (англ. Rate).

На самом деле эта формула — всего лишь правильное математическое представление суммирования нескольких величин. Чтобы рассчитать NPV, возьмем для примера два проекта A и B, которые имеют следующую структуру денежных потоков на ближайшие 4 года:

Таблица 1. Денежный поток проектов A и B.

Год	Проект A	Проект B
0	($10,000)	($10,000)
1	$5,000	$1,000
2	$4,000	$3,000
3	$3,000	$4,000
4	$1,000	$6,000

Оба проекта A и B имеют одинаковые первоначальные инвестиции в $10,000, но денежные потоки в последующие годы сильно разнятся. Проект A предполагает более быструю отдачу от инвестиций, но к четвертому году денежные поступления от проекта сильно упадут. Проект B, напротив, в первые два года показывает более низкие денежные притоки, чем поступления от Проекта A, но зато в последующие два года Проект B принесет больше денежных средств, чем проект A. Рассчитаем NPV инвестиционного проекта.

Для упрощения расчета предположим:

• все денежные потоки случаются в конце каждого года;
• первоначальный денежный отток (вложение денег) произошел в момент времени «ноль», т.е. сейчас;
• стоимость капитала (ставка дисконтирования) составляет 10%.

Напомним, что для того, чтобы привести денежный поток к сегодняшнему дню, нужно умножить денежную сумму на коэффициент 1/(1+R), при этом (1+R) надо возвести в степень, равную количеству лет. Величина этой дроби называется фактором или коэффициентом дисконтирования. Чтобы не вычислять каждый раз этот коэффициент, его можно посмотреть в специальной таблице, которая называется «таблица коэффициентов дисконтирования».

Применим формулу NPV для Проекта A. У нас четыре годовых периода и пять денежных потоков. Первый поток ($10,000) — это наша инвестиция в момент времени «ноль», то есть сегодня. Если развернуть формулу NPV, приведенную чуть выше, то мы получим сумму из пяти слагаемых:

Если подставить в эту сумму данные из таблицы для Проекта A вместо CF и ставку 10% вместо R, то получим следующее выражение:

То, что стоит в делителе, можно рассчитать, но проще взять готовое значение из таблицы коэффициентов дисконтирования и умножить эти коэффициенты на сумму денежного потока. В результате приведенная стоимость денежных потоков для проекта A равна $788,2. Расчет NPV для проекта A можно так же представить в виде таблицы и в виде шкалы времени:

Таблиц 2. Расчет NPV для проекта A.

Год	Проект A	Ставка 10%	Фактор	Сумма
0	($10,000)	1	1	($10,000)
1	$5,000	1 / (1.10) 1	0.9091	$4,545.5
2	$4,000	1 / (1.10) 2	0.8264	$3,305.8
3	$3,000	1 / (1.10) 3	0.7513	$2,253.9
4	$1,000	1 / (1.10) 4	0.6830	$683.0
ИТОГО:	$3,000	$788.2

Рисунок 1. Расчет NPV для проекта А.

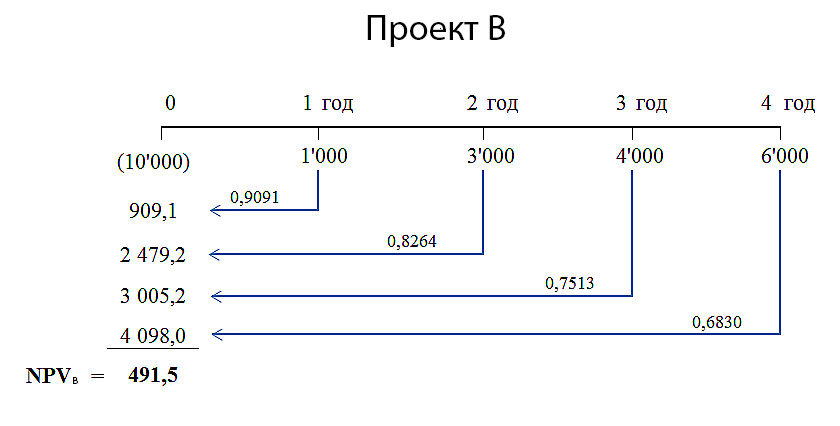
Аналогичным образом рассчитаем NPV для проекта B.

Поскольку коэффициенты дисконтирования уменьшаются с течением времени, вклад в приведенную стоимость проекта больших ($4,000 и $6,000), но отдалённых по времени (годы 3 и 4) денежных потоков будет меньше, чем вклад от денежных поступлений в первые годы проекта. Поэтому ожидаемо, что для проекта B чистая приведенная стоимость денежных потоков будет меньше, чем для проекта A. Наши расчеты NPV для проекта B дали результат — $491,5. Детальный расчет NPV для проекта B показан ниже.

Таблиц 2. Расчет NPV для проекта A.

Год	Проект B	Ставка 10%	Фактор	Сумма
0	($10,000)	1	1	($10,000)
1	$1,000	1 / (1.10) 1	0.9091	$909.1
2	$3,000	1 / (1.10) 2	0.8264	$2,479.2
3	$4,000	1 / (1.10) 3	0.7513	$3,005.2
4	$6,000	1 / (1.10) 4	0.6830	$4,098.0
ИТОГО:	$4,000	$491.5

Рисунок 2. Расчет NPV для проекта B.

Вывод

Оба эти проекта можно принять, так как NPV обоих проектов больше нуля, а, значит осуществление этих проектов приведет к увеличению доходов компании-инвестора. Если эти проекты взаимоисключающие и необходимо выбрать только один из них, то предпочтительнее выглядит проект A, поскольку его NPV=$788,2, что больше NPV=$491,5 проекта B.

Тонкости расчета NPV

Применить математическую формулу несложно, если известны все переменные. Когда у вас есть все цифры — денежные потоки и стоимость капитала, то вы легко сможете подставить их в формулу и рассчитать NPV. Но на практике не всё так просто. Реальная жизнь отличается от чистой математики тем, что невозможно точно определить величину переменных, которые входят в эту формулу. Собственно говоря, именно поэтому на практике примеров неудачных инвестиционных решений гораздо больше, чем удачных.

Денежные потоки

Самый важный и самый трудный шаг в анализе инвестиционных проектов — это оценка всех денежных потоков, связанных с проектом. Во-первых, это величина первоначальной инвестиции (оттока средств) сегодня. Во-вторых, это величины годовых притоков и оттоков денежных средств, которые ожидаются в последующие периоды.

Сделать точный прогноз всех расходов и доходов, связанных с большим комплексным проектом, невероятно трудно. Например, если инвестиционный проект связан с выпуском на рынок нового товара, то для расчета NPV необходимо будет сделать прогноз будущих продаж товара в штуках, и оценить цену продажи за единицу товара. Эти прогнозы основываются на оценке общего состояния экономики, эластичности спроса (зависимости уровня спроса от цены товара), потенциального эффекта от рекламы, предпочтений потребителей, а также реакции конкурентов на выход нового продукта.

Кроме того, необходимо будет сделать прогноз операционных расходов (платежей), а для этого оценить будущие цены на сырье, зарплату работников, коммунальные услуги, изменения ставок аренды, тенденции в изменении курсов валют, если какое-то сырье можно приобрести только за границей и так далее. И все эти оценки нужно сделать на несколько лет вперед.

Ставка дисконтирования

Ставка дисконтирования в формуле расчета NPV — это стоимость капитала для инвестора. Другими словами, это ставка процента, по которой компания-инвестор может привлечь финансовые ресурсы. В общем случае компания может получить финансирование из трех источников:

• взять в долг (обычно у банка);
• продать свои акции;
• использовать внутренние ресурсы (например, нераспределенную прибыль).

Финансовые ресурсы, которые могут быть получены из этих трех источников, имеют свою стоимость. И она разная! Наиболее понятна стоимость долговых обязательств. Это либо процент по долгосрочным кредитам, который требуют банки, либо процент по долгосрочным облигациям, если компания может выпустить свои долговые инструменты на финансовом рынке. Оценить стоимость финансирования из двух остальных источников сложнее. Финансистами давно разработаны несколько моделей для такой оценки, среди них небезызвестный CAPM (Capital Asset Pricing Model). Но есть и другие подходы.

Стоимость капитала для компании (и, следовательно, ставка дисконтирования в формуле NPV) будет средневзвешенная величина процентных ставок их этих трех источников. В англоязычной финансовой литературе это обозначается как WACC (Weighted Average Cost of Capital), что переводится как средневзвешенная стоимость капитала.

Зависимость NPV проекта от ставки дисконтирования

Понятно, что получить абсолютно точные величины всех денежных потоков проекта и точно определить стоимость капитала, т.е. ставку дисконтирования невозможно. В этой связи интересно проанализировать зависимость NPV от этих величин. У каждого проекта она будет разная. Наиболее часто делается анализ чувствительности показателя NPV от стоимости капитала. Давайте рассчитаем NPV по проектам A и B для разных ставок дисконтирования:

Стоимость капитала, %	NPV A	NPV B
0	$3,000	$4,000
2	$2,497.4	$3,176.3
4	$2,027.7	$2,420.0
6	$1,587.9	$1,724.4
8	$1,175.5	$1,083.5
10	$788.2	$491.5
12	$423.9	($55.3)
14	$80.8	($562.0)
16	($242.7)	($1,032.1)
18	($548.3)	($1,468.7)

Таблица 3. Зависимость NPV от ставки дисконтирования.

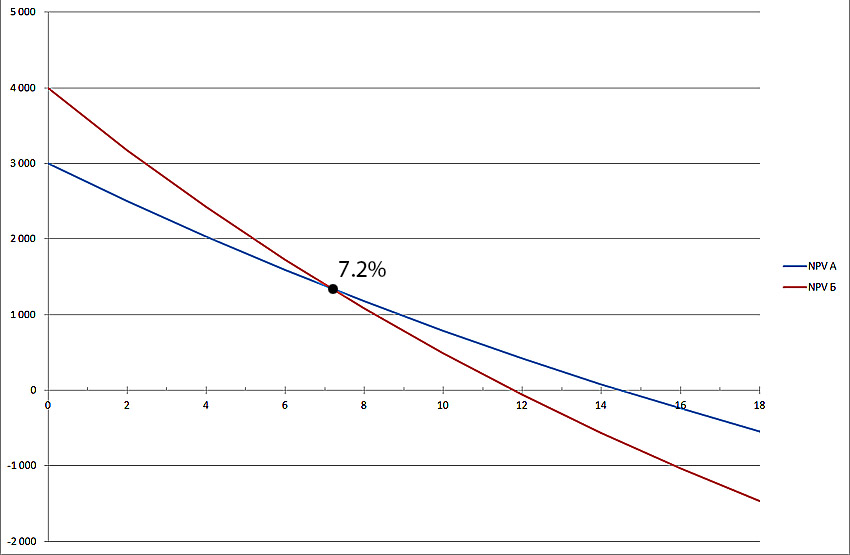
Табличная форма уступает графической по информативности, поэтому гораздо интереснее посмотреть результаты на графике (нажать, чтобы увеличить изображение):

Рисунок 3. Зависимость NPV от ставки дисконтирования.

Из графика видно, что NPV проекта A превышает NPV проекта B при ставке дисконтирования более 7% (точнее 7,2%). Это означает, что ошибка в оценке стоимости капитала для компании-инвестора может привести к ошибочному решению в плане того, какой проект из двух следует выбрать.

Кроме того, из графика также видно, что проект B является более чувствительным в отношении ставки дисконтирования. То есть NPV проекта B уменьшается быстрее по мере роста этой ставки. И это легко объяснимо. В проекте B денежные поступления в первые годы проекта невелики, со временем они увеличиваются. Но коэффициенты дисконтирования для более отдаленных периодов времени уменьшаются очень значительно. Поэтому вклад больших денежных потоков в чистую приведенную стоимость так же резко падает.

Например, можно рассчитать, чему будут равны $10,000 через 1 год, 4 года и 10 лет при ставках дисконтирования 5% и 10%, то наглядно можно увидеть, как сильно зависит приведенная стоимость денежного потока от времени его возникновения.

Таблица 4. Зависимость NPV от времени его возникновения.

Год	Ставка 5%	Ставка 10%	Разница, $	Разница, %
1	$9,524	$9,091	$433	4.5%
4	$8,227	$6,830	$1,397	17.0%
10	$6,139	$3,855	$2,284	37.2%

В последнем столбце таблицы видно, что один и тот же денежный поток ($10,000) при разных ставках дисконтирования отличается через год всего на 4.5%. Тогда как тот же самый по величине денежный поток, только через 10 лет от сегодняшнего дня при дисконтировании по ставке 10% будет на 37.2% меньше, чем его же приведенная стоимость при ставке дисконтирования 5%. Высокая стоимость капитала «съедает» существенную часть дохода от инвестиционного проекта в отдаленные годовые периоды, и с этим ничего не поделать.

Именно поэтому, при оценке инвестиционных проектов денежные потоки, отстоящие от сегодняшнего дня более, чем на 10 лет, обычно не используются. Помимо существенного влияния дисконтирования, еще и точность оценки отдаленных по времени денежных потоков существенно ниже.

Источник