Определение будущей стоимости сегодняшних инвестиций

Routes to finance

7 Расчет окупаемости в коммерческой недвижимости (Июнь 2021).

Инвестиции могут быть разнесены с течением времени — например, ежемесячное дополнение к вашему 401K, или, может быть, единовременная сумма инвестиций, например, покупка аннуитета. В последнем случае вы можете рассчитать будущую стоимость своих инвестиций, используя известную финансовую формулу, называемую «будущая стоимость единовременных инвестиций». Ниже приведены три разных способа решения проблемы. Каждый метод использует различные способы расчета, но базовая формула одинакова во всех трех случаях.

Проблема и формула будущей стоимости

Предположим, что у нас есть 100 долларов, а процентная ставка составляет 5%. Какова будет стоимость инвестиций в конце первого года? Формула для будущей стоимости этих инвестиций в единовременную сумму выглядит следующим образом:

FV ₁ = PV + INT или PV (1 + I) ⁿ

Первая часть этого уравнения — FV₁ = PV + INT — гласит: «будущее значение ( FV ) в конце одного года — нижний индекс ᵢ — равен текущей стоимости плюс добавленная стоимость по указанной процентной ставке.

Следующая формула представляет это в форме, которую легче вычислить добавленная сумма накопленного интереса — PV (1 + I) ⁿ — , которая гласит: «текущее значение ( PV) раз (1 + I) ⁿ , где l представляет процентную ставку, а верхний индекс ⁿ — это количество периодов рецептуры.

Теперь давайте рассмотрим пример сверху. В течение одного года ваши единовременные инвестиции в размере $ 100, составляющие 5% в год, будут равны:

FV = $ 100 (1 + 0. 05) = $ 105

В этом случае вы не видите надстрочный индекс (n) для так как на данный момент вы решаете только на первый год.

Если вы хотите определить значение в конце двух лет, ваш расчет будет выглядеть следующим образом:

FV = $ 100 (1 + 0. 05) ² = $ 110. 25

Вы можете решить эту проблему, которая представляет собой сложную задачу, путем вычисления значения в конце первого года, а затем умножения результата на ту же 5-процентную ставку на второй год:

FV = [$ 100 (1 + 0. 05)] + [$ 105 (1 + 0. 05)] = $ 110. 25

Вы можете продолжить этот процесс, чтобы найти будущую стоимость инвестиций для любого количества периодов рецептуры.

Описывая этот процесс — вручную добавляя добавленную стоимость каждого года из интереса, а затем используя это значение для проведения аналогичных вычислений для каждого следующего года — дает понять, как мы достигаем результата, но это отнимает много времени , Решение о будущем значении 20 лет в будущем означает повторение математики 20 раз. Есть более быстрые и лучшие способы решения этой проблемы, одним из которых является использование финансового калькулятора.

Будущая стоимость инвестиций с использованием финансового калькулятора

Формула для определения будущей стоимости инвестиций в финансовый калькулятор:

Хотя это не совсем так, это та же самая формула, которую мы использовали, когда мы вручную делали расчеты.

Кстати, вы можете использовать эту формулу с любым калькулятором, который имеет экспоненциальный функциональный ключ — большинство из них. Однако использовать финансовый калькулятор лучше, потому что он имеет выделенные ключи, соответствующие каждой из четырех переменных, которые мы будем использовать, ускоряя процесс и минимизируя возможность ошибки. Вот клавиши, которые вы будете пробивать:

Punch N и 2 (в течение 2 лет)

Punch I / YR и 5 (для процентной ставки 5%)

Punch PV и -105 (за сумму, которую мы рассчитываем на проценты в год 2)

Punch PMT и PMT (нет платежей за пределами первого)

Punch FV , который возвращает ответ в $ 110. 25

Преимущество финансового калькулятора над ручным методом очевидно. С калькулятором, это не сложнее или трудоемко решить для будущей стоимости через 20 лет, чем решить в течение одного года. Другой метод экономии времени использует электронную таблицу.

Будущая стоимость инвестиций в суммарную сумму с использованием таблицы

Таблицы, такие как Microsoft Excel, хорошо подходят для расчета временной стоимости денежных проблем. Функция, которую мы используем для будущей стоимости инвестиции или единовременной суммы в электронной таблице Excel:

Чтобы использовать функцию на листе , нажмите «Формулы» в строке заголовка, затем нажмите «Финансовый». Затем вы увидите список функций. Нажмите FV. Это откроет окно построителя формул, в котором вы увидите пять полей с надписью rate, nper, pmt, pv и . Если вы хотите определить будущую стоимость в конце двух лет, заполните поля следующим образом:

ставка (процентная ставка) =. 05

nper (общее количество периодов оплаты = 2

pmt (повторные платежи, в этом случае нет) = 0

pv (текущее значение, выраженное как отрицательное число) = -100

type ( это относится к срокам последующих платежей) = Поскольку их нет, введите 0

Более ранние версии Excel требуют, чтобы вы щелкнули по Рассчитать , чтобы увидеть результат . результат автоматически.

Источник

Будущая стоимость

Будущая стоимость — это стоимость в будущем инвестированных сейчас денежных средств.

Для определения будущей стоимости денежных потоков при ежегодном начислении применяется следующая формула: FV = PV (1+ r) n (1)

где, FV — будущая стоимость инвестиции через n лет; PV — стоимость инвестиции в начале периода; r — ставка процента в виде десятичной дроби (например 10% = 0,1); n — число лет в расчетном периоде.

Али одолжил у Рахима 3000 у.е.

Используя формулу (1) получим:

FV = 3000 (1+0,1)6 =3000 х 1,16 = 5314,80 у.е.

FV = 3000 (1+0,1)7 = 3000 х 1,17 =5846,10 у.е.

Используя таблицу С — 3 — будущая стоимость 1 у.е. за период, получим аналогичные результаты:

FV = 3000 х 1,7716 = 5314,80 у.е.

FV = 3000 х 1,9487 = 5846,10 у.е.

Будущая стоимость при начислении несколько раз в году определяется по следующей формуле:

FV = PV (1+ r/m)m* n (2)

где, FV, PV, r, n — аналогично, что в формуле (1), а m — количество начисления в год. Пример 4.

У Саида 4000 у.е.. Подходят к нему Маъруф, Санам и Ситора, чтобы одолжить у него эти деньги на три года по 12% годовых с начислениями соответственно каждые полгода, ежеквартально и ежемесячно.

Кому одолжит деньги Саид?

Естественно Саид одолжит деньги тому, от кого получит больше прибыли. Используя формулу (2) получим:

Маъруф вернет Саиду через три года:

FV = 4000 (1+0,12/2)2х3 = 4000х1,066 = 40 00х1,4185 = 5674 у.е. Санам вернет Саиду через три годы

FV = 4000(1+0,12/4)4х3 = 4000х1,0312 = 4000х1,4285=5703,20 у.е. Ситора вернет Саиду через три года

FV = 4000(1+0,01)12х3 = 4000х1,0136 = 4000х1,4307= 5722,80 у.е.

Дисконтированная стоимость будущего денежного потока называется текущей стоимостью денежных потоков.

Текущая стоимость будущих денежных поступлений вычисляется по формуле:

Текущая стоимость 1 у.е. для различных периодов и по разным процентным ставкам приведена в таблице С-1.

Рахим хочет через 5 лет за 10000 у.е. купить автомобиль. Процентная ставка 15%. Какую сумму должен иметь Рахим в настоящее время, чтобы через 5 лет купить автомобиль. Используя формулу (3) получим: PV = 10000/(1+0,15)5=10000/1,15=4972 у.е.

То же самое получим, используя таблицу С-1 PV= 10000х0,4972=4972 у.е.

Источник

Определение будущей стоимости сегодняшних инвестиций

Будущая стоимость инвестиций – это сумма, до которой возрастет первоначальный вклад с учетом капитализации на основе сложных процентов, в течение периода хранения средств на счете.

Расчет будущей стоимости инвестиций осуществляется с использованием стандартных формул.

Чтобы их усвоить, достаточно попрактиковаться на простом примере.

Допустим, у нас имеется вклад в размере 1000 долл. под 7% годовых. Будущая стоимость инвестиций в данном случае может быть рассчитана по следующей формуле:

Будущая стоимость на конец 1-го периода = 1000 долл. * (1 + 0,07) = 1070 долл.

В случае продления срока действия вклада на тех же условиях еще на год будущую стоимость вклада следует рассчитывать по той же формуле с учетом полученного результата:

Будущая стоимость на конец 2-го периода = 1070 долл. * (1 + 0,07) = 1144,9 долл.

Понятно, что этот процесс может быть продолжен сколь угодно долго.

Формула расчета будущей стоимости инвестиций

Было бы удобно, не производя промежуточных расчетов, сразу получать значения будущей стоимости денег (инвестиций) на некоторый период времени, располагая данными о [1] размере первоначального вклада и [2] размере процентной ставки.

Для этого выведем общую формулу.

Для сокращения записи обозначим будущую стоимость инвестиций на конец n-го периода буквой S_n, размер первоначального вклада – буквой N, размер процентной ставки – k.

Тогда наша формула примет вид:

В частности, будущая стоимость инвестиций на конец 2-го периода с учетом наших первоначальных данных будет рассчитана по формуле 1000 долл. * (1+7/100) 2 = 1000 долл. * 1,1449 = 1144,9 долл., что соответствует полученному нами ранее результату.

Таблица расчета будущей стоимости инвестиций

На практике производить вручную приведенные выше расчеты бывает крайне утомительным.

Рассчитать будущую стоимость инвестиций на конец хотя бы 10-го периода способны разве что истинные фанаты счетного дела.

Попробуйте, к примеру, возвести в 10-ю степень число 1,07; лично я сразу начинаю искать калькулятор или что-то в этом роде…

До изобретения калькуляторов и компьютеров широко использовались таблицы с уже готовыми результатами.

На практике такие таблицы могут оказаться очень удобными в использовании.

Чтобы было понятно, о чем идет речь, предлагаю взглянуть на таблицу ниже:

Таблица содержит коэффициенты для 1 долл. (значения коэффициентов округлены до 3-го знака после запятой).

В частности, по истечению 2-го периода (года) при 7-процентной ставке размер вклада составит 1,145 долл. Если первоначальная сумма вклада составляла 1000 долл., то для расчета будущей стоимости вклада нужно его первоначальный размер умножить на соответствующий коэффициент из таблицы (1000 долл. * 1,145 = 1145 долл.).

Будущая стоимость инвестиций: важные закономерности

Внимательно присмотревшись к таблице, можно сделать несколько основополагающих выводов относительно формирования будущей стоимости инвестиций.

Во-первых, чем выше процентная ставка по вкладу, тем выше размер будущей стоимости.

Во-вторых, для каждой процентной ставки характерно увеличение размера будущей стоимости инвестиций с течением времени.

Наконец, в-третьих, коэффициент наращения будущей стоимости, как правило, всегда больше 1; он может быть равен 1 лишь в случае, когда процентная ставка равна 0.

В таком случае будущая стоимость инвестиций оказывается равной первоначальному вкладу, что случается, например, когда, вы просто одалживаете деньги на некоторый срок своим знакомым без взимания процентов за пользование одолженными средствами.

Конечно, использование таблиц не лишено недостатков.

Их расширение может представлять определенные трудности.

Если нам понадобится узнать размер капитала через 100 периодов, потребуется довольно обширная таблица, пользование которой окажется не таким уж простым делом.

На сегодняшний момент оптимальным следует признать использование так называемых инвестиционных калькуляторов, позволяющих в режиме онлайн производить соответствующие расчеты и мгновенно получать интересующие нас результаты.

Резюме

Сегодняшняя статья не охватывает всех аспектов, касающихся описания концепции сложных процентов и концепции будущей стоимости, а также связанных с этими концепциями расчетов.

Существует ряд формул, позволяющих рассчитывать будущую стоимость аннуитета (потока равных сумм денежных средств), приведенной стоимости, которые будет полезно усвоить каждому вдумчивому инвестору.

Но обо всем об этом мы поговорим в другой раз. Так что до скорой встречи и удачных инвестиций!

Источник

Будущая стоимость инвестиций

Для расчета будущих величин используется формула сложных процентов:

где FV – (англ. future value ) – будущая величина той суммы, которую мы инвестируем в любой форме сегодня .; PV – ( англ. present value ) – текущая (современная) стоимость той суммы, которую мы инвестируем ради получения дохода в будущем; k – доходность инвестиций; n – число периодов времени, в течении которых наши инвестиции будут участвовать в коммерческом обороте.

Значение множителя (1+k) можно взять в приложении табл.1.

Финансовые операции, предполагающие ежегодный денежный взнос с целью накопления определенной суммы в будущем, называются аннуитетом (англ. annuity – ежегодный платеж). Окончательная сумма аннуитета определяется по формуле:

FVA_n = PMT_t * (1+k) n-t ; (1.2)

где FVA_n – будущая стоимость аннуитета_, PMT_t — платеж, осуществляемый в конце периода t; k – уровень дохода; n – число периодов получения дохода.

Если сумма платежей одинакова в каждом периоде, формула 1.2 принимает вид:

где РМТ – годовая сумма денежного потока; FVA1_n;k – будущая стоимость аннуитета 1 рубля в конце каждого периода.

Значение этого показателя (FVA1n;k) можно взять из приложения (прил.3).

Пример 1. Вы решили сформировать личный фонд путем откладывания в конце каждого из 30 лет вашей трудовой деятельности по 1000 тыс. руб. на банковский счет со ставкой 10% годовых. Спрашивается сколько средств будет на вашем счете через 30 лет?

FVA₃₀ = PMT FVA1_20;10 = 1000*164,49 = 164490 (руб.)

Может быть обратная задача.

Пример 2. Алюминиевому заводу предстоит через 5 лет заменить установку в 100 тыс. руб. Есть договоренность с банком об открытии накопительного счета со ставкой 10% годовых. Сколько предприятию надо ежегодно перечислять на этот счет?

PMT = FVA₅/FVA1_5;10 (из формулы 1.3)

FVA1_5;10 = 6,105 (см приложение табл. 2) , тогда РМТ = 100 / 6,105 = 16,380 тыс. руб.

Предоставляя долгосрочные кредиты, зачастую банки используют изменяющиеся во времени, но заранее фиксированные для каждого периода процентные ставки. В этом случае наращенная сумма может быть определена по формуле:

FV=PV (1+ k ₁) n 1 (1+ k ₂) n 2 х(1+ k ₃) n 3 х…х(1+ k ₁₂) nk ; (1.5)

Где S – наращенная сумма; P – сумма капитала, предоставляемого в кредит; k ₁ , k ₂… k ₁₂ – последовательные значения ставок процентов; n₁, n₂ …n_k — периоды, в течении которых используются соответствующие ставки.

В случае, когда срок финансовой сделки выражен дробным числом, начисление процентов может выполняться по формуле сложных процентов:

FV=PV (1+ k) a + b ; (1.6)

где n=a+b – период сделки; а – целое число лет; b – дробная часть года.

Если в контракте на получение кредита предусматривается капитализация процентов несколько раз в году (по полугодиям, кварталам, помесячно), тогда для определения наращенной суммы применяется следующая формула:

FV=PV (1+ j /m) N ; (1.7)

где j – номинальная годовая процентная ставка; m – число периодов начисления процентов; N – число периодов начисления процентов за весь срок контракта; N=m*n, где n – число лет.

Пример 3. Получен кредит в размере 150 тыс. руб. сроком на два года, под 15% годовых. Начисление процентов производится ежеквартально. Определить наращенную сумму, подлежащую возврату.

FV =150(1+0,15/4) 2*4 =150*1,3425=201,37 (тыс. руб.)

Если срок ссуды измеряется дробным числом лет, а начисление процентов производится m раз в году, то наращенная сумма может быть определена по общей формуле, используемой при начислении сложных процентов, или по смешанному методу. В последнем случае наращенная сумма определяется по формуле:

FV=PV (1+j/m) ml (1+a j / m ); (1.8)

где ml – число полных периодов начисления процентов; а – дробная часть периода начисления процентов.

Текущая стоимость денег

Нахождение текущей (современной) величины денежных потоков на некоторый момент времени производится с помощью дисконтирования. С помощью дисконтирования в финансовых вычислениях учитывается фактор времени. Суть этого метода в следующем:

нахождение текущей величины PV(P) на некоторый момент времени при условии, что в будущем при начислении на неё процентов она могла бы составить наращенную сумму FV(S).

При дисконтировании решается задача, обратная определению наращенной суммы. Она формулируется следующим образом:

Какую сумму необходимо инвестировать (положить в банк) на n лет, чтобы при определённой доходности инвестиций (ставке процентов) i получит наращенную сумму, равную S. Для решения этой задачи используется формула 1.1:

PV=FV/(1+k) n или PV= FV (1+k) — n (2.1)

где (1+n) — n – дисконтный множитель, показывающий во сколько раз первоначальная сумма меньше наращенной (прил.2).

Пример 4. Через 1 год владелец векселя, выданного коммерческим банком, должен получить по нему 10 тыс. руб. Какая сумма была внесена в банк в момент приобретения векселя, если доходность векселя должна составлять 25% годовых? По формуле (2.1) получим:

PV=10 / (1+0,25) 1 =8,0 тыс. руб.

ТЕМА 2. АНАЛИЗ ФИНАНСОВЫХ ИНВЕСТИЦИЙ

Анализ доходности облигаций

Текущий годовой доход по облигации определяется по формуле:

, ( 2.4 )

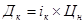
где Д_к — сумма купонных выплат;

i_K — купонная годовая процентная ставка (норма доходности);

Ц_н — номинальная цена облигации.

Купонный доход облигации определяется по формуле точных процентов:.

, ( 2.5 )

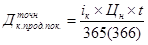
где 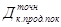— купонный доход продавца, покупателя;

I_r – годовой купонный доход, %;

t — для продавца – количество дней владения облигаций; для покупателя – число дней от даты продажи до очередного «процентного дня»;

Годовая ставка дополнительного дохода (убытка) облигации ( iDD) определяется по формуле:

, ( 2.6 )

где — • величина дополнительного дохода (убытка)

( 2.7 )

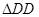
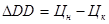
Ставка помещения капитала (совокупного дохода за год — ICD) определяется по формуле:

( 2.8 )

, ( 2.9 )

где i_k. — ставка купонного дохода;

iDD — годовая ставка дополнительного дохода (убытка) облигации (формула ).

Ставка совокупного дохода по облигации за весь срок займа (iCD3)

ICD3= 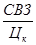( 2.10 )

ICD3 = . ( 2.11 )

Совокупный годовой доход по облигации (CDгод) определяется по формуле:

; ( 2.12 )

Совокупный годовой доход по облигации за весь срок займа (CD3) определяется по формуле:

; ( 2.13 )

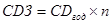
Анализ доходности акций

Курс акции рассчитывается по формуле:

где К_а – курс акции; Ц_р – рыночная цена; Ц_н – номинальная цена.

Текущая доходность инвестированных средств (R — рендит акции) определяется по формуле:

( 2.15 )

где D_д — дивидендный доход; Цпр — цена приобретения (эмиссионная или рыночная).

Источник