Доходность на фондовом рынке
Тот, кто уже провел некоторое время на фондовом рынке, знает, что его доходность может описываться по разному. Бывает доходность среднеарифметическая и среднегеометрическая (учитывающая сложный процент). Бывает без учета и с учетом реинвестирования дивидендов или купонов (полная доходность). Бывает за вычетом налогообложения дивидендов и без этого вычета. Бывает номинальная и реальная (за вычетом инфляции). Подробнее о видах доходности можно прочитать здесь.
Доходность рынка: понимайте правильно!
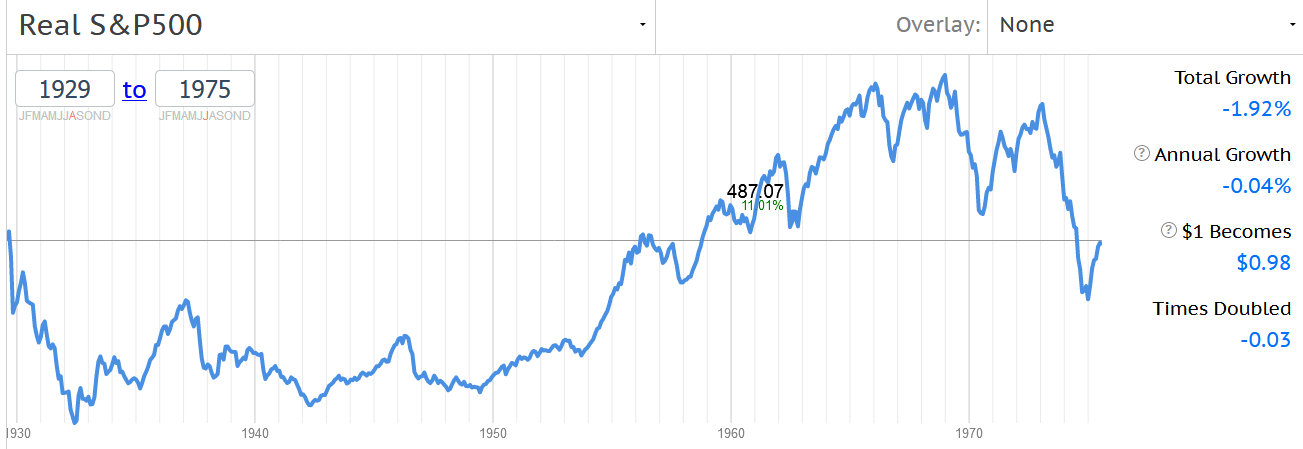
Понимать, что именно вы видите, очень важно, поскольку авторы могут трактовать различные виды графиков в пользу своих воззрений. К примеру, график инвестиций в рынок США с 1929 по 1975 год без учета дивидендов, но с учетом инфляции оказывается в нуле:
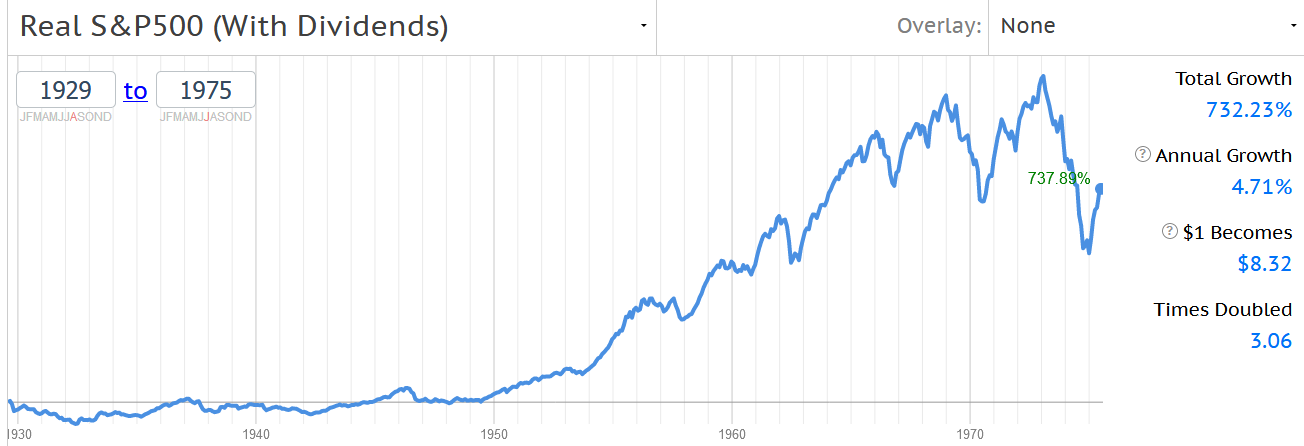
Из подобных картинок иногда делают вывод, что американский рынок вовсе не так эффективен на долгосроке, как об этом говорит множество других исследований. Однако с учетом дивидендов картина оказывается заметно лучше и дает уже 4.7% в год с общим ростом более, чем на 700%:
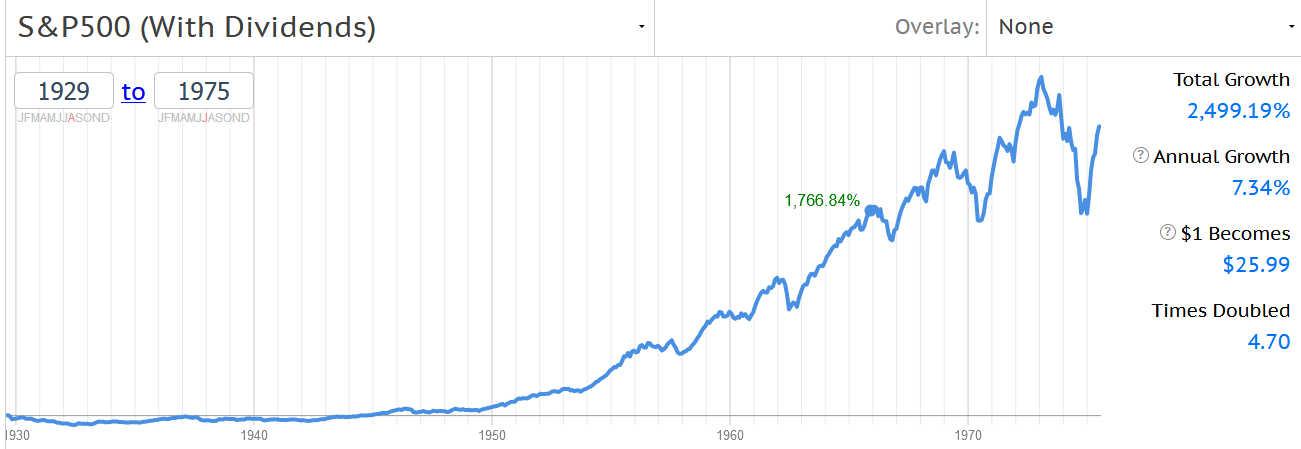
А если мы возьмем общую доходность рынка с дивидендами, но без учета инфляции, то и вовсе получим почти 7.5% годовых:
Какой из этих трех графиков «правильный»? Ответ: все. Вот только результат на них колеблется от нуля до почти 7.5% в год на отрезке в 45 лет. Есть смысл понимать, что вы получите реально — не правда ли?
Как возникает рыночная доходность?
Однако не меньше, а скорее заметно больше непонимания возникает по поводу того, как именно формируется рыночная доходность. Дело в том, что в ней участвует как спекулятивная, так и инвестиционная составляющая — тогда как внятно объяснить разницу между инвестициями и спекуляциями сумеет не так много людей.
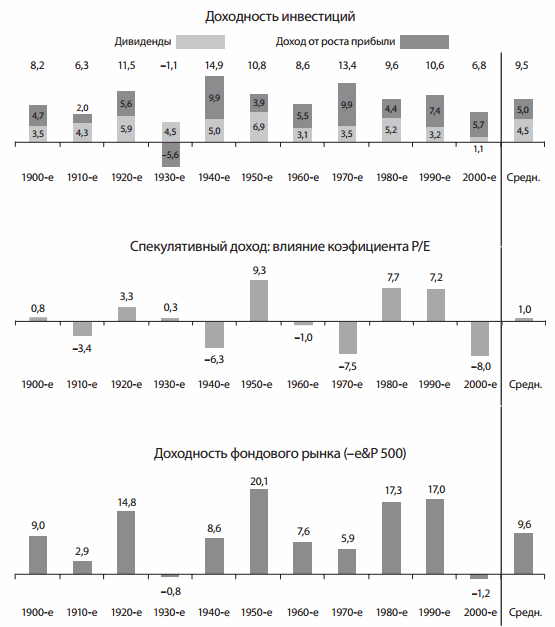
Но как известно, все уже украдено до нас. В книге Богла есть отличная иллюстрация, поясняющая этот вопрос:
Пояснения к картинке. В самом верху мы видим доходность американского бизнеса, т.е. то, сколько получили его собственники. Результаты из финансовой отчетности компаний. Только в 1930-е этот результат оказывается отрицательным, тогда как в остальные десятилетия значения положительны. Обратим также внимание на среднее значение в 9.5% годовых.
Теперь перейдем вниз. Тут мы видим доходность фондового рынка, т.е. акционеров всех компаний из биржевого индекса. По десятилетиям она несколько отличается от дохода собственников, однако среднее значение практически совпадает: акционеры получили 9.6% годовых.
Наконец, в середине диаграммы стоит влияние коэффициента цена/прибыль. Тут представлена разница между коэффициентом в определенное десятилетие и средним P/E на промежутке в 100 лет. Положительное значение означает спекулятивный рост (переоценку акций). Отрицательное значение говорит о депрессивном рынке. Однако средний показатель на длинной дистанции оказывается почти равен нулю.
Какой из этого вывод? Доходность собственников бизнеса на длинной дистанции равна доходу акционеров . Это и есть инвестиции — покупать акции или их фонды, получая процент от бизнеса компании. Влияние спекулянтов, пытающихся ловить ценовые колебания и «гоняющих рынок» вверх и вниз относительно доходности бизнеса, со временем сводится к нулю, хотя в пределах десятилетия или даже больше это влияние может быть весьма заметным.
Что происходило, например, в 1980-е и 1990-е годы? Вокруг акций США был повышенный ажиотаж, за них готовы были платить приличные деньги в расчете на рост прибыли. Когда находился один покупатель, за ним следовал другой, повышая спрос. Инвестор в акции в это время получил заметно больше собственников бизнеса (см. столбцы диаграммы).
Тем не менее нетрудно заметить, что акционеры не всегда в выигрыше: например, так было в 1970-е и 2000-е годы. В это время на рынках был депрессивный настрой и за акции платили мало, так что акционер получил меньше, чем владельцы бизнеса.
Формула рыночной доходности
Итак, рассматривая рынок акций, формула рыночной доходности для инвестора оказывается довольно простой. Доход на фондовом рынке складывается из двух составляющих:
Прибыль = дивиденды + рост котировок акций (доходность рынка)
Исторически за последние 100 лет эти составляющие на рынке США распределялись примерно поровну (5% в год на рост акций и 4.5% на дивиденды). Однако на более коротких отрезках их влияние на результат сильно различалось: в 1930-е годы дивиденды были главным доходом акционеров, а во второй половине 1990-х вся доходность получалась от бурного роста котировок акций технологического сектора, которые платили минимальные дивиденды или не платили их вовсе.
Как получить рыночную доходность?
Для инвестора полная рыночная доходность недостижима, хотя к ней можно близко приблизиться. Причиной являются рыночные посредники, без которых для частного инвестора инвестиции невозможны. Где теряет инвестор?
1. Комиссии брокеру . За проведение любой операции, в частности покупки и продажи актива, брокер берет от одного до нескольких долларов. Это гораздо меньше, чем десятилетия назад, и уже сегодня некоторые брокеры в США предлагают эту услугу бесплатно. Как уменьшить ее влияние? Минимизировать число сделок, в том числе не производя операций на малые суммы.
2. Комиссии управляющей компании . Приобретая диверсифицированные фонды ETF со множеством бумаг, мы должны платить комиссию за управление. Т.е. за то, чтобы фонд придерживался состава копируемого им индекса. Уменьшить влияние этой комиссии можно подбором фонда — в некоторых случаях сегодня они взимают менее 0.1% в год.
3. Налоговые отчисления . С прибыли нужно заплатить налог государству в 13%. При зарубежном инвестировании избежать его нельзя, но можно растянуть во времени — налог не платится, пока прибыль не зафиксирована. А значит, пока акция растет, но не продана, ее прибыль работает по правилу сложного процента. На российском брокерском счету можно избежать уплаты налога, открыв ИИС.
4. Комиссии за ввод и вывод средств . Банки и брокеры как правило берут комиссии за переводы, хотя у некоторых брокеров есть лимит на бесплатный вывод — скажем, раз в месяц. В результате
Прибыль инвестора = доходность рынка – издержки – налоги
Можно ли получить больше доходности рынка?
Разобравшись с этим вопросом, попробуем понять, как можно обыграть рынок. Т.е. получить доход выше рыночного. Для этого нужно угадывать движения рыночной кривой, т.е. спекулятивный настрой других участников. Отнимая у них деньги, в теории можно превзойти биржевой индекс.
Инвестор = получает результат от работы бизнеса
Спекулянт = получает результат от игроков рынка
Представим себе такую картинку. На фондовом рынке находятся только шесть человек, которые покупают и продают акции. Цель — получить доход выше рынка. Предположим, рыночная доходность составила 7% в год. Один участник получил 32%. Что это значит?
Значит, он обыграл рынок на 25%. Откуда возьмется эта «избыточная» доходность? Из результата других пяти участников. Если предположить, что у них будет одинаковый доход, то все пятеро окажутся на 5% хуже рынка. Соответственно, доходность каждого составит только 2% годовых. Если же по 30% заработают два участника, то остальные уйдут в минус.
Насколько реально быть в числе победителей? Основную роль на рынке задает крупный капитал, размещаемый профессиональными инвесторами. В результате вы сражаетесь против профессиональных бойцов, которые сами несут большие потери. Результат: за 10 лет рынок обгоняют не более 2-3 активно управляемых фондов из десяти. Читайте здесь.
Доходность разумного инвестора
Таким образом, не стоит пытаться обыграть рынок — но нужно стремится взять от него по максимуму. Почему? Потому что даже потери в 1% дохода это более 10% за десять лет. Следовательно, на доход в 100 000 можно недополучить более 10 000 долларов. Потери 2-3% в год на длинной дистанции могут стоить от трети до половины (!) дохода. Что делать? Для оптимального результата нужно составить грамотный инвестиционный портфель с учетом следующих факторов:
- Выбирайте брокера с минимальными комиссиями за сделку
- Старайтесь совершать как можно меньше сделок
- Используйте в портфеле ликвидные индексные фонды с минимальной комиссией за управление
- Учитывайте комиссию брокера за вывод средств — в некоторых случаях она может быть 30-50$
- Учитывайте комиссию за неактивность — иногда брокеры снимают деньги за месяц, в котором вы не совершали сделок
- Учитывайте налоги — продажа актива с прибылью влечет его уплату. В расчете на рост капитала также целесообразно использовать фонды, реинвестирующие дивиденды, чтобы не платить дивидендный налог
Источник
Расчет рыночной доходности
Формула расчета рыночной доходности
Любому, кто занимается вложением средств, необходимо уметь грамотно рассчитывать доходность — как для собственных нужд, так и для правильного прочтения различных источников, где указываются результаты инвестиций. В самом простом случае — банковского депозита — рост дохода происходит по прямой линии и сложных расчетов не требуется.
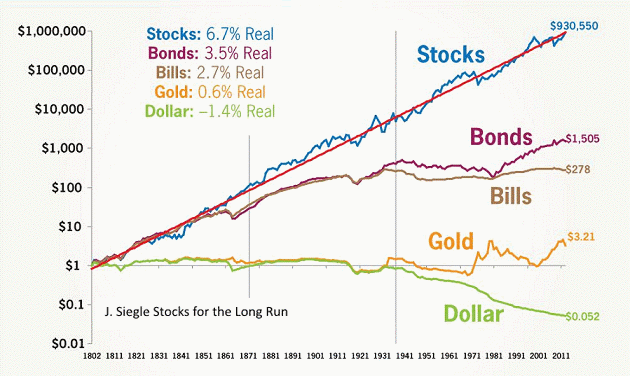
Однако если мы возьмем банковский депозит с возможностью капитализации процентов, то картина уже изменится: счет начнет расти по экспоненте. Аналогичный, но более сильный эффект дает инвестирование на фондовом рынке в акции (логарифмическая шкала):
Вообще говоря, в сети нетрудно найти калькулятор сложного процента — но подойдет он отнюдь не для каждой задачи и поскольку содержит формулу в закрытом виде, то не дает понимания о сути расчета. Непонимание работы с рыночными данными способно привести к ошибкам даже в самых простых случаях. Ниже мы рассмотрим, как посчитать доходность в процентах для разных случаев.
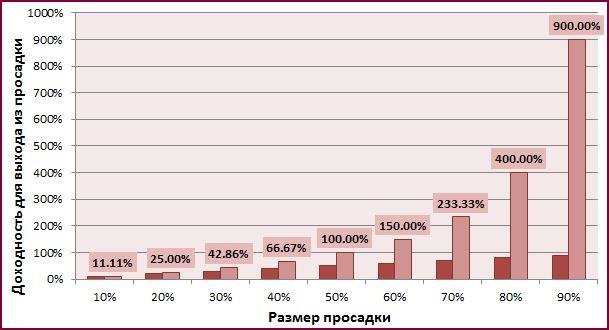
Из этого следует очень важное правило: чем выше просадка, тем большая доходность требуется, чтобы ее отыграть . К примеру, если стоимость актива за год уменьшилась на 80% (осталось только 20% начальной цены), то требуется доходность в целых 400%, чтобы достичь первоначального уровня:
Именно поэтому агрессивные стратегии с высоким кредитным плечом не живут долго — математическое ожидание даже при большей вероятности прибыли, чем убытка все равно со временем уничтожит депозит.
В общем случае формула доходности выглядит так:
A(n) = A(n-1) × (1 + X) = A(0) × (1 + X)^n или X = (A(2)/A(0))^(1/n) – 1
- A(0) – исходное количество денег
- А(n) – количество денег через n лет
- X – годовая доходность (в процентах)
Если же взять изменение за год в разах (Y) (т.е. мы рассматриваем изменение на 10% как рост в 1,1 раза, Y = 1 + 10/100 = 1,1), то
A(n) = A(n-1) × Y = A(0) × Y^n
Задача
Актив растет на 10% в год. Какова будет его доходность через 2 года?
Можно искать калькулятор сложного процента, а можно сказать, что Y = 1.1, число лет n = 2. Тогда взяв исходное количество денег за условную единицу
А(2) = 1 × 1.1² = 1.21, т.е. актив вырастет на 21% (из 1000 рублей будет 1210)
Обратная задача
Найти среднюю годовую доходность при росте актива на 21% в течение двух лет (понятно, что она может расти неравномерно — мы же найдем среднюю величину):
Снова принимая нашу первоначальную доходность за условную единицу, считаем:
Y = (1.21/1)½ = 1.1, т.е. усредненная доходность равна 10%
Задача 2
За четыре года банковский вклад с ежегодной капитализацией прибыли вырос от 100.000 рублей до 150.000 рублей. Какова средняя доходность в годовом исчислении?
Y = (150.000/100.000)^(1/4) = 1.10668, т.е. средняя годовая доходность равна 10.67%
Соответственно, просто разделив 50% на 4 мы получили бы среднеарифметическую доходность 12.5%, что неверно. Эта разница и есть преимущество сложного процента: без него доходность каждый год начислялась бы на 100.000 рублей — т.е. каждый год мы получали бы 12.500, что за четыре года и даст ровно 50.000. Однако при ежегодной капитализации мы добиваемся того же результата уже с меньшим процентом (10.67%).
Задача 3
За 2 года и 6 месяцев стоимость пая в инвестиционном фонде выросла на 42.7% (допустим, пай стоил 5 рублей, а стал стоить 7.135 рубля — значит, 7.135/5 = 1.427). Какова средняя доходность фонда в год?
2 года и 6 месяцев это 2.5 года (n = 2.5), а Y = 1.427. Тогда
Y = (1.427/1)^(1/2.5) = 1.1528, т.е. средняя годовая доходность равна 15.28%
Если за «n» обозначить количество месяцев (n = 30), то теперь можно вычислить и среднемесячную доходность (1.427^(1/30) = 1.0119 или 1.19%. При этом среднеарифметическая доходность была бы 42.7/30 = 1.4233%). Если мы возьмем банковский депозит, где капитализация происходит ежемесячно, то считать надо в месяцах, если ежегодно — то в годах.
Задача 4
Значение индекса ММВБ на конец декабря 1997 года – 85.05 пунктов. Значение индекса ММВБ на конец 2007 года – 1888.86 пунктов. Какова среднегодовая доходность индекса ММВБ за 10 лет?
Y = (A(2)/A(0))^(1/n) = (1888.86/85.05)^(1/10) = 1.3635 или 36.35%
Задача 5
Ниже дана российская инфляция за 2000-2007 годы. Нужно рассчитать среднегодовую.
2000 г. – 20,2%
2001 г. – 18,6%
2002 г. – 15,1%
2003 г. – 12,0%
2004 г. – 11,7%
2005 г. – 10,9%
2006 г. – 9,0%
2007 г. – 11,9%
Это как раз случай, хорошо приближенный к реальности — доходность фондового рынка можно смотреть как по разнице пунктов за выбранный промежуток времени, так и считать (или брать из справочника) по годам. Тогда общий рост потребительской корзины:
1,202 × 1,186 × 1,151 × 1,120 × 1,117 × 1,109 × 1,090 × 1,119 = 2,777 раза (или на 177%)
И средняя инфляция
Y = (A(2)/A(0))^(1/n) =2.777^(1/8) = 1.1362 или 13.62%
P.S. Задача аналогично может быть использована для расчета средней доходности активов, которая за год бывает отрицательной. В этом случае коэффициент берется меньше 1, например при доходности минус 10% в год он равен 1 — 10/100 = 0.9.
Задача 6
Инвестор входит в некоторый счет, который показывает в текущий момент 1500%. Выходит из него через полгода, когда показатель достигает 1700%. Пусть он инвестировал 500 долларов и получил 70% от роста котировок. Каков его доход в % годовых и по абсолютной величине?
Это не 200%, умноженные на 0.7! Считаем: (1 + 1700/100)/(1 + 1500/100) и получаем 1.125, т.е. 12.5% за полгода. Следовательно, среднеарифметически в год будет в два раза больше, а среднегеометрически 1.125^(1/0.5) = 26.56%. Хотя такой расчет в этом случае не будет корректен — мы экстраполируем прибыль, т.е. считаем не только имеющийся, но и будущий результат.
Как видно, в этом случае среднегеометрическая доходность получается выше среднеарифметической — так что таким приемом иногда пользуются инвестиционные фонды, экстраполируя удачные квартальные результаты на целый год. Если же нужно рассчитать доход на 500 долларов за время инвестирования, то сначала учтем, что инвестор получает лишь 70% от роста, т.е. 12.5% × 0.7 = 8.75%. Следовательно, прибыль равна 500 × 8.75% / 100% = 43.75 долларов.
Похожий пример: вошли в счет на отметке доходности в 30%, вышли на 90%. При этом прибыль инвестора увеличилась не в три раза, а на (1 + 90/100)/(1 + 30/100) ≈ 1.46, т.е. примерно на 46%. Если взять 500 долларов, инвестированные в счет, то суммарный баланс составит примерно 730 долларов (прибыль около 230 $).
Задача 7
Расчет доходности акций с учетом дивидендов и курсового роста стоимости. Пусть была куплена акция одной компании за 120 рублей. Спустя какое-то время по ней получены дивиденды 7.2 рубля, а котировки выросли до 135 рублей — после чего акцию продали. Рассчитать полученный доход.
Y = [(7.2 + (135-120))/120] × 100% = 18.5%
Задача 8
По данным предыдущего примера рассчитать доходность в процентах годовых, если на момент продажи акции (достижения ее стоимости 135 рублей) прошло 250 дней:
Y = [(7.2 + (135-120))/120] × 365/250 × 100% = 27.01%
Источник