Нормальном распределении логарифмической доходности

логарифмическая доходность

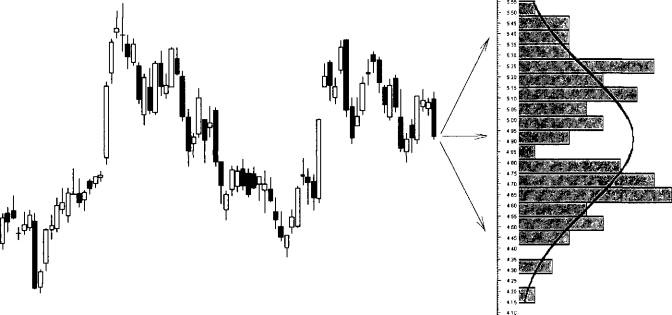
Для анализа также еще используют данные об изменении цен либо логарифмическую доходность — отношение логарифмов, обычно натуральных, цен изучаемого ряда. Мы не будем проникать в дебри статистического анализа, выясняя тип распределения на рисунке 1 — 1, поскольку этот вопрос слишком большой, и для нас он сейчас не слишком важен. Заметим, по-видимому, в данном случае мы имеем дело с распределением Парето либо Стьюдента, подклассом которого является нормальное распределение. В распространенных опционных моделях обычно основываются на логнормальном, или логарифмически-нормальном распределении: распределении случайной величины, логарифм которой характеризуется нормальным распределением. В связи с этим следует отметить, что предположение о нормальности или лог-нормальности распределения ценовых рядов достаточно условно: строгое использование гипотезы о нормальности распределения вовлечет в модель ценообразования отрицательные цены.

Фактически кривая распределения цен показывает нам вероятность достижения в будущем ценой интересующего нас значения. Математическое моделирование позволяет ввести различные предположения относительно формы распределения, а также продолжить «хвосты» в обе стороны, которые для рассматриваемого ценового ряда относятся к разряду стресс-ситуаций. Тем не менее, их обычно учитывают в моделях, вводя ограничения через параметр доверительного уровня, принимающего разные значения в зависимости от выдвигаемых предположений и методологии расчетов.

Очевидно: чем больше срок действия опциона, тем дальше от текущих значений могут сдвинуться цены, поэтому премия опциона растет с увеличением срока до истечения. Собственно, премия опциона определяется суммированием результатов всех исходов, взвешенных по вероятности, корректируемых по ставке, чтобы получить приведенную стоимость. Так как опцион — всего лишь одна из инвестиционных альтернатив, то приходится учитывать влияние арбитража, устраняющего рыночные диспропорции с помощью разнообразных, но связанных между собой финансовых инструментов. Все вычислительные расчеты, необходимые для определения опционной премии, которую иногда называют «справедливой», говоря о теоретических ценах, как раз и выполняют многочисленные модели ценообразования опционов.

Рис. 1-1. Дневной график цен РАО «ЕЭС России» (ММВБ) за четыре месяца, а также распределение цен

Следует отметить: в реальности определить, что такое «справедливая цена», — очень сложно, если вообще возможно. В принципе, это весьма эфемерная величина, поскольку некоторые параметры для модели берутся непосредственно из рынка, поэтому любые текущие цены являются по большому счету «справедливыми», вне зависимости от обстоятельств. Единственное, что можно предположить — это возможность ошибки рыночных игроков, переоценивших рынок в данный момент времени или недооценивших его.

Подводя итог, остается заметить: физический смысл опционной премии в том, что она показывает, сколько инвестор готов заплатить в текущий момент времени за право обладания рисковым активом. Собственно, эта задача, получившая название «Петербургский парадокс», известна более четверти тысячелетия и впервые была поставлена Бернулли, затем и решившим ее.

Статья размещена в рубрике: Риск менеджмент

Источник

Логнормальное распределение

Что такое Логнормальное распределение?

Логарифмическое нормальное распределение – это статистическое распределение логарифмических значений из соответствующего нормального распределения. Логарифмически нормальное распределение можно преобразовать в нормальное распределение и наоборот, используя соответствующие логарифмические вычисления.

Понимание нормального и логнормального

Нормальное распределение – это распределение вероятностей результатов, которое является симметричным или образующим кривую колокола. При нормальном распределении 68% результатов попадают в одно стандартное отклонение, а 95% – в два стандартных отклонения.

Хотя большинство людей знакомы с нормальным распределением, они могут быть не так знакомы с лог-нормальным распределением. Нормальное распределение можно преобразовать в логарифмическое распределение с помощью логарифмической математики. Это прежде всего основа, поскольку логнормальное распределение может происходить только из нормально распределенного набора случайных величин.

Может быть несколько причин для использования логнормальных распределений в сочетании с нормальными распределениями. Как правило, большинство логнормальных распределений являются результатом натурального логарифма, где основание равно e = 2,718. Однако логнормальное распределение можно масштабировать с использованием другой базы, которая влияет на форму логнормального распределения.

В целом логнормальное распределение отображает логарифм случайных величин из кривой нормального распределения. В общем, журнал известен как показатель степени, до которого необходимо возвести базовое число, чтобы получить случайную величину (x), которая находится вдоль нормально распределенной кривой.

Для получения дополнительной информации см. Также статью Investopedia « Логнормальное и нормальное распределение».

Применение и использование логнормального распределения в финансах

Нормальные распределения могут представлять несколько проблем, которые могут решить логнормальные распределения. В основном нормальные распределения могут допускать отрицательные случайные величины, в то время как логнормальные распределения включают все положительные переменные.

Одним из наиболее распространенных приложений, где в финансах используются логнормальные распределения, является анализ цен на акции . Потенциальную доходность акции можно изобразить в виде нормального распределения. Тем не менее, цены на акции можно изобразить в виде логарифмически нормального распределения. Таким образом, кривая нормального логарифмического распределения может использоваться для более точного определения совокупной доходности, которую акция может ожидать за определенный период времени.

Обратите внимание, что логнормальные распределения имеют положительный перекос с длинными правыми хвостами из-за низких средних значений и высокой дисперсии случайных величин.

Логнормальное распределение в Excel

Логнормальное распределение можно выполнить в Excel . Он находится в статистических функциях как ЛОГНОРМ.РАСП.

Excel определяет это как следующее:

ЛОГНОРМ.РАСП (x; среднее; стандартное_откл; совокупное)

Возвращает логнормальное распределение x, где ln (x) нормально распределено с параметрами mean и standard_dev.

Для расчета ЛОГНОРМ.РАСП в Excel вам понадобится следующее:

x = значение, при котором оценивается функция

Среднее = среднее значение ln (x)

Стандартное отклонение = стандартное отклонение ln (x), которое должно быть положительным.

Источник

Проверка гипотезы о нормальном распределении логарифмической доходности по критерию Фроцини

Проверка гипотезы о нормальности распределения дневных логарифмических доходностей, рассчитанных по котировкам акций. Принятие в расчет достаточного объема выборок данных. Расчет характеристик временных рядов. Оценка статистического критерия Фроцини.

Рубрика	Экономико-математическое моделирование
Вид	курсовая работа
Язык	русский
Дата добавления	29.08.2015
Размер файла	307,0 K

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Размещено на http://www.allbest.ru/

1. Введение

2. Предварительный анализ данных

3. Теоретическая часть

3.1 Статистическая проверка гипотез

3.2 Статистический критерий Фроцини

4. Проверка гипотезы для модельных данных

5. Выбор альтернативной гипотезы и оценка мощности критерия

6. Проверка гипотез для реальных данных

Заключение

Список используемой литературы

Приложения

1. Введение

Курсовая работа состоит из двух основных частей. Первая часть представляет собой теоретическую справку, содержащую краткое описание применяемых в работе статистических критериев и методов. Вторая часть — практическая, состоит из проверки гипотезы на модельных данных, выбора альтернативной гипотезы и проверки мощности критерия, предварительного анализа реальных данных.

Необходимо сказать, что подобное исследование является крайне актуальным в наше время. Именно критерий Фроцини дает нам возможность понять, насколько близким к нормальному является исследуемое распределение.

Основными источниками литературы, используемыми при написании работы стали «Лекции по математической статистике» А.В. Браилова [1], «Прикладная математическая статистика. Для инженеров и научных работников» А.И. Кобзаря [2]. Были изучены курсовые работы прошлых лет.

2. Предварительный анализ данных

Таблица 1.

Список и наименование компаний

Authentidate Holding Corp.

Evolving Systems Inc.

Formula Systems (1985) Ltd.

Integrated Silicon Solution Inc.

The Ultimate Software Group, Inc.

В таблице 2 (программа 1) отражено количество дней, в которые акции торговались на бирже в период с 01.01.2010 г по 31.12.2014 г., а так же для индекса в целом.

В то же время при выборе исследуемого периода необходимо принять во внимание наличие резких скачков в ценах акций, вызванных сплитами — дроблениями или консолидациями акций, когда число находящихся в обращении акций увеличивается или уменьшается. В этих случаях номинальная стоимость акций соответственно резко уменьшается или резко увеличивается

Количество наблюдений. (Программа 1)

Также составим таблицу объёма торгов (количество проданных акций или сделок) по акциям тиккеров.

Объем торгов. (Программа 2)

Как видно из таблиц 2 и 3, все исследуемые акции торговались практически непрерывно на протяжении всего рассматриваемого периода времени, кроме выходных, число торговых дней по каждому тиккеру в целом совпадает с числом торговых дней фондового индекса, и объём торгов по ним был весьма высок.

Для того, чтобы убедиться в достоверности исследуемых данных, сопоставим графики курса акций каждого тиккера и курса фондового индекса IXCO за весь рассматриваемый промежуток времени. (Программа 3)

нормальное распределение логарифмическая доходность

Эта несложная проверка подтверждает достоверность исследуемых данных

Далее вычислим некоторые характеристики временных рядов.

Рассчитаем волатильность, характеризующую тенденцию рыночной цены, изменяющуюся во времени.

Таблица 4. Волатильность. (Программа 3)

Рассчитаем максимальные относительные скачки цен в каждом году.

Таблица 5. Максимальные относительные скачки. (Программа 4)

Рассчитаем бета-коэффициент для каждого тиккера за весь промежуток времени. для того чтобы отразить изменчивость доходности ценной бумаги по отношению к доходности рынка в среднем

3. Теоретическая часть

Таким образом, статистической гипотезой называется любое утверждение о виде или параметрах генерального распределения.

Проверка статистической гипотезы — это процесс принятия решения о том, противоречит ли рассматриваемая статистическая гипотеза наблюдаемой выборке данных.

Пусть и — две взаимоисключающие статистические гипотезы. Гипотезу назовем основной, а гипотезу — альтернативной. Как правило, в качестве базисного предположения принимается утверждение о справедливости одной из гипотез.

Статистическим критерием с критической областью называется правило, в соответствии с которым отвергается, если выборка , и принимается, если . Другими словами, статистический критерий представляет собой специально подобранную случайную величину, точное или приближенное которой известно. В свою очередь, критическая область — это совокупность значений статистического критерия, при которых нулевая гипотеза отвергается. Областью принятия гипотезы, называется совокупность значений статистического критерия, при которых нулевая гипотеза принимается.

Применение статистического критерия может привести к ошибкам двух различных типов:

· ошибка первого рода состоит в том, что отвергается верная гипотеза

· ошибка второго рода состоит в том, что отвергается верная гипотеза

Вероятность ошибки первого рода называется уровнем значимости критерия и обозначается . Вероятность ошибки второго рода обозначается , а величина называется мощностью критерия.

Необходимо отметить, что с распространением статистических программ возникает понятие, которое позволяет решить вопрос о принятии или отклонении основной гипотезы одновременно для всех уровней значимости без вычисления критических значений. Так для фиксировано реализации случайной выборки

Р-значением (Р-value) называется такое число , что для любого уровня значимости , при котором гипотеза принимается, и для любого уровня значимости , при котором гипотеза отвергается.

3.2 Статистический критерий Фроцини

Фроцини предложил простой, но достаточно мощный критерий нормальности с параметрами, оцениваемыми по выборке, основанный на статистике

Рассмотрим математическую составляющую критерия Фроцини.

Критерий Фроцини — основной статистический критерий

Критерий Фроцини является мощным критерием нормальности с параметрами, оцениваемыми по выборке, основанном на статистике

— порядковые статистики, а — функция распределения стандартного нормального закона N (0,1).

Критерий Колмогорова — вспомогательный критерий

В качестве вспомогательного критерия по проверке равномерности распределения Р-значения основного критерия в данной работе используем критерий Колмогорова.

Критерий Колмогорова рассматривает максимальное значение модуля разности между статистической функцией распределения и соответствующей теоретической функцией распределения F (x, т.е. D = .

Следующим шагом определяется величина . По статистическим таблицам (в среде matcalc функцией рvKolm (u)) находится вероятность того, что за счет чисто случайных причин максимальное расхождение между и F (x) будет не меньше, чем фактически наблюденное. Если вероятность Р () сравнительно велика, то гипотезу следует принять, если весьма мала, то отвергнуть как неправдоподобную.

4. Проверка гипотезы для модельных данных

Для того чтобы проверить гипотезу о нормальном распределении:

1. С помощью программы «Квантали. mtc« методом Монте-Карло вычисляются квантили распределения статистики Фроцини. Результаты представлены в следующей таблице:

Таблица 7. Квантили распределения основной статистики.

2. С помощью программы «Р-значения. mtc« вычисляются Р-значения и приводится их гистограмма.

Рисунок 1. Р-значения на модельных данных. (Программа 7)

Как мы можем видеть из рисунка, Р-значения распределены довольно равномерно, что позволяет говорить о том, что гипотеза о нормальности распределения модельных данных по исследуемому критерию Фроцини принимается.

3. В программе «Р-значения. mtc» производится проверка равномерности распределения Р-значения на отрезке [0; 1] по критерию Колмогорова.

В результате выполнения программы мы получаем значение 0,990255. С одной стороны, можно говорить о том, что полученное значение не в полной мере подтверждает равномерность распределения. Однако было замечено, что это напрямую связано с частотой вычисления статистики (в нашем случае — 10000 раз, при снижении — критерий Колмогорова все более стремится к единице). Поэтому равномерность, на мой взгляд, можно считать доказанной.

5. Выбор альтернативной гипотезы и оценка мощности критерия

Оценим на основе 1000-кратной проверки нулевой гипотезы при верной альтернативной мощность критерия Фроцини для выбранного распределения с помощью программы «Прог8. мощность критерия. mtc«. В результате работы программы мы получаем, что, например, при 5% уровне значимости мощность составит 0,766, а при 1% уровне значимости — 0,621

Таким образом, мощность критерия достаточно велика, а значит, при использовании критерия Фроцини, вероятность совершить ошибку второго рода, то есть принять неправильную гипотезу, мала.

6. Проверка гипотез для реальных данных

Рисунок 2. Р-значения на реальных данных.

Очевидно Р-значения распределены неравномерно, а значит мы можем говорить о том, что гипотеза о нормальности отвергается.

2. Вычисляется доля проверок, в которых гипотеза принималась при 5% и 1% уровнях значимости. Было получено, что

· при 5% уровне значимости гипотеза принимается в 14,5% случаев

· при 1% уровне значимости гипотеза принимается в 25,5% случаев

Таким образом, нет необходимости переходить к исследованию данных за второе полугодие.

3. Вычисляются медианные Р-значения по годам и компаниям.

Источник