Норма доходности по финансовым рынкам

Требуемая норма доходности – RRR

Что такое Требуемая норма доходности – RRR?

Требуемая норма прибыли – это минимальный доход, который инвестор примет за владение акциями компании в качестве компенсации за определенный уровень риска, связанного с владением акциями. RRR также используется в корпоративных финансах для анализа прибыльности потенциальных инвестиционных проектов.

Требуемая норма прибыли также известна как пороговая ставка , которая, как и RRR, обозначает соответствующую компенсацию, необходимую для существующего уровня риска. Более рискованные проекты обычно имеют более высокие пороговые ставки или RRR, чем менее рискованные.

Формула и расчет RRR

Есть несколько способов рассчитать требуемую норму прибыли. Если инвестор рассматривает возможность покупки акций компании, которая выплачивает дивиденды, модель дивиденд-дисконт является идеальной. Модель дисконтирования дивидендов также известна как модель роста Гордона .

Модель дисконтирования дивидендов рассчитывает RRR капитала для акций, выплачивающих дивиденды, с использованием текущей цены акций, выплаты дивидендов на акцию и прогнозируемого темпа роста дивидендов. Формула выглядит следующим образом:

Расчет RRR с использованием модели скидки на дивиденды.

1. Возьмите ожидаемую выплату дивидендов и разделите ее на текущую цену акций.
2. Добавьте результат к прогнозируемым темпам роста дивидендов.

Другой способ расчета RRR – использовать модель ценообразования капитальных активов (CAPM), которая обычно используется инвесторами для акций, по которым не выплачиваются дивиденды.

Модель расчета RRR CAPM использует бета-коэффициент актива. Бета – коэффициент риска холдинга. Другими словами, бета-версия пытается измерить рискованность акций или инвестиций с течением времени. Акции с бета-коэффициентами больше 1 считаются более рискованными, чем рынок в целом (представленный S&P 500), тогда как акции с бета-коэффициентами меньше 1 считаются менее рискованными, чем рынок в целом.

В формуле также используется безрисковая норма доходности, которая обычно представляет собой доходность краткосрочных ценных бумаг Казначейства США. Последняя переменная – это рыночная ставка доходности, которая обычно является годовой доходностью индекса S&P 500. Формула для RRR с использованием модели CAPM выглядит следующим образом:

Расчет RRR с использованием CAPM

1. Добавьте текущую безрисковую норму прибыли к бета-версии безопасности.
2. Возьмите рыночную норму доходности и вычтите безрисковую норму доходности.
3. Добавьте результаты, чтобы получить требуемую доходность.

Вычтите безрисковую норму прибыли из рыночной нормы прибыли.

Возьмите этот результат и умножьте его на бета-версию безопасности.

Добавьте результат к текущей безрисковой норме доходности, чтобы определить требуемую норму доходности.

Ключевые моменты

• Требуемая норма прибыли – это минимальная доходность, которую инвестор примет за владение акциями компании, которая компенсирует им заданный уровень риска.
• Инфляция также должна учитываться при расчете RRR, который определяет минимальную норму прибыли, которую инвестор считает приемлемой, принимая во внимание стоимость капитала, инфляцию и доходность других инвестиций.
• RRR – это субъективная минимальная норма прибыли, и пенсионер будет иметь более низкую толерантность к риску и, следовательно, получит меньшую прибыль, чем инвестор, недавно окончивший колледж.

Что вам говорит RRR?

Для инвесторов, использующих формулу CAPM, требуемая норма доходности для акций с высоким бета-коэффициентом относительно рынка должна иметь более высокий RRR. Более высокий RRR по сравнению с другими инвестициями с низкой бета-версией необходим для компенсации инвесторам дополнительного уровня риска, связанного с инвестированием в акции с более высокой бета-версией.

Другими словами, RRR частично рассчитывается путем прибавления премии за риск к ожидаемой безрисковой норме доходности для учета дополнительной волатильности и последующего риска.

Для капитальных проектов показатель RRR полезен при определении того, следует ли развивать один проект по сравнению с другим. RRR – это то, что необходимо для продолжения проекта, хотя некоторые проекты могут не соответствовать RRR, но отвечают долгосрочным интересам компании.

Инфляция также должна быть учтена при анализе RRR. RRR на акцию – это минимальная норма прибыли на акцию, которую инвестор считает приемлемой, принимая во внимание стоимость капитала , инфляцию и доходность других инвестиций.

Например, если инфляция составляет 3% в год, а премия за риск по акциям превышает безрисковую доходность (с использованием казначейского векселя США с доходностью 3%), то инвестору может потребоваться доход в размере 9% в год для выпуска акций. стоящие инвестиции. Это связано с тем, что доходность 9% на самом деле является доходностью 6% после инфляции, а это означает, что инвестор не будет вознагражден за риск, который они приняли. Они получат такую ​​же скорректированную с учетом риска доходность, инвестируя в казначейские векселя с доходностью 3%, которые будут иметь нулевую реальную норму прибыли после поправки на инфляцию.

Примеры RRR

Ожидается, что в следующем году компания будет выплачивать ежегодные дивиденды в размере 3 долларов, а ее акции в настоящее время торгуются по 100 долларов за акцию. Компания ежегодно стабильно увеличивает дивиденды со скоростью 4%.

• RRR = 7% или ((ожидаемые дивиденды 3 доллара / 100 долларов на акцию) + темп роста 0,04)

В модели ценообразования капитальных активов (CAPM) RRR может быть рассчитан с использованием бета-коэффициента ценной бумаги или коэффициента риска, а также избыточная доходность, которую приносит инвестирование в акции по безрисковой ставке, является премией за риск по акциям .

RRR с использованием примера формулы CAPM

• Компания имеет бета-версию 1,50, что означает, что она более рискованна, чем бета-версия, равная единице для всего рынка.
• Текущая безрисковая ставка составляет 2% по краткосрочным казначейским облигациям США.
• Долгосрочная средняя доходность для рынка составляет 10%.
• RRR = 14% или (0,02 + 1,50 x (0,10 – 0,02)).

RRR против стоимости капитала

Хотя требуемая норма прибыли используется в проектах капитального бюджета, RRR – это не тот уровень прибыли, который необходим для покрытия стоимости капитала . Стоимость капитала – это минимальный доход, необходимый для покрытия стоимости заемных средств и выпуска акций для сбора средств для проекта. Стоимость капитала – это самая низкая доходность, необходимая для учета структуры капитала. RRR всегда должен быть выше стоимости капитала.

Ограничения RRR

Расчет RRR не учитывает инфляционные ожидания, поскольку рост цен снижает инвестиционную прибыль. Однако инфляционные ожидания субъективны и могут ошибаться.

Кроме того, RRR будет варьироваться между инвесторами с разным уровнем толерантности к риску. Пенсионер будет менее терпимым к риску, чем инвестор, недавно окончивший колледж. В результате RRR – это субъективная норма прибыли.

RRR не учитывает ликвидность инвестиции. Если инвестиция не может быть продана в течение определенного периода времени, ценная бумага, вероятно, будет нести более высокий риск, чем более ликвидная.

Кроме того, сравнение акций в разных отраслях может быть затруднительным, поскольку риск или бета будут разными. Как и в случае с любым финансовым коэффициентом или показателем, при рассмотрении инвестиционных возможностей лучше всего использовать несколько коэффициентов в своем анализе.

Источник

Расчет рыночной доходности

Формула расчета рыночной доходности

Любому, кто занимается вложением средств, необходимо уметь грамотно рассчитывать доходность — как для собственных нужд, так и для правильного прочтения различных источников, где указываются результаты инвестиций. В самом простом случае — банковского депозита — рост дохода происходит по прямой линии и сложных расчетов не требуется.

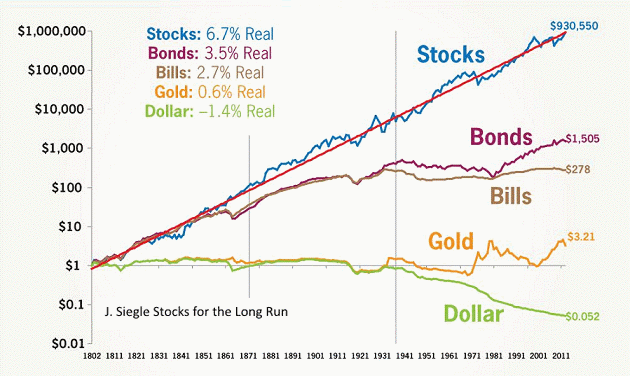
Однако если мы возьмем банковский депозит с возможностью капитализации процентов, то картина уже изменится: счет начнет расти по экспоненте. Аналогичный, но более сильный эффект дает инвестирование на фондовом рынке в акции (логарифмическая шкала):

Вообще говоря, в сети нетрудно найти калькулятор сложного процента — но подойдет он отнюдь не для каждой задачи и поскольку содержит формулу в закрытом виде, то не дает понимания о сути расчета. Непонимание работы с рыночными данными способно привести к ошибкам даже в самых простых случаях. Ниже мы рассмотрим, как посчитать доходность в процентах для разных случаев.

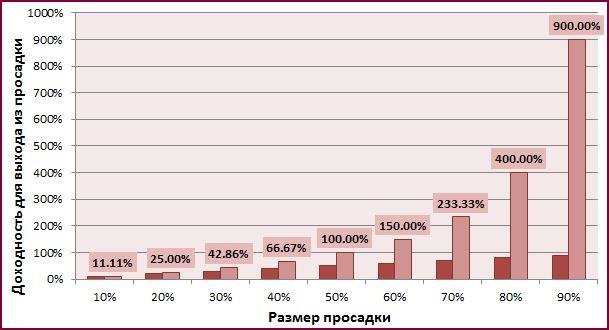
Из этого следует очень важное правило: чем выше просадка, тем большая доходность требуется, чтобы ее отыграть . К примеру, если стоимость актива за год уменьшилась на 80% (осталось только 20% начальной цены), то требуется доходность в целых 400%, чтобы достичь первоначального уровня:

Именно поэтому агрессивные стратегии с высоким кредитным плечом не живут долго — математическое ожидание даже при большей вероятности прибыли, чем убытка все равно со временем уничтожит депозит.

В общем случае формула доходности выглядит так:

A(n) = A(n-1) × (1 + X) = A(0) × (1 + X)^n или X = (A(2)/A(0))^(1/n) – 1

1. A(0) – исходное количество денег
2. А(n) – количество денег через n лет
3. X – годовая доходность (в процентах)

Если же взять изменение за год в разах (Y) (т.е. мы рассматриваем изменение на 10% как рост в 1,1 раза, Y = 1 + 10/100 = 1,1), то

A(n) = A(n-1) × Y = A(0) × Y^n

Задача

Актив растет на 10% в год. Какова будет его доходность через 2 года?

Можно искать калькулятор сложного процента, а можно сказать, что Y = 1.1, число лет n = 2. Тогда взяв исходное количество денег за условную единицу

А(2) = 1 × 1.1² = 1.21, т.е. актив вырастет на 21% (из 1000 рублей будет 1210)

Обратная задача

Найти среднюю годовую доходность при росте актива на 21% в течение двух лет (понятно, что она может расти неравномерно — мы же найдем среднюю величину):

Снова принимая нашу первоначальную доходность за условную единицу, считаем:

Y = (1.21/1)½ = 1.1, т.е. усредненная доходность равна 10%

Задача 2

За четыре года банковский вклад с ежегодной капитализацией прибыли вырос от 100.000 рублей до 150.000 рублей. Какова средняя доходность в годовом исчислении?

Y = (150.000/100.000)^(1/4) = 1.10668, т.е. средняя годовая доходность равна 10.67%

Соответственно, просто разделив 50% на 4 мы получили бы среднеарифметическую доходность 12.5%, что неверно. Эта разница и есть преимущество сложного процента: без него доходность каждый год начислялась бы на 100.000 рублей — т.е. каждый год мы получали бы 12.500, что за четыре года и даст ровно 50.000. Однако при ежегодной капитализации мы добиваемся того же результата уже с меньшим процентом (10.67%).

Задача 3

За 2 года и 6 месяцев стоимость пая в инвестиционном фонде выросла на 42.7% (допустим, пай стоил 5 рублей, а стал стоить 7.135 рубля — значит, 7.135/5 = 1.427). Какова средняя доходность фонда в год?

2 года и 6 месяцев это 2.5 года (n = 2.5), а Y = 1.427. Тогда

Y = (1.427/1)^(1/2.5) = 1.1528, т.е. средняя годовая доходность равна 15.28%

Если за «n» обозначить количество месяцев (n = 30), то теперь можно вычислить и среднемесячную доходность (1.427^(1/30) = 1.0119 или 1.19%. При этом среднеарифметическая доходность была бы 42.7/30 = 1.4233%). Если мы возьмем банковский депозит, где капитализация происходит ежемесячно, то считать надо в месяцах, если ежегодно — то в годах.

Задача 4

Значение индекса ММВБ на конец декабря 1997 года – 85.05 пунктов. Значение индекса ММВБ на конец 2007 года – 1888.86 пунктов. Какова среднегодовая доходность индекса ММВБ за 10 лет?

Y = (A(2)/A(0))^(1/n) = (1888.86/85.05)^(1/10) = 1.3635 или 36.35%

Задача 5

Ниже дана российская инфляция за 2000-2007 годы. Нужно рассчитать среднегодовую.

2000 г. – 20,2%
2001 г. – 18,6%
2002 г. – 15,1%
2003 г. – 12,0%
2004 г. – 11,7%
2005 г. – 10,9%
2006 г. – 9,0%
2007 г. – 11,9%

Это как раз случай, хорошо приближенный к реальности — доходность фондового рынка можно смотреть как по разнице пунктов за выбранный промежуток времени, так и считать (или брать из справочника) по годам. Тогда общий рост потребительской корзины:

1,202 × 1,186 × 1,151 × 1,120 × 1,117 × 1,109 × 1,090 × 1,119 = 2,777 раза (или на 177%)

И средняя инфляция

Y = (A(2)/A(0))^(1/n) =2.777^(1/8) = 1.1362 или 13.62%

P.S. Задача аналогично может быть использована для расчета средней доходности активов, которая за год бывает отрицательной. В этом случае коэффициент берется меньше 1, например при доходности минус 10% в год он равен 1 — 10/100 = 0.9.

Задача 6

Инвестор входит в некоторый счет, который показывает в текущий момент 1500%. Выходит из него через полгода, когда показатель достигает 1700%. Пусть он инвестировал 500 долларов и получил 70% от роста котировок. Каков его доход в % годовых и по абсолютной величине?

Это не 200%, умноженные на 0.7! Считаем: (1 + 1700/100)/(1 + 1500/100) и получаем 1.125, т.е. 12.5% за полгода. Следовательно, среднеарифметически в год будет в два раза больше, а среднегеометрически 1.125^(1/0.5) = 26.56%. Хотя такой расчет в этом случае не будет корректен — мы экстраполируем прибыль, т.е. считаем не только имеющийся, но и будущий результат.

Как видно, в этом случае среднегеометрическая доходность получается выше среднеарифметической — так что таким приемом иногда пользуются инвестиционные фонды, экстраполируя удачные квартальные результаты на целый год. Если же нужно рассчитать доход на 500 долларов за время инвестирования, то сначала учтем, что инвестор получает лишь 70% от роста, т.е. 12.5% × 0.7 = 8.75%. Следовательно, прибыль равна 500 × 8.75% / 100% = 43.75 долларов.

Похожий пример: вошли в счет на отметке доходности в 30%, вышли на 90%. При этом прибыль инвестора увеличилась не в три раза, а на (1 + 90/100)/(1 + 30/100) ≈ 1.46, т.е. примерно на 46%. Если взять 500 долларов, инвестированные в счет, то суммарный баланс составит примерно 730 долларов (прибыль около 230 $).

Задача 7

Расчет доходности акций с учетом дивидендов и курсового роста стоимости. Пусть была куплена акция одной компании за 120 рублей. Спустя какое-то время по ней получены дивиденды 7.2 рубля, а котировки выросли до 135 рублей — после чего акцию продали. Рассчитать полученный доход.

Y = [(7.2 + (135-120))/120] × 100% = 18.5%

Задача 8

По данным предыдущего примера рассчитать доходность в процентах годовых, если на момент продажи акции (достижения ее стоимости 135 рублей) прошло 250 дней:

Y = [(7.2 + (135-120))/120] × 365/250 × 100% = 27.01%

Источник