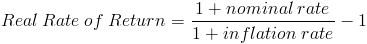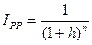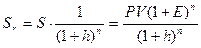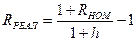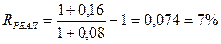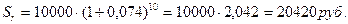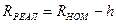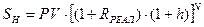Номинальную ставку доходности темпы инфляции

Как правильно считать реальную доходность с учетом инфляции?

Автор: Алексей Мартынов · Опубликовано 03.07.2015 · Обновлено 02.12.2018

Наверно все знают, что реальная доходность — это доходность за вычетом инфляции. Все дорожает — продукты, товары, услуги. По данным Росстата за последние 15 лет цены выросли в 5 раз. Это означает, что покупательная способность денег, просто лежавших все это время в тумбочке уменьшилась в 5 раз, раньше могли купить 5 яблок, теперь 1.

Чтобы хоть как-то сохранить покупательную способность своих денег, люди их вкладывают в различные финансовые инструменты: чаще всего это депозиты, валюта, недвижимость. Более продвинутые используют, акции, ПИФы, облигации, драгметаллы. С одной стороны сумма вложений растет, с другой происходит их обесценивание из-за инфляции. Если из номинальной ставки доходности вычесть ставку инфляции, получится реальная доходность. Она может быть положительной или отрицательной. Если доходность положительная, ваши вложения приумножились в реальном выражении, то есть вы можете купить больше яблок, если отрицательная — обесценились.

Большинство инвесторов считают реальную доходность по простой формуле:

Но данный способ неточен. Приведу пример: возьмем 200 рублей и положим их на депозит на 15 лет со ставкой 12% годовых. Инфляция за этот период 7% в год. Если считать реальную доходность по простой формуле, то получится 12-7=5%. Проверим этот результат, посчитав на пальцах.

За 15 лет при ставке 12% годовых 200 рублей превратятся в 200*(1+0,12)^15=1094,71. Цены за это время вырастут в (1+0,07)^15=2,76 раз. Чтобы посчитать реальную доходность в рублях делим сумму на депозите на коэффициент инфляции 1094,71/2,76=396,63. Теперь, чтобы перевести реальную доходность в проценты считаем (396,63/200)^1/15 -1 *100% = 4,67%. Это отличается от 5%, то есть проверка показывает, что расчет реальной доходности «простым» способом не точен.
Чтобы правильно рассчитать реальную доходность, нужно применять формулу:

Real Rate of Return — реальная доходность
nominal rate — номинальная ставка доходности
inflation rate — инфляция

Проверяем:
(1+0,12)/(1+0,07)-1 * 100%=4,67% Сходится, значит формула верная.

Еще одна формула, которая дает тот же результат, выглядит так:

Источник

Номинальную ставку доходности темпы инфляции

Сегодня мы последовательно обсудим разницу, незримо присутствующую между номинальными и реальными процентными ставками.

Для этого нам понадобиться припомнить, что такое инфляция, и познакомиться с новым понятием – индексом потребительских цен.

Попутно пополним наш арсенал несколькими элементарными формулами, которые позволят в два счета оценивать реальную доходность наших инвестиций.

Итак, отправная точка – инфляция.

Пункт назначения – четкое понимание разницы между номинальными процентными ставками и неразрывно связанными с ними реальными, между номинальной стоимостью денег и реальной, между номинальными доходами и реальными…

Что такое инфляция?

Нестрогое определение инфляции таково: это обесценивание покупательной способности денег с течением времени.

Численной мерой инфляции служит изменение из года в год индекса потребительских цен (общеупотребительное сокращение — ИПЦ), отвечающего на вопрос, сколько среднестатистическая семья вынуждена тратить денег на приобретение некоторой группы товаров.

Процесс, обратный инфляции, а именно, увеличение покупательной способности денег из-за снижения цен, именуется дефляцией.

Это явление было характерно, к примеру, для периода Великой депрессии (кон.1920-х – нач.1930-х гг.) в Соединенных Штатах, когда падение цен на большинство услуг и товаров за год доходило до 10 процентов.

Редчайший, надо сказать, случай в истории экономики США, повторения которого с тех пор так и не удалось достичь…

Номинальная стоимость денег

Суть инфляции хорошо воспринимается на классических примерах, заимствованных нами из недр экономической теории.

Для начала проиллюстрируем, что такое номинальная стоимость денег и что такое номинальная процентная ставка.

Представьте себя инвестором, разместившим 650 долл. на банковском вкладе либо приобретшим сберегательный сертификат на ту же сумму.

Годовая процентная ставка по вкладу (сертификату), положим, равняется 8 %.

Соответственно, ваши обоснованные ожидания по части приумножения капитала легко рассчитать: 650 долл. * 1,08 = 702 долл. (+52 долл.).

Банк, разумеется, выполнит свои обязательства и облагодетельствует вас обещанными суммами.

Но чего банк точно не сможет сделать, так это гарантировать вам сохранение уровня цен, действовавшего на момент открытия вклада (приобретения сертификата), до момента его закрытия (погашения сертификата).

Другими словами, банк не сможет вам обещать, что по итогам инвестиционного года вы станете БОГАЧЕ.

Все потому, что банк прекрасно осведомлен о неуемном аппетите матушки-инфляции, которая не щадит ни вкладчиков, ни банкиров, ни бедных (что вполне объяснимо), ни – что менее очевидно — богатых.

Может так статься, что рост инфляции окажется выше 8 %, и тогда, несмотря на номинальный прирост капитала, вы в конечном итоге окажетесь беднее…

702 долл., о которых мы вели речь выше, являют собой НОМИНАЛЬНУЮ стоимость ваших сбережений. Соответственно, 8% — это номинальная процентная ставка.

Для перехода к реальным процентным ставкам нам придется прибегнуть к некоторым несложным вычислениям, представленным далее.

Формула расчета реальной стоимости денег

Чтобы рассчитать реальную стоимость ваших денег по истечении инвестиционного периода, уместно воспользоваться следующей формулой:

R = N / (1 + i) n , где

R – реальный денежный поток,
N – номинальный денежный поток,
i – инфляционная процентная ставка,
n – количество лет.

Представим, что ежегодный рост цен на товары и услуги (то бишь размер инфляции) составляет 5 %.

При таких исходных данных реальная стоимость оказавшегося в нашем распоряжении капитала составит 668,57 долл.:

702 долл. / (1 + 0,05) = 668,57 долл.

По итогам наших инвестиций НОМИНАЛЬНО мы стали богаче на 52 долл., а РЕАЛЬНО – всего лишь на 18,57 долл.

Если бы срок нашего депозита составил бы 10 лет, то при тех же ставках доходности по вкладу и инфляции реальная выручка была бы такой:

N = 650 долл. * (1 + 0,08) 10 = 1403,3 долл.

R = 1403,3 долл. /(1 + 0,05) 10 = 861,5 долл.

Другими словами, номинально мы станем богаче более чем в 2 раза, а реально – лишь на чуть более 30 %…

Расчет реальной процентной ставки

Из наших вычислений становится понятным, как находить реальную процентную ставку (реальную доходность инвестиций). Формула должна иметь примерно такой вид:

1 + r_{реальн.} = (1 + r_номин.) n / (1 + i) n , где

r_{реальн.} – реальная процентная ставка,
r_{реальн.} – номинальная процентная ставка,
i – инфляционная процентная ставка,
n – количество лет.

Умножая на полученный коэффициент исходную сумму или исходный размер капитала, можно легко рассчитать реальную доходность инвестиций с поправкой на инфляцию.

Вот, собственно, и вся теория по теме номинальных и реальных процентных ставок.

Приведенные формулы легко приспособить и для случаев, когда инвестиционные отчисления носят характер аннуитета.

В этом вопросе лучше попробовать разобраться самостоятельно.

Источник

НОМИНАЛЬНЫЕ И РЕАЛЬНЫЕ ПРОЦЕНТНЫЕ СТАВКИ В УСЛОВИЯХ ИНФЛЯЦИИ

По определению, номинальная процентная ставка показывает каким-либо образом оговоренную ставку доходности по инвестиро­ванным или ссуженным денежным суммам и рост этой суммы за оп­ределенный период времени в процентах. В отличие от номинальной реальная процентная ставка показывает рост покупательной способ­ности первоначально инвестированных или ссуженных денежных сумм с учетом как номинальной процентной ставки, так и темпа ин­фляции, т.е. характеризует изменение реальной стоимости денег.

Показатель реальной стоимости денег обратно пропорционален ин­дексу инфляции, т.е. среднегодовому индексу прироста цен (при ана­лизе инфляции, как правило, рассматриваются потребительские цены). Если принять, что индекс инфляции (среднегодовой индекс прироста цен) равен h и что он не меняется год от года, то за п лет индекс цен будет равен (1 + h) n , а индекс покупательной способности денег:

Тогда реальная стоимость S_r номинальной наращенной суммы S составит:

где: РV — первоначальная денежная сумма.

Таким образом, реальная стоимость денег в будущем тем больше, чем выше процентная ставка, и тем меньше, чем выше индекс инфляции.

Очевидно, что и уровень инфляции, и процентная ставка на прак­тике не остаются неизменными в течение длительного периода. Это также может быть отражено в формуле расчета реальной стоимости денег в будущем, если несколько усложнить ее, не изменив сути и характера зависимости этого показателя от процентной ставки и уровня инфляции.

Таким образом, формула, позволяющая определить величину реальной процентной ставки, будет иметь вид:

где: R _НОМ — номинальная процентная ставка;

h — темп инфляции.

Пример 9.1.: Индекс инфляции равен 8 % в год; сумма 10000 рублей вложена под 16% годовых на 10 лет. Нужно определить реальную процентную ставку и реальную стоимость денег.

или

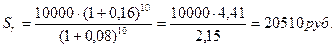
При невысоких темпах инфляции и процентных ставках (менее 10%в год) можно пользоваться упрощенной формулой

Будущая стоимость денежных средств с учетом фактора инфляции (номинальная стоимость) определяется по формуле:

Пример: Первоначальная сумма вклада составляет 100000 руб;

Реальная процентная ставка 10%, прогнозируемый темп инфляции 6 % в год;

Вклад размещен на 5 лет, при начислении процентов раз в год. Определить номинальную будущую стоимость вклада с учетом инфляции?

S_H =100000[(1+0,1) (1+0,06)] 5 =100000ּ2,156=215600 руб.

9.3 ВЛИЯНИЕ ИНФЛЯЦИИ НА ДОХОДЫ ФИРМ .

Особая тема — как инфляция может изменить доходность ин­вестиций и соответственно как это обстоятельство надо учитывать при анализе приемлемости проектов.

Если исходить из того, что в результате инвестирования исходная сумма средств I₀ должна возрасти в пропорции (1 + E),где E — реальная норма прибыли на инвестиции, то в условиях инфляции (величину которой в процентах мы обозначим h) все это будет выглядеть несколь­ко иначе. Действительно, в последнем случае новая (приращенная) величина инвестированных сумм I₁, будет равна

Читайте также:  Пайер майнинг кошелек без вложений

Где: произведение (1 + E)(1+h) будет обозначать совокупный (номи­нальный) рост инвестиций в результате как собственно удачной их реализации, так и под влиянием инфляционного роста цен на товары, произведенные благодаря этим инвестициям.

В этом случае результат инвестиционной деятельности можно было бы записать:

Где: Eп — номинальная ставка прибыльности проекта.

Таким образом, номинальная доходность инвестиционного проекта в условиях инфляции складывается из реальной нормы прибыли, темпа инфляции и реальной нормы прибыли, умноженной на темп инфляции.

Пример 9.2.: Предположим, мы имеем дело с проектом, обеспечивающим реальный уровень прибыльности на уровне 10% и реализованным в условиях 5%-ной инфляции (в годовом исчислении). Определить номинальная доход­ность проекта?

Номинальная доход­ность составит (в долях):

Е _n =E+h+Eּh =0,10 + 0,05 + 0,1 • 0,05 = 0,155.

Нетрудно подсчитать, что из общего размера дохода в 15,5% на долю инфляционной составляющей пришлось 5,5 пунктов, т.е. 35,5%.

Но главной особенностью инвестиций в реальные активы является вложение средств сегодня ради получения выигрыша в будущем, причем срок жизни таких ин­вестиций обычно более года. Отсюда — неодновременность осуществления затрат и получения дохода, и чем больше этот разрыв, тем сильнее инвестиционный проект подвержен воздействию инфляционных процессов. Рассмотрим различные ситуации, которые здесьмогут возникать.

1. Рост реальной нормы прибыли при снижении инфляции..

Если вложения в проект растянуты во времени, то под влиянием инфляции цены на приобретаемые ресурсы и ре­ализуемую продукцию меняются достаточно близкими темпами. Тогда номинальный доход ока­зывается нечувствителен к инфляции и практически не меняется. А поскольку инфляция снижается, то в соответствии с выве­денной выше зависимостью уровень реальной доходности проекта при снижении инфляции начинает возрастать

2. Стабильность реальной нормы доходности при снижении инфля­ции.

Если в условиях затухающей инфляции цены на реализуемую продукцию снижаются быстрее, чем на приоб­ретаемые ресурсы, номинальный доход начинает падать.

Но если темп инфляции падает в большей мере, чем разница в средних индексах снижения доходов и затрат, то в соответствии с вы­веденной выше зависимостью уровень реальной доходности проекта при снижении инфляции может остаться стабилен.

3. Снижение реальной нормы доходности при снижении инфляции.

Если в условиях затухающей инфляции цены на реализуемую продукцию снижаются значительно быстрее, чем на приобретаемые ресурсы, то номинальный доход начинает падать также ускоренными темпами. И если темп инфляции падает в меньшей мере, чем разница в средних индекcax снижения доходов и затрат, то в соответствии с выведенной выше зависимостью уровень реальной доходности проекта при снижении инфляции также начинает понижаться.

Это означает, что при макроэкономической ситуации, когда име­ются основания ожидать резкого снижения инфляции, предпочтение следует отдавать проектам, для которых инвестирование не концент­рируется в начальной момент времени, а более растянуто во времени. Притаком эшелонировании вложений на затратах в большей мере сказывается эффект снижения темпов роста цен и разрыв между дина­микой дисконтированных затрат и дисконтированных результатов уменьшается. А следовательно, снижается и опасность убыточности проектов из-за сильной чувствительности к инфляции.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник