Номинальная доходность портфеля это

Как не ошибиться, рассчитывая среднюю доходность инвестиций, что такое «подножка волатильности», и почему умелая диверсификация не только обеспечивает стабильность инвестиционного портфеля, но и улучшает доходность.

Все инвесторы сталкиваются с необходимостью расчета средней доходности своего портфеля. Это нужно для того чтобы прогнозировать его будущую стоимость. Без такого прогноза невозможно, например, решить, на какую сумму следует пополнять инвестиционный портфель, чтобы достичь поставленных целей к сроку.

Часто инвесторы ошибаются в расчетах, потому что используют неправильную формулу. Использовать ошибочную оценку в планировании будущих действий опасно. Ценой просчета может стать качество жизни в старости или образование ребенка.

Как правильно оценить среднюю доходность

Среднюю доходность портфеля в заданном периоде нужно считать не как среднюю арифметическую, а как среднюю геометрическую. Разберемся на простом примере.

Допустим инвестор вкладывает деньги в российские акции через фонд А и российские облиции через фонд Б в пропорциях 60 на 40. Ниже в таблице приведены данные по ежегодной динамике стоимости акций, облигаций и совокупного портфеля.

Таблица №1. Доходности фондов А, Б и портфеля 60/40 за 4 года (в руб).

Инструмент	2016	2017	2018	2019
Фонд А	28,67%	-2,22%	16,74%	37,44%
Фонд Б	15,24%	14,83%	2,7%	15,34%
Портфель 60/40	23,30%	4,60%	11,12%	28,60%

Акции, облигации и портфель за все время принесли 101,86%, 56,74% и 83,81%. На первый взгляд получается 20,16%, 12% и 16,9% в среднем за год. На самом же деле эти цифры завышены. Как так вышло? Дело в том, что арифметическая средняя (сумма доходностей, поделенная на количество периодов) не походит для расчета инвестиционных результатов, так как доходность, полученная в очередном периоде, относится к стоимости портфеля в предыдущем периоде, и включает доходность на доходность прошлого периода, а не только на сумму инвестиций. Например, если портфель упал на 5% за период с уровня 10000, а затем поднялся на 5%, он не вернется к 10000, а будет стоить 9975 руб. В этом примере разница небольшая, но чем больше рыночная нестабильность, то тем больше будет расхождение. — это прекрасно видно на примере фонда А, который является более волатильным, чем фонд Б.

Для того, чтобы правильно учесть волатильность доходностей и их влияние на результат используют среднюю геометрическую или, как еще её называют, аннуализированную доходность (Compound Average Growth Rate). Она рассчитывается как корень степени n из произведения доходностей за n периодов. Например, ∜(1,232 * 1,046 * 1,1112 * 1,286) даст среднюю доходность портфеля в 16,5% в год (а не 16,7%, как средняя арифметическая). Как и средняя арифметическая, средняя геометрическая не всегда соответствует показателю в каждый конкретный год, но при этом в конце периода она трансформирует первоначально инвестированную сумму в точный итоговый результат инвестирования. Как следствие, именно этот показатель, а не среднюю арифметическую доходность стоит использовать для долгосрочного инвестиционного планирования. Сравнение динамики средней арифметической и реальной доходностей представлены в таблице №2 и на графике №1.

График №1. Динамика средней арифметической и реальной стоимости портфеля (в руб).

Таблица №2. Динамика средней арифметической и реальной стоимости портфеля (в руб).

Источник: Bloomberg, расчеты FinEx

Что такое подножка волатильности?

Разницу между средней арифметической и средней геометрической доходностью в академических кругах называют «volatility drag» или «подножка волатильности». Почему же речь идет о «подножке»? Потому что с точки зрения математики, чем более волатилен ряд доходностей, тем сильнее геометрическая доходность будет отставать от арифметической.

Volatility Drag = средняя арифметическая доходность — средняя геометрическая доходность

Несмотря на свою простоту, это формула позволяет сделать ряд интересных выводов — например, относительно опасности популярных у многих инвесторов инвестиций с использованием заемных средств («финансового рычага»). Когда инвестор рискует не только собственными средствами, но и занимает дополнительные деньги у своего брокера для того, чтобы увеличить размер своего портфеля, он увеличивает и его волатильность.

Например, использование рычага 2 (на каждый вложенный собственный рубль инвестиций инвестор получает в кредит еще один рубль и инвестирует его в рынок) обеспечивает удвоение арифметической доходности (без учета расходов в связи с использованием рычага). Но в случае падения, удваиваются и потери. В результате из-за бремени волатильности средняя геометрическая доходность меняется медленнее.

Как диверсификация отражается на волатильности портфеля?

Диверсификация портфеля сокращает volatility drag и поэтому положительно сказывается на доходности портфеля. Рассмотрим простой пример: инвестор может инвестировать в акции компании А или в акции компании А и Б. Волатильность акций компании А 26%, Б – 11%, их годовые доходности и результаты инвестирования для первого и второго случая представлены в таблице ниже. Как видно из таблицы, из-за большей волатильности первого инструмента, даже большие номинальные доходности несут в итоге результат хуже, чем в случае с инвестированием в разные инструменты даже пусть с меньшей общей доходностью. Это происходит как раз из-за того, что волатильность съедает большую доходность. Во втором случае портфель падает меньше чем при инвестировании исключительно в акции А, и даже небольшая доходность дает лучший итоговый результат в 6,7% за 10 лет.

График №2. Динамика портфеля только из акций компании А и портфеля из акций компаний А и Б в пропорции 50/50 (в руб).

Источник: Bloomberg, расчеты FinEx

Таблица №3. Динамика портфеля только из акций компании А и портфеля из акций компаний А и Б в пропорции 50/50 (в руб).

Источник

Как считать доходность

Считаем доходность финансовых инструментов и других вложений правильно

Основы

Доходность вложения за некоторый период — это отношение дохода ( I ) от вложения к его размеру ( C ) r = I / C .

По-другому её можно выразить как отношение прироста капитала к его размеру на начало периода r = C 0 C 1 − C 0 .

Отсюда получаем, что размер капитала на начало следующего периода будет равен C 1 = ( 1 + r ) C 0 = R C 0 , а на начало следующего C 2 = R C 1 = R 2 C 0 , и так далее C n = R n C 0 . Но только при условии, что доходность R не зависит от размера капитала (для реальных активов это не всегда так, о чём см. далее). Таким образом, «сложный процент» оказывается заключён уже в самом определении доходности.

То есть, если мы считаем доходность на разовое вложение C 0 , которое через n периодов (обычно в качестве периода берут год) даст капитал в размере C n , это будет R = n C n / C 0

= ( C 0 C n ) n 1 , или в процентах годовых r = n C n / C 0

− 1 , где n — количество лет (возможно, дробное).

Разумеется, из итогового капитала нужно вычитать все расходы, понесённые в связи с инвестицией.

Доходность с изъятиями и довнесениями

В предыдущем разделе мы посчитали доходность на разовое вложение. А что делать, если размер инвестированного капитала изменяется?

Так как доходность актива мы считаем постоянной, можно просто представить итоговый капитал в момент времени t как сумму независимых вложений D i , сделанных в моменты времени t i . Тогда каждое вложение будет приносить свою доходность t − t i периодов. А изъятие капитала мы просто представляем вложением со знаком минус. C t = R t − t 1 D 1 + R t − t 2 D 2 + …

Итоговый капитал тоже можно представить как изъятие в размере остатка, который ни секунды не приносил доходности: R t − t 1 D 1 + R t − t 2 D 2 + … + R 0 ( − C t ) = 0

Получили уравнение с одним неизвестным — R . Решив его, мы и получим искомую доходность. К сожалению, из-за множества слагаемых в высоких (и часто дробных) степенях, какой-либо формулы для его решения не существует.

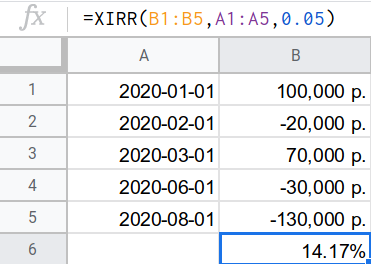
Поэтому его нужно решать численно (или подбором). Функция для решения такого рода уравнений обычно называется XIRR (в русском варианте экселя и родственников — ЧИСТВНДОХ — чистая внутренняя доходность) и принимает на вход даты, размеры вложений (включая изъятие остатка на последнюю дату), и начальное приближение доходности (численный метод не всегда может получить решение, если оно будет далеко от истинного значения, или просто «неудобным»; иногда нужно попробовать разные значения, чтобы получить результат). Выглядит это примерно так:

Как довложения при этом нужно учитывать только расходы, связанные с активом, которые вы несёте из своего кармана. А как изъятия, соответственно, только те суммы, которые вы получаете от него в свой карман.

То есть, если вы как вложения и изъятия учитываете только суммы перевода на брокерский счёт и обратно, то никакие движения денег внутри него учитывать уже не нужно. Если вы получаете дивиденды и купоны на отдельный счёт и используете их — надо учесть как изъятие. А если вам, например, пришлось доплатить налогов с другого счёта — не забудьте оформить их довложением, потому что это расход, связанный с инвестицией, хотя на него и не было ничего куплено.

Аналогично, если вы рассчитываете доходность сдаваемой в аренду квартиры. Все ваши налоги и прочие связанные с ней расходы надо считать как довложения в актив. А из конечной суммы изъятия не забывать вычесть налоги к уплате (или, более корректно, оформить их последним довложением с правильной датой после изъятия продажной стоимости).

Помимо этого, я бы оценивал примерную стоимость и считал за довложения в том числе и трудозатраты на управление активом.

Есть и приближённые способы вычисления доходности актива при наличии изъятий и довложений (например, по средневзвешенному задействованному капиталу), но, в эпоху электронных таблиц и библиотек финансовой математики, они более трудоёмкие, чем точный расчёт по XIRR, поэтому я не стану их описывать.

Взвешенная по времени доходность

Часто вам может быть интересно сравнить результаты своего портфеля с фондовым индексом, или каким-либо другим бенчмарком. Однако на ранних стадиях формирования портфеля, когда суммы довложений и изъятий составляют значительную его часть, время совершения операций может существенно влиять на результаты. Поэтому результат расчёта из предыдущего раздела, «взвешивающий» доходность по размеру задействованного капитала (поэтому называемый MWR, money-weighted return), для сравнения портфеля с индексом непригоден. Нужно сперва полученную доходность очистить от эффекта выбора времени операций (если, конечно, маркет-тайминг не является основой вашей стратегии). Полученная таким образом доходность называется взвешенной по времени (TWR, time-weighted return).

Чтобы её вычислить нужно разбить весь период инвестирования на отрезки, в которые внешних движений не происходило, перемножить доходности на каждом из отрезков, и возвести в степень, обратную продолжительности периода инвестирования (чтобы привести, например, к среднегодовой).

R = ( C 0 C 1 × C 1 ′ C 2 × C 2 ′ C 3 × ⋯ × C n − 1 ′ C n ) t 1 , здесь C n ′ — это капитал на конец n -го отрезка после учёта довложения/изъятия. Но не забывайте уменьшать C n на размер понесённых расходов, если они ещё не отражены в этом значении.

Характерная доходность

Все предыдущие методы для расчёта доходности учитывают только величины капитала на начало и конец периода инвестирования. Если у нас достаточно волатильный инструмент/портфель, то рассчитанная доходность может очень сильно зависеть не только от удачи в выборе моментов довложений/изъятий (которую устраняет расчёт доходности, взвешенной по времени), но и от выбора начальной и конечной точки. Чтобы устранить и этот шум, нужно рассчитывать доходность характерную.

Характерная доходность — это скорость роста капитала, очищенная от волатильности, медианная доходность по всем возможным интервалам внутри рассматриваемого периода. Чтобы её определить нам надо построить линию тренда на графике роста логарифма размера капитала (потому что нам важен относительный рост, а абсолютный).

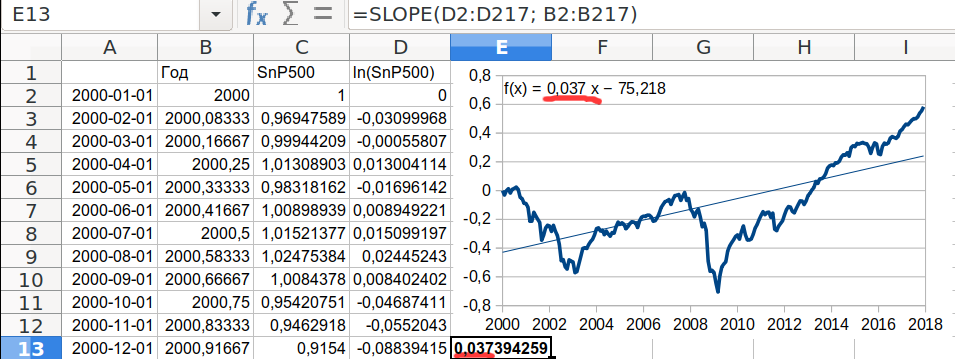
Это можно сделать в электронной таблице (функция «вставить линию тренда» и показать формулу зависимости на графике есть практически везде), или выполнить приближение соответствующей линейной модели другим удобным вам способом (в том же экселе нужный результат даст функция SLOPE/НАКЛОН). Работая в экселе не забывайте, что по оси x графика должен быть отложен именно год числом, а не дата. Иначе вы получите не годовую доходность, а дневную (хотя пересчитать её в годовую тривиально).

В примере ниже показано, что характерная реальная доходность индекса SnP500 с 2000 по 2018 составила 3,7%г.

Номинальная и реальная доходность

Используя в расчётах те суммы довложений/изъятий, которые вы фактически сделали и те размеры капитала, которые фактически зафиксировали, вы будете получать номинальные доходности. Однако, в ситуациях с высокой/неравномерной инфляцией (США сюда тоже относятся) эти доходности совершенно неинформативны.

Чтобы получить реальную доходность, необходимо все суммы, участвующие в расчётах, скорректировать на инфляцию, разделив на значение соответствующего индекса на дату вложения/изъятия/фиксации. Дата начала и направление отсчёта индекса и его величина значения при этом не имеют.

В качестве индекса традиционно используется индекс потребительских цен, но можно использовать и другие: однодневных межбанковских кредитов, доходности гособлигаций, дефлятор ВВП, цен производителей и т.д. в зависимости от целей расчёта доходности. Т.е. реальная доходность не однозначна и требует указания на индекс, с помощью которого она рассчитывалась. По умолчанию предполагается, что использован индекс потребительских цен страны происхождения инструмента, что не всегда удобно (например, хотя характерная реальная доходность индекса SnP500 по ИПЦ США в предыдущем примере была 3,7%г, по ИПЦ РФ она будет отрицательной, примерно −1%г).

Реальные активы

У реальных активов, в отличие от идеальных, доходность зависит от объёма вложенного капитала, причём иногда довольно сложным образом. Рассмотрим основные составляющие этой зависимости.

Нижний барьер капитализации. «Довложение» суммы меньшей этого барьера не приведёт к росту дохода (т.е. доходность на вложенный капитал упадёт). Барьер возникает из-за того, что существует неделимая единица актива, и суммы меньшие стоимости этой единицы будут простаивать.
Верхний барьер капитализации. Рост задействованного капитала сверх барьера не ведёт к росту дохода, доходность на капитал падает. Эффект связан с тем, что любая доходность, в конечно итоге, происходит от создания и продажи экономических благ. Если ресурсы/мощности/рынок сбыта задействованы полностью, то вливание нового капитала роста дохода уже не принесёт.
Убывающая отдача. Возникает с приближением к верхнему барьеру капитализации (или какому-то из промежуточных): получение каждой следующей единицы дохода начинает стоить всё бо́льших вложений. Также может быть следствием конкуренции множества агентов за фиксированный доход, который распределяется пропорционально вложенным средствам. Так работают финансовые рынки: размер прибыли которую могут распределить компании, и размер процентов, которые они готовы заплатить по долгам, на коротких горизонтах фиксированы, поэтому при резком росте вложенного в них капитала, доходность каждой последующей единицы падает.
Экономия на масштабе. В основном характерна для производственных активов, где велика доля фиксированных издержек, и при росте выпуска каждая последующая единица несёт себе меньшую их долю т.е. обходится дешевле. Однако может возникать и как следствие преодоления нижнего барьера капитализации: если стоимость единицы актива, скажем, 200Кр, то каждые последующие 200Кр капитала приводят к тому, что сокращается время простоя полученного дохода до следующей покупки актива, а, следовательно, растёт эффективная доходность.

Манипуляции доходностью

В интернете находится огромное количество способов извлечения огромной доходности из достаточно простой инвестиционной деятельности. Я здесь имею в виду не мошенников, которые предлагают отдать им деньги в обмен на обещания этой высокой доходности, а именно самостоятельную работу. Как правило, практически все они показывают привлекательные цифры за счёт ошибок в расчёте доходности (и игнорирования операционных рисков, но это тема для другой статьи).

В расходы на инвестицию учитываются только стоимость самого объекта инвестирования, но не сопутствующие затраты, которые могут быть сопоставимы или даже больше. Особенно любят забывать стоимость проведения сделок, текущие платежи (например, коммунальные) и налоги. Никто в принципе не учитывает стоимость трудозатрат.
Игнорируются барьеры капитализации и убывающая отдача. Вы можете, условно, сдавать гараж стоимостью 200Кр за 2Кр/мес, имея по итогам года после всех расходов 20Кр или 10%, но пока вы 10 лет копите на следующий, эти деньги должны где-то лежать под меньшую доходность. А после десятого гаража вы уже хотите нанять управляющего, только никто не соглашается работать за 16Кр/мес, которые этот десяток гаражей приносит.
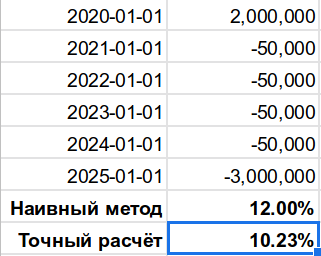
Используется «наивный» расчёт [суммарный доход]/[суммарный расход]/[количество лет], без учёта сложных процентов и временно́й стоимости денег. Как показано на рисунке ниже, даже для небольшого промежутка времени разница такого метода с точным может быть достаточно велика, чтобы склонить к ошибочному решению.

Не ведитесь на манипуляции, считайте доходность правильно.

Здесь я выкладываю лишь собственные размышления/исследования/расчёты, иногда собственное же изложение чужих мнений или результатов исследований. Размещённая информация может содержать ошибки, быть неактуальной на момент прочтения, допускать множество интерпретаций и проч. Я не занимаюсь образовательной деятельностью и не даю инвестиционных рекомендаций ни на этом сайте, ни в частном порядке.

Может быть, вам показалось, но способов получить гарантированную доходность за счёт каких бы то ни было финансовых инструментов, портфелей или торговых стратегий НЕ СУЩЕСТВУЕТ. Хуже того, способов гарантированно сохранить свой капитал тоже НЕ СУЩЕСТВУЕТ.

Источник