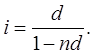Эквивалентность процентных и учетных ставок
Определение эквивалентной ставки.
Финансовые операции (ставки) называются эквивалентными, если они дают один и тот же результат.
Вычисление простой учетной ставки, которая эквивалентна заданной простой процентной ставке:
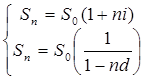
Пример 3.1. Необходимо определить значение простой учетной ставки, эквивалентной простой ставке процентов, равной 10%, если n=10.
3,2,Вычисление простой процентной ставки,
эквивалентной простой учетной ставке:
Пример 3.2. Какова доходность, измеренная в виде ставки простых процентов (K=365 дней), учета векселя по учетной ставке 10% ( 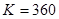
3.3.Эквивалентность простых ставок при разных временных базах K=365 для простых процентов, 

Пример 3.3. Операция учета должна принести 30% дохода (в расчете на год). Срок ссуды 55 дней. K=365 для простых процентов. Найти эквивалентную простую учетную ставку (K=360).
3.4.Вычисление простой процентной ставки, эквивалентной заданной сложной процентной ставке:

Пример 3.4. Ссуда выдана под 20 сложных годовых процентов. Каков должен быть уровень простой процентной ставки при сроке: а) 10 лет, б) 8 месяцев?
Ответ: 51,92%; 19,39%.
3.5.Вычисление сложной процентной ставки, эквивалентной простой процентной ставке:
Пример 3.5. Какой годовой ставкой сложных процентов можно заменить в контракте простую ставку в 18%, не изменяя финансовых отношений сторон? Срок операции 580 дней.
3.6.Вычисление сложной процентной ставки, эквивалентной простой учетной ставке.

Пример 3.6. Какова эффективность, выраженная в годовой сложной процентной ставке, дисконтирования векселя по простой учетной ставке 8%? Срок оплаты векселя наступит через 120 дней. (Временные базы по умолчанию).
3.7.Вычисление номинальной процентной ставки, эквивалентной заданной эффективной процентной ставке:

Пример 3.7. При разработке соглашения стороны договорились о том, что действительная доходность финансовой операции должна составить 9%, причем начисление процентов будет осуществляться помесячно. Найти номинальную ставку процентов.
3.8+.Вычисление годовой сложной процентной ставки, эквивалентной заданной непрерывной ставке процентов:
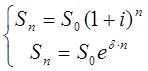
Пример 3.8. Множитель наращения при дискретно изменяющихся непрерывных процентах составил 2,5345 при n=10 лет. Найти эквивалентную годовую ставку сложных процентов.
3.9. Вычисление средних простых процентных ставок:
Пример 3.9. В контракте предусматривается начислять простые проценты в следующих размерах
| Период |  | 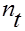 (в годах) (в годах) |  |
| 0,10 | 0,5 | 0,05 | |
| 0,12 | 1,0 | 0,12 | |
| 0,15 | 0,5 | 0,075 | |
| 2,0 | 0,245 |
Найти эквивалентную среднюю простую процентную ставку и наращенную сумму, если S0=10 тыс. руб.
Ответ: 12,25%; 12,45 тыс.руб.
3.10. Вычисление сложных средних процентных ставок:
Пример 3.10. Процентная ставка по ссуде определена на уровне 8,5% плюс маржа 0,5% в первые два года, 0,75% в следующие три года. Найти среднюю ставку.
3.11. Финансовая эквивалентность обязательств.
Определение. Финансовые изменения называются эквивалентными, если после изменений условий, платежи, приведенные к одному моменту времени, окажутся равными.
Пример 3.11. Имеются два обязательства. Условие первого: 



Ответ: 387,10 тыс.руб.; 390,70 тыс. руб.; неэквивалентны.
3.12. Консолидирование задолженностей при простой процентной ставке.
Определение. Консолидирование задолженностей означает приведение этих задолженностей к одному моменту времени.
Пример 3.12. Решено консолидировать 3 платежа со сроками 15.05, 15.06, 15.08, суммы платежей 10 тыс. руб., 20 тыс. руб., 15 тыс. руб. Ставка простых процентов равна 8%. Найти консолидированную сумму к 01.08.
3.13.Консолидирование платежей при простой учетной ставке.
Пример 3.13. Два векселя со сроками 10.06 на 10 тыс. руб. и 01.08 на 20 тыс. руб. заменяются одним с продлением срока до 01.10. При объединении векселей применена простая учетная ставка 8%. Сроки пролонгации составят 113 и 61 день.


Последнее изменение этой страницы: 2017-03-14; Просмотров: 3782; Нарушение авторского права страницы
Источник
Занятие 2. Простые учетные ставки
Учетная ставка рассчитывается отношением наращения (F-P) к ожидаемой в будущем к получению, или наращенной, величине F.
Схемапростых процентов предполагает неизменность базы,с которойпроисходит начисление.
Банковское (коммерческое) дисконтирование применяется в ситуации предварительного начисления простого процента, например, при операции по учету векселя, заключающейся в покупке банком векселя у владельца до наступления срока оплаты по цене, меньшей той суммы, которая должна быть выплачена по векселю на дату его погашения. Сумма, которую получает векселедержатель при досрочном учете векселя, называется дисконтированной величиной векселя.
Банковское дисконтирование нельзя осуществить во всех ситуациях, например, по достаточно большой учетной ставке и задолго до срока платежа.
Возможно финансовое соглашение, предусматривающее изменение во времени учетной ставки.
При применении наращения по простой учетной ставке величина начисляемых процентов с каждым годом увеличивается. Простая учетная ставка обеспечивает более быстрый рост капитала, чем такая же по величине процентная ставка.
Цель проведения занятия— научиться проводить расчеты по схеме простых учетных процентов, используя формулы финансовых вычислений.
Основные формулы








P- вложенная сумма (сумма, которую получает владелец векселя при его учете) ;
F – наращенная сумма (номинальная стоимость векселя);
n- количество периодов продолжительности финансовой операции;
t —продолжительность финансовой операции в днях;
T- количество дней в году;
Типовые задачи с решениями
Задача 1.В банк 6 мая предъявлен для учета вексель, на сумму 140 тыс. руб. со сроком погашения 10 июля того же года. Банк учитывает вексель по учетной ставке 40% годовых, считая, что в году 365 дней. Определить сумму, получаемую векселедержателем от банка, и комиссионные, удерживаемые банком за свою услугу. За какое время до срока платежа операция учета векселя имеет смысл?
Решение
По формуле (2.1) при F = 140.; n = 65/365, d = 0,4 получим:
Р = 140×(1-0,4 ×65/365)=129, 89
Векселедержатель получит от банка 129,89 тыс. руб.
Комиссионные банка ( или дисконт) определяются по формуле D= F — P
D= F — P= 140-129, 89=10, 11 тыс. руб.
Комиссионные, удерживаемые банком за свою услугу, равны 10,11 тыс. руб.
Учет векселя по учетной ставке имеет смысл при n 2,5 года сумма Р, которую должен получить владелец векселя при его учете, становится отрицательной.
Задача 2.Кредит в размере 400 тыс. руб. выдан по простой учетной ставке 25% годовых. Определить срок кредита, если заемщик планирует получить на руки 350 тыс. руб.
Решение
По формуле (2.7. ) при F =400 ; Р=350; d=0,25 получаем:
Срок кредита равен 0,5 года.
Задача 3.Вексель на сумму 900 тыс. руб. учитывается по простой учетной ставке за 120 дней до погашения с дисконтом 60 тыс. руб. в пользу банка. Определить величину годовой учетной ставки при временной базе 360 дней в году.
Решение.
По формуле (2.6) при F=900; F-P=60; t=120; T=360 дней, получим :
Годовая учетная ставка при временной базе 360 дней в году равна 20% годовых.
Задача 4.В банк предъявлен вексель на сумму 500 тыс. руб. за полтора года до его погашения. Банк согласен учесть вексель по переменной простой учетной ставке, установленной следующим образом: первые полгода – 30% годовых, следующие полгода- 36% годовых, затем каждый квартал ставка повышается на 2%. Определите дисконт банка и сумму, которую получит векселедержатель.
Решение.
По формуле (2.8) вычислим множитель наращения:
1- ( 0,5 × 0,30 +0,5 × 0,36 + 0,25 × 0,38 + 0,25 × 0,4) = 0, 475
Р = 500 × 0,475 = 237,50
Сумма, полученная владельцем векселя равна 237 500 руб.
По формуле 1.11 дисконт равен D = 500- 237,5 = 262,5
Дисконт банка равен 262 500 руб.
Задача 5.Банк 1 января учел два векселя со сроками погашения 6 февраля и 14 марта того же года. Применяя учетную ставку 10% годовых, банк удержал комиссионные в размере 1000 руб. Определить номинальную стоимость векселей, если номинальная стоимость второго векселя в 2 раза больше, чем номинальная стоимость первого векселя.
Решение
Обозначим номинальную стоимость первого векселя через F, тогда номинальная стоимость второго векселя составит 2∙F.
По таблице порядковых дней в году определим, что первый вексель учтен за 36 дней до срока погашения, а второй вексель учтен за 72 дней до срока погашения.
По формуле (2.5) величина дисконта для первого векселя равна
По формуле (2.5 ) величина дисконта для второго векселя равна
Учитывая, что комиссионные банка за учет двух векселей составили 1000 руб., запишем:
Номинальная стоимость первого векселя составит 20 тыс. руб., номинальная стоимость второго векселя составит 40 тыс. руб.
Источник