Найти распределение инвестиций между предприятиями

29.2.3. Распределение инвестиций для эффективного использования потенциала предприятия

Совет директоров фирмы рассматривает предложения по наращиванию производственных мощностей для увеличения выпуска однородной продукции на четырех предприятиях, при­надлежащих фирме.

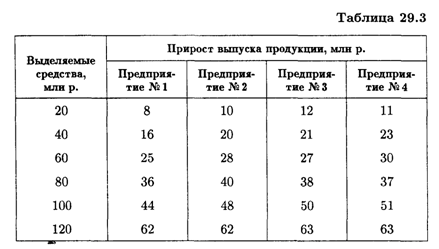
Для расширения производства совет директоров выделя­ет средства в объеме 120 млн р. с дискретностью 20 млн р. Прирост выпуска продукции на предприятиях зависит от вы­деленной суммы, его значения представлены предприятиями и содержатся в табл. 29.3.

Найти распределение средств между предприятиями, обес­печивающее максимальный прирост выпуска продукции, при­чем на одно предприятие можно осуществить не более одной инвестиции.

Решение. Разобьем решение задачи на четыре этапа по количеству предприятий, на которых предполагается осущест­вить инвестиции.

Рекуррентные соотношения будут иметь вид:

Для предприятия № 1

Для всех остальных предприятий

Решение будем проводить согласно рекуррентным соотно­шениям в четыре этапа.

1-й этап. Инвестиции производим только первому пред­приятию. Тогда

2-й этап. Инвестиции выделяем первому и второму пред­приятиям. Рекуррентное соотношение для 2-го этапа имеет вид

При Х = 20 F2(20) = max (8 + 0,0 + 10) = max (8, 10) = 10,

При X = 40 F2(40) = max (16,8 + 10,20) = max (16, 18, 20) =20,

При Х = 60 F2(60) = max (25,16 + 10, 8 + 20,28) = max (25,26, 28,28) =28,

При Х = 80 F2(80) = max (36,25 + 10,16 + 20,8 + 28,40) = max (36, 35, 36, 36, 40) = 40,

При Х = 100 F2(100) = max (44,36 + 10,25 + 20,16 + 28,8 + 40,48) = max (44, 46, 45, 44, 48, 48) = 48,

При Х = 120 F2(120) = max (62,44 + 10,36 +20,25 + 28,16 + 40,8 + 48,62) = max (62, 54, 56, 53, 56, 56, 62) = 62.

3-й этап. Финансируем 2-й этап и третье предприятие. Расчеты проводим по формуле

При Х = 20 F3(20) = mах (10, 12) = 12,

При X = 40 F3(40) = max (20,10 + 12,21) = max (20, 22, 21) = 22,

При Х = 60 F3(60) = max (28,20 + 12,10 + 21,27) = max (28, 32, 31, 27) = 32,

При Х = 80 F3(80) = max (40,28 + 12,20 + 21,10 + 27,38) = max (40, 40, 41, 37, 38) = 41,

При X = 100 F3(100) = max (48,40 + 12,28 + 21,20 + 27,10 + 38,50) = max (48, 52, 49, 47, 48, 50) = 52,

При Х = 120 F3(120) = max (62,48 + 12,40 + 21,28 + 27,20 + 38,10 + 50,63) = max (62, 60, 61, 55, 58, 60, 63) = 63.

4-й этап. Инвестиции в объеме 120 млн р. распределяем между 3-м этапом и четвертым предприятием.

При Х = 120 F4(120) = max (63,52 + 11,41 + 23,32 + 30,22 + 37,12 + 51,63) = max (63, 63, 64, 62, 59, 63, 63) = 64.

Получены условия управления от 1-го до 4-го этапа. Вер­немся от 4-го к 1-му этапу. Максимальный прирост выпус­ка продукции в 64 млн р. получен на 4-м этапе как 41 + 23, т. е. 23 млн р. соответствуют выделению 40 млн р. четвертому предприятию (см. табл. 29.3). Согласно 3-му этапу 41 млн р. получен как 20 + 21, т. е. 21 млн р. соответствует выделеник 40 млн р. третьему предприятию. Согласно 2-этапу 20 млн р. получено при выделении 40 млн р. второму предприятию.

Таким образом, инвестиции в объеме 120 млн р. целесообразно выделить второму, третьему и четвертому предприятиям по 40 млн р. каждому, при этом прирост продукции будет максимальным и составит 64 млн р.

Источник

Распределение инвестиций для эффективного использования потенциала предприятия

Достаточно простая задача из цикла дисциплин «Методы принятия оптимальных решений» или «Исследование операций». В разных ВУЗ’ах это может называться по-разному, но суть от этого не меняется. Давайте разберёмся с данными задачами без длинных и непонятных формул на практическом примере.

Условие задания

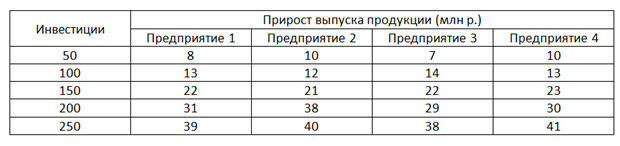
Всегда представляется в виде таблицы, наподобие продемонстрированной ниже.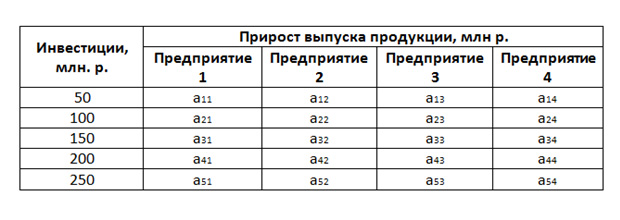

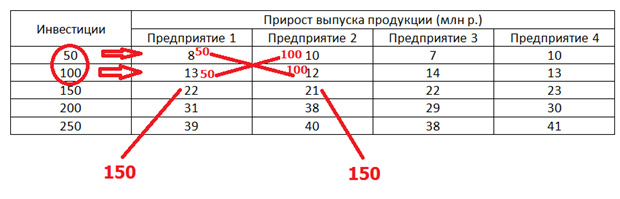
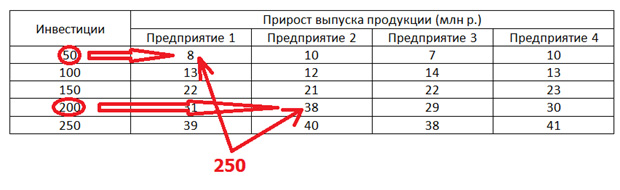
В первом столбце показаны различные варианты объёмов инвестиций, которые нужно распределить между «энным» количеством предприятий. В данном случае у нас четыре предприятия. Со второго по пятый столбец клетки заполняются данными об отдаче, то есть, какой прирост продукции нами будет получен при том или ином инвестировании.

Естественно, условие будет требовать наиболее выгодного распределения, то есть, как нам распределить 250 млн. р., чтобы отдача была на максимум.

Например, мы можем вложить по 50 миллионов в три завода, а четвёртому предприятию дать 100 миллионов инвестиций. Возможно, выгоднее будет дать 200 миллионов третьему заводу, а первому 50 и тем самым достичь максимальной отдачи. То есть, с первого взгляда непонятно, сколько денег и куда направить. Путём перебора всех возможных вариантов, мы это выясним.

Алгоритм решения

В учебниках эти задачи решаются долго и в четыре этапа, два из которых полностью дублируют действия предыдущих шагов и теряют наше время. Мы всё решим в два шага, и будем надеяться, принцип вы усвоите. Есть следующие условия.

Первый этап

Сначала мы проверим, какую отдачу можно получить, распределяя инвестиции только между первым и вторым предприятием.

f2(50) = max (8; 10) = 10

f2(100) = max (13; 12; 8+10) = 18

Вторая запись означает, что мы можем отдать 100 миллионов либо первому, либо второму предприятию, а можем дать по пятьдесят и тому, и другому.

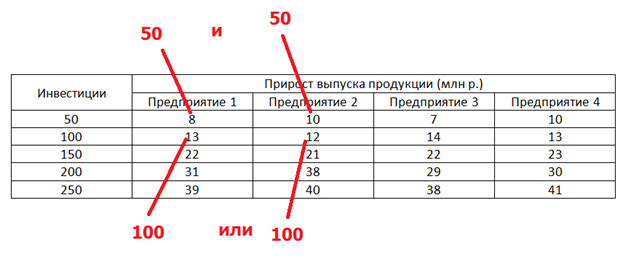
Распределяю наши средства, мы получаем большую отдачу, чем отдавая всё кому-то одному. Идём далее.

f2(150) = max (22; 21; 8+12; 13+10) = 18

Смысл тот же самый. Всё одному или разбиваем по разным направлениям.

f2(200) = max (31; 38; 21+10; 21+8) = 38

Тут уже выгоднее отдать 200 миллионов лишь второму цеху. Дробить бессмысленно.

f2(250) = max (39; 40; 13+21; 22+12; 8+38; 31+10) = 46

А здесь выгодно дать 200 млн второму предприятию и ещё 50 – первому.

Из всех наших вычислений следует, что самым выгодным вариантом при инвестировании только в первые два завода является последняя альтернатива. Так наша отдача достигает максимума.

Второй этап

Посчитаем, каковы максимальные выгоды от инвестиций в третье и четвертое предприятие. С тем, как строятся вычисления, вы разобрались, поэтому можете сверяться с тем, что описано ниже.

f3(50) = max (7; 10) = 10

f3(100) = max (14; 13; 7+10) = 17

f3(150) = max (22; 23; 14+10; 7+13) = 24

f3(200) = max (29; 30; 7+23; 22+10; 14+13) = 32

f3(250) = max (38; 41; 22+13; 14+23; 7+30; 29+10) = 39

Итак, выгодны 200 млн для третьего завода и 50 для четвертого.

Теперь сравним, что будет, если мы дадим инвестиции 4-ому предприятию или разделим их в соответствие с предыдущими «шагами» — нашими посчитанными f.

f3(250) = max (41; 13+24; 23+17; 10+32; 7+30; 29+10) = 42.

Выводы

Наиболее благоприятный исход для инвестора – это выделить 50 млн для 1-ого предприятия и 200 млн для 2-ого.

Источник

Градиент 11782

Решить задачу о распределении инвестиций между предприятиями П₁, П₂, П_3. Инвестируется сумма 6 усл. ден. ед. Сопоставить полученные оптимальные решения с решениями, предписывающими выделение всего объема инвестиций только одному из предприятий, либо распределение инвестиций поровну между всеми предприятиями, и вычислить сколько процентов прибыли теряется в каждом из этих случаев.

Ожидаема прибыль предприятий

I этап. Условная оптимизация.

Предположим, что все средства в количестве x₃ = 6 отданы предприятию №3. В этом случае, максимальный доход, как это видно из таблицы, составит f₃(u₃) = 69, следовательно, F₃(e₃) = f₃(u₃)

Определяем оптимальную стратегию при распределении денежных средств между предприятиями №2, 3. При этом рекуррентное соотношение Беллмана имеет вид: F₂(e₂) = max(x₂ ≤ e₂)(f₂(u₂) + F₃(e₂-u₂))

Определяем оптимальную стратегию при распределении денежных средств между предприятиями №1, 2, 3. При этом рекуррентное соотношение Беллмана имеет вид: F₁(e₁) = max(x₁ ≤ e₁)(f₁(u₁) + F₂(e₁-u₁))

Поясним построение таблиц и последовательность проведения расчетов.

Этап II. Безусловная оптимизация.

Из таблицы 3-го шага имеем F*₁(e 0 = 6) = 70. То есть максимальный доход всей системы при количестве средств e 0 = 6 равен 70

Из этой же таблицы получаем, что 1-му предприятию следует выделить u*₁(e 0 = 6) = 2, При этом остаток средств составит:

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

Постановка и решение задачи оптимального распределения инвестиций

Экономическая эффективность капитальных вложений (инвестиций) — одна из важнейших проблем планирования, характеризующая целесообразность вложений финансовых и других средств.

Рационального распределения инвестиций можно достигнуть лишь на основе тщательных экономических расчетов, дающих возможность определить пути достижения максимальной отдачи, т.е.

При установлении структуры инвестиций на государственном уровне необходимо исходить из предусмотренных темпов развития отраслей экономики страны, обеспеченности их основными фондами и степени использования мощностей, объема сырья и материалов, поступающих из смежных отраслей, и ряда других факторов.

Межотраслевое распределение инвестиций должно сопровождаться распределением вложений внутри отрасли и, в частности, между предприятиями, выпускающими однородную продукцию. Критерием для оптимального распределения инвестиций могут служить максимальная прибыль, максимальный суммарный прирост продукции, максимальное снижение себестоимости, максимальная занятость населения и т.п.

Задача оптимального распределения инвестиций по своей природе комбинаторная. Например, при определении фондоотдачи от 10 млрд руб. в четыре отрасли промышленности необходимо перебрать все распределения числа 10 на четыре группы. При условии распределения только из целых чисел необходимо подсчитать 286 комбинаций:

(10, 0, 0, 0); (9, 1, 0, 0); (9, 0, 1, 0); (9, 0, 0, 1) . ;

(8, 1, 1, 0); (8, 1, 0, 1); (8, 0, 1, 1); (8, 2, 0, 0); (8, 0, 2, 0); (8, 0, 0, 2);

(4, 3, 2, 1); . (4, 2, 2, 2); .

Если требуется дополнительно определить оптимальное решение задачи в случае, когда инвестиции в целом составляют 9, 8, 7, . 1 млрд руб., то необходимо провести большой объем вычислительной работы.

Метод динамического программирования позволяет находить оптимальное решение задач по распределению однородных средств между объектами при значительно меньшем, по сравнению с комбинаторным способом решения, объеме вычислительной работы.

В общем виде математическая постановка задач по распределению однородных средств (капитальных вложений, машин, сырья и т.д.) между объектами формулируется следующим образом: найти значения неизвестных xv х2, . х, . хп, т.е. план распределения, удовлетворяющий условиям:

обращающие в максимум функцию

(4.2)

где— сумма возможных вложений по j-му объекту (отрасль, предприятие, цех, участок);

— фондоотдача по предполагаемому j-му объекту, т.е. функция отдачи капитальных вложений (прибыль, прирост продукции и т.д.).

Алгоритм, предложенный Беллманом, справедлив для функцийлюбого вида и является одним из простейших примеров применения динамического программирования. Идея алгоритма состоит в том, что последовательно решаются задачи оптимального распределения средств между первыми j объектами (здесь j принимает значения 1, 2, 3, . n). Последняя из этих задач является решением поставленной.

В задаче по распределению средств между объектами всегда предполагаются известными значения функций f.(x) при всех возможных значениях аргументов (табл. 4.7).

Источник

Задача распределения ресурсов

Пример №1 . Планируется работа двух предприятий на n лет. Начальные ресурсы равны s0. Средства x, вложенные в 1-е предприятие в начале года, дают в конце года прибыль f1(x), и возвращаются в размере g1(x). Средства y, вложенные в 2-е предприятие в начале года, дают в конце года прибыль f2(y) и возвращаются в размере g2(y). В конце года возвращенные средства заново перераспределяются между отраслями. Определить оптимальный план распределения средств и найти максимальную прибыль.

Задачу решим методом динамического программирования. Операцию управления производственным процессом разобьём на этапы. На каждом из них управление выберем так, чтобы оно приводило к выигрышу как на данном этапе, так и на всех последующих до конца операции. В этом состоит принцип оптимальности, сформулированный американским математиком А. Беллманом.
Разобьём весь период на три этапа по годам и будем нумеровать их, начиная с первого.
Обозначим через x_k и y_k количество средств выделяемых каждому предприятию на k-ом этапе, а через x_k + y_k = a_k – общее количество средств на этом этапе. Тогда первое предприятие приносит на этом этапе 3 x_k, а второе 4 y_k единиц дохода. Общий доход на k-ом этапе 3x_k + 4y_k.
Обозначим через f_k (a_k) – максимальный доход, который получает отрасль от обоих предприятий на k-ом и всех последующих. Тогда функциональное уравнение, отражающее принцип оптимальности Беллмана, принимает вид:
f_k (a_k)=max<3x_k + 4y_k + f_k+1 (a_k+1)>. (1)
Так как x_k + y_k = a_k, то y_k = a_k — x_k и 3x_k + 4y_k = 3x_k + 4(a_k — x_k) = — x_k + 4a_k. Поэтому f_k(a_k) = max<-x_k + 4a_k + f_k+1(_ak+1)>. (2)
0 ≤ x_k ≤ a_k
Кроме того, ak – это средства выделяемые обои предприятиям на k-ом этапе, и они определяются остатком средств, получаемых на предыдущем (k-1)-ом этапе. Поэтому по условию задачи оптимальное управление на каждом этапе
a_k = 0,5x_k-1 + 0,2y_k-1 = 0,5x_k-1+0,2(a_k-1 — x_k-1) = 0,3x_k-1+0,2a_k-1. (3)

I.Условия оптимизации
Планирование начинаем с последнего третьего этапа

Источник