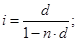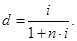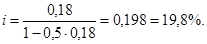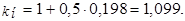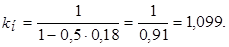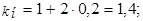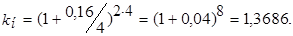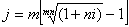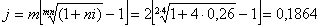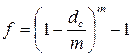Эквивалентные процентные ставки
Для нахождения эквивалентных процентных ставок используют уравнения эквивалентности.
P (1 + ni) = P/ (1 — nd) или (1 + ni) = 1 / (1 — nd),
т.е. необходимо приравнять соответствующие коэффициенты наращения.
Отсюда d = i / (1 + ni) и i = d / (1 — nd).
Срок уплаты по долговому обязательству — полгода, простая учетная ставка — 18%. Какова доходность данной операции, измеренная в виде простой ставки ссудных процентов?
i = 0.18 / (1 — 0.5 х 0.18) = 0.198 = 19.8%.
Для нахождения эквивалентности между собой годовой сложной ссудной ставки и годовой сложной номинальной ссудной ставки приравняем выражения: S = P (1 + Іс)п и S = P (1 + j/m)mn, т.е. (1 + Іс)п = (1 + j/m)mn.
Отсюда Іс = (1 + j/m) m — 1.
Полученная годовая ставка сложных процентов, эквивалентная номинальной процентной ставке, называется эффективной ставкой сложных процентов. Ее необходимо знать для определения реальной доходности или сравнения процентов, когда используются разные интервалы начисления.
Рассчитать эффективную ставку сложных процентов, если номинальная ставка 24% и начисление процентов ежемесячное.
іс = (1 + 0.24 / 12)12 — 1 = 0.268 = 26.8%.
Определить, под какую ставку процентов выгоднее поместить капитал в 10 000 тыс.
а) под простую ссудную ставку 20% годовых;
б) под сложную ссудную ставку 12% годовых при ежеквартальном начислении процентов.
Здесь не обязательно считать величину наращенной суммы при различных ставках. Поэтому не важна величина первоначального капитала. Достаточно, например, найти простую процентную ставку, эквивалентную данной сложной ставке, т.е. использовать формулу
і = [(1 + j / m)mn — 1] / n = [(1 + 0.12 / 4)20 — 1] / 5 = 0.1612 = 16.12%.
Поскольку простая процентная ставка 16.12%, которая дала бы одинаковый с данной сложной процентной ставкой (12%) результат, значительно ниже предложенной в первом варианте ставки (20%), ясно, что гораздо выгоднее первый вариант вложения (под простую ставку 20% годовых).
Посчитаем теперь наращенные суммы в обоих случаях:
а) S = 10 000 (1 + 5 х 0.2) = 20 000 тыс. р.;
б) S = 10 000 (1 + 0.12 / 4)20 = 18 061 тыс. р.
Полученный результат подтверждает ранее сделанный вывод о том, что первый вариант более выгоден, поскольку дает большую сумму наращения. При этом использование эквивалентных ставок вдвое сокращает расчеты.
Вексель учтен за три месяца до срока его погашения по учетной ставке 20% годовых. Определить значение эквивалентной ставки простых процентов, определяющей доходность операции учета.
Простая ставка процентов равна 20% годовых. Определить значение эквивалентной ей учетной ставки при выдаче ссуды на полгода.
Кредит на два года предоставлен по ставке сложных процентов 16% годовых. Определить значение эквивалентной учетной ставки при выдаче ссуды на полгода.
По депозитному сертификату сроком на пять лет начисляются простые ссудные проценты по ставке 15% годовых. Определить эквивалентную ставку сложных процентов.
Банк ежемесячно начисляет проценты на вклады по номинальной годовой ставке 12% годовых. Определить доходность вкладов по сложной годовой ставке процентов.
Можно сделать следующие выводы:
Значение эффективной ставки больше значения номинальной, а совпадают они при m = 1.
Простая учетная ставка всегда меньше эквивалентных ей других ставок (поскольку наращение по этой ставке при прочих равных условиях всегда быстрее).
Эквивалентность различных процентных ставок не зависит от величины первоначальной суммы Р (первоначальная сумма предполагается одинаковой).
Эквивалентность процентных ставок всегда зависит от продолжительности периода начисления процентов за исключением случаев эквивалентности между собой сложных процентных ставок разного вида (если период начисления один и тот же).
Источник
Решение. Эквивалентность процентных ставок различного типа
Эквивалентность процентных ставок различного типа
Эквивалентные процентные ставки – это такие процентные ставки разного вида, применение которых при одинаковых начальных условиях дает одинаковые результаты.
Приравнивая попарно формулы для определения наращенной суммы, можно получить соотношения, выражающие зависимость между любыми двумя различными процентными ставками.
Приравнивая соотношения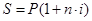 
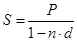
и 
, получим:
– простая годовая ставка ссудного процента 
– простая годовая учётная ставка 
Пример 11.Срок уплаты по долговому обязательству – полгода, учетная ставка равна 18%. Какова доходность данной операции, измеренная в виде простой ставки ссудного процента?
Используем формулу простой годовой ставки ссудного процента
Проверка: 1. При простой процентной ставке 
2. При простой учётной ставке 
Пример 12.Определить, под какую ставку процентов выгоднее поместить капитал на два года:
а) под простую ставку процентов 20% годовых;
б) под сложную ставку в 16% при ежеквартальном начислении?
Решение
I способ. Найдём простую процентную ставку, эквивалентную данной сложной ставке, воспользовавшись формулой :
. 
, т.е. 18,43%.
Так как простая процентная ставка (20%), которая дала бы одинаковый с данной сложной процентной ставкой результат, превышает предложенную (18,43%), ясно, что выгоднее использовать простую процентную ставку.
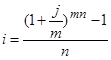
II способ.Посчитаем коэффициенты наращения, получаемые в обоих случаях: а) под простую ставку процентов 
б) под сложную ставку при ежеквартальном начислении
Разница в результатах подтверждает сделанный ранее вывод.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Эквивалентность процентных ставок
Достаточно часто в практике возникает ситуация, когда необходимо произвести между собой сравнение по выгодности условий различных финансовых операций и коммерческих сделок. Условия финансово-коммерческих операций могут быть весьма разнообразными и напрямую несопоставимыми. Для сопоставления альтернативных вариантов ставки, используемые в условиях контрактов, приводят к единообразному показателю.
Различные финансовые схемы можно считать эквивалентными в том случае, если они приводят к одному и тому же финансовому результату.
Эквивалентная процентная ставка – это ставка, которая для рассматриваемой финансовой операции даст точно такой же денежный результат (наращенную сумму), что и применяемая в этой операции ставка.
Классическим примером эквивалентности являются номинальная и эффективная ставка процентов:
Эффективная ставка измеряет тот относительный доход, который может быть получен в целом за год, т.е. совершенно безразлично – применять ли ставку j при начислении процентов m раз в год или годовую ставку i, – и та, и другая ставки эквивалентны в финансовом отношении.
Поэтому совершенно не имеет значения, какую из приведенных ставок указывать в финансовых условиях, поскольку использование их дает одну и ту же наращенную сумму. В США в практических расчетах применяют номинальную ставку, а в европейских странах предпочитают эффективную ставку процентов.
Если две номинальные ставки определяют одну и ту же эффективную ставку процентов, то они называются эквивалентными.
Пример 1. Каковы будут эквивалентные номинальные процентные ставки с полугодовым начислением процентов и ежемесячным начислением процентов, если соответствующая им эффективная ставка должна быть равна 25%?
Решение:
Находим номинальную ставку для полугодового начисления процентов:
j = m[(1 + i) 1 / m — 1] = 2[(1 + 0,25) 1/2 — 1] = 0,23607.
Находим номинальную ставку для ежемесячного начисления процентов:
j = m[(1 + i) 1 / m — 1] = 4[(1 + 0,25) 1/12 — 1] = 0,22523.
Таким образом, номинальные ставки 23,61% с полугодовым начислением процентов и 22,52% с ежемесячным начислением процентов являются эквивалентными.
При выводе равенств, связывающих эквивалентные ставки, приравниваются друг к другу множители наращения, что дает возможность использовать формулы эквивалентности простых и сложных ставок:
простая процентная ставка:
сложная процентная ставка:
Пример 2. Предполагается поместить капитал на 4 года либо под сложную процентную ставку 20% годовых с полугодовым начислением процентов, либо под простую процентную ставку 26% годовых. Найти оптимальный вариант.
Решение:
Находим для сложной процентной ставки эквивалентную простую ставку:
i = [(1 + j / m) m • n — 1] / n = [(1 + 0,2 / 2) 2 • 4 — 1] / 4 = 0,2859.
Таким образом, эквивалентная сложной ставке по первому варианту простая процентная ставка составляет 28,59% годовых, что выше предлагаемой простой ставки в 26% годовых по второму варианту, следовательно, выгоднее разместить капитал по первому варианту, т.е. под 20% годовых с полугодовым начислением процентов.
Находим эквивалентную сложную ставку процентов для простой ставки:
Таким образом, процентная ставка 18,64% годовых с полугодовым начислением процентов ниже 20% годовых с полугодовым начислением процентов, то первый вариант выгоднее.
В практической деятельности часто возникает необходимость изменения условий ранее заключенного контракта – объединение нескольких платежей или замене единовременного платежа рядом последовательных платежей. Естественно, что в таких условиях ни один из участников финансовой операции не должен терпеть убыток, вызванный изменением финансовых условий. Решение подобных задач сводится к построению уравнения эквивалентности, в котором сумма заменяемых платежей, приведенная к какому-то одному моменту времени, приравнена к сумме платежей по новому обязательству, приведенному к тому же моменту времени.
Для краткосрочных контрактов консолидация осуществляется на основе простых ставок. В случае с объединением (консолидированием) нескольких платежей в один сумма заменяемых платежей, приведенных к одной и той же дате, приравнивается к новому обязательству:
Пример 3. Решено консолидировать два платежа со сроками 20.04 и 10.05 и суммами платежа 20 тыс. руб. и 30 тыс. руб. Срок консолидации платежей 31.05. Определить сумму консолидированного платежа при условии, что ставка равна 10% годовых.
Решение:
Определим временной интервал между сроками для первого платежа и консолидированного платежа:
t1= 11(апрель) + 31(май) — 1 = 41 день;
для второго платежа и консолидированного платежа:
Отсюда сумма консолидированного платежа будет равна:
= 20’000 • (1 + 41/360 • 0,1) + 30’000 • (1 + 21/360 • 0,1) = 50’402,78 руб.
Таким образом, консолидированный платеж со сроком 31.05 составит 50’402,78 руб.
Конечно, существуют различные возможности изменения условий финансового соглашения, и в соответствии с этим многообразие уравнений эквивалентности. Готовыми формулами невозможно охватить все случаи, возникающие в практической деятельности, но в каждой конкретной ситуации при замене платежей уравнение эквивалентности составляется похожим образом.
Если платеж FV1 со сроком n1 надо заменить платежом FVоб. со сроком nоб. (nоб. > n1) при использовании сложной процентной ставки i, то уравнение эквивалентности имеет вид:
Пример 4. Предлагается платеж в 45 тыс. руб. со сроком уплаты через 3 года заменить платежом со сроком уплаты через 5 лет. Найти новую сумму платежа, исходя из процентной ставки 12 % годовых.
Решение:
Поскольку nоб. > n1, то платеж составит:
Таким образом, в новых условиях финансовой операции будет предусмотрен платеж 56’448 руб.
Источник
Эквивалентность процентных ставок
При заключении финансовых контрактов каждый участник сделки стремится заключить контракт на наиболее выгодных для себя условиях. Условия контракта могут быть различными, и надо иметь возможность сравнивать контракты. При этом различные контракты могут предусматривать различные виды начисления процентов и для сравнения таких контрактов надо разработать способы приведении различных процентных ставок к одному виду. Напомним формулы для вычисления наращенной суммы S для всех видов процентных ставок:
– начисление простых процентов;
– начисление сложных процентов;
– начисление процентов m раз в год;
– простой дисконт (процентный доход, вычитаемый из ссуды в момент ее выдачи);
– учет по сложной учетной ставке;
– учет по сложной учетной ставке m раз в году.
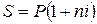
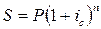
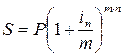
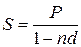
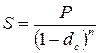
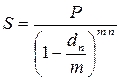
Во всех формулах есть число лет (n), оно может быть дробным.
Две процентные ставки называются эквивалентными, если применение их к одинаковым суммам в течение одинаковых промежутков времени дает одинаковые наращенные суммы.
Приравнивая правые части каких-либо двух из приведенных выше формул и выражая из этого равенства одну процентную ставку через другую, получаем условие эквивалентности соответствующих процентных ставок за n лет.
Пример решения задачи
Определите значение учетной ставки банка, эквивалентной ставке процентов, равной 40 % годовых.
Решение. Рассмотрим будущую стоимость этих сумм для одного года: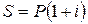 
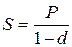
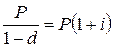
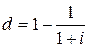
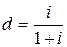
и 
. Так как левые части равны, то равны и правые: 
. Выражая из этого равенства учетную ставку d, получаем: 
или 
.
Таким образом, для заданной i = 40 %
.
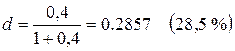
Для расчета эффективности финансовых операций используют сравнительную доходность, которая на основе допущения о равенстве финансовых результатов различных вариантов инвестиций приводит к понятию эквивалентных ставок простых или сложных процентов. Это позволяет получить инструмент корректного сравнения финансовых операций.
Эффективная ставка процентов измеряет относительный доход, который получают в целом за год от начисления процентов несколько раз в год:
(1.6)
Иначе говоря, эффективная ставка показывает, какая годовая ставка сложных процентов дает такой же финансовый результат, что и m-разовое начисление в год по ставке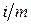 
.
Под эффективной учетной ставкой понимают сложную годовую учетную ставку, эквивалентную номинальной при заданном значении m и вычисляют по формуле:
Пример решения задачи.Банк начисляет проценты на вклад исходя из номинальной ставки 12 % годовых. Определить эффективную (годовую) ставку при ежедневной капитализации процентов.
Решение: m = 365. По формуле (1.6) получим:
, то есть 12,747 %.
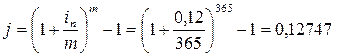
Практические задания:
1. Срок платежа по векселю составляет 6 месяцев. Эффективность операции учета в банке должна составить 120 % годовых. Определить эквивалентное значение учетной ставки.
2. Банк хочет обеспечить себе доходность 90 % годовых. Какую он должен определить учетную ставку, если до погашения векселя осталось 8 месяцев?
Источник