Накопленная доходность как рассчитать

Как считать доходность

Считаем доходность финансовых инструментов и других вложений правильно

Основы

Доходность вложения за некоторый период — это отношение дохода ( I ) от вложения к его размеру ( C ) r = I / C .

По-другому её можно выразить как отношение прироста капитала к его размеру на начало периода r = C 0 ​ C 1 ​ − C 0 ​ ​ .

Отсюда получаем, что размер капитала на начало следующего периода будет равен C 1 ​ = ( 1 + r ) C 0 ​ = R C 0 ​ , а на начало следующего C 2 ​ = R C 1 ​ = R 2 C 0 ​ , и так далее C n ​ = R n C 0 ​ . Но только при условии, что доходность R не зависит от размера капитала (для реальных активов это не всегда так, о чём см. далее). Таким образом, «сложный процент» оказывается заключён уже в самом определении доходности.

То есть, если мы считаем доходность на разовое вложение C 0 ​ , которое через n периодов (обычно в качестве периода берут год) даст капитал в размере C n ​ , это будет R = n C n ​ / C 0 ​

​ = ( C 0 ​ C n ​ ​ ) n 1 ​ , или в процентах годовых r = n C n ​ / C 0 ​

​ − 1 , где n — количество лет (возможно, дробное).

Разумеется, из итогового капитала нужно вычитать все расходы, понесённые в связи с инвестицией.

Доходность с изъятиями и довнесениями

В предыдущем разделе мы посчитали доходность на разовое вложение. А что делать, если размер инвестированного капитала изменяется?

Так как доходность актива мы считаем постоянной, можно просто представить итоговый капитал в момент времени t как сумму независимых вложений D i ​ , сделанных в моменты времени t i ​ . Тогда каждое вложение будет приносить свою доходность t − t i ​ периодов. А изъятие капитала мы просто представляем вложением со знаком минус. C t ​ = R t − t 1 ​ D 1 ​ + R t − t 2 ​ D 2 ​ + …

Итоговый капитал тоже можно представить как изъятие в размере остатка, который ни секунды не приносил доходности: R t − t 1 ​ D 1 ​ + R t − t 2 ​ D 2 ​ + … + R 0 ( − C t ​ ) = 0

Получили уравнение с одним неизвестным — R . Решив его, мы и получим искомую доходность. К сожалению, из-за множества слагаемых в высоких (и часто дробных) степенях, какой-либо формулы для его решения не существует.

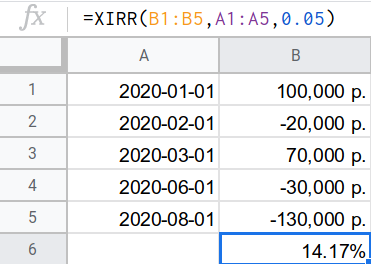
Поэтому его нужно решать численно (или подбором). Функция для решения такого рода уравнений обычно называется XIRR (в русском варианте экселя и родственников — ЧИСТВНДОХ — чистая внутренняя доходность) и принимает на вход даты, размеры вложений (включая изъятие остатка на последнюю дату), и начальное приближение доходности (численный метод не всегда может получить решение, если оно будет далеко от истинного значения, или просто «неудобным»; иногда нужно попробовать разные значения, чтобы получить результат). Выглядит это примерно так:

Как довложения при этом нужно учитывать только расходы, связанные с активом, которые вы несёте из своего кармана. А как изъятия, соответственно, только те суммы, которые вы получаете от него в свой карман.

То есть, если вы как вложения и изъятия учитываете только суммы перевода на брокерский счёт и обратно, то никакие движения денег внутри него учитывать уже не нужно. Если вы получаете дивиденды и купоны на отдельный счёт и используете их — надо учесть как изъятие. А если вам, например, пришлось доплатить налогов с другого счёта — не забудьте оформить их довложением, потому что это расход, связанный с инвестицией, хотя на него и не было ничего куплено.

Аналогично, если вы рассчитываете доходность сдаваемой в аренду квартиры. Все ваши налоги и прочие связанные с ней расходы надо считать как довложения в актив. А из конечной суммы изъятия не забывать вычесть налоги к уплате (или, более корректно, оформить их последним довложением с правильной датой после изъятия продажной стоимости).

Помимо этого, я бы оценивал примерную стоимость и считал за довложения в том числе и трудозатраты на управление активом.

Есть и приближённые способы вычисления доходности актива при наличии изъятий и довложений (например, по средневзвешенному задействованному капиталу), но, в эпоху электронных таблиц и библиотек финансовой математики, они более трудоёмкие, чем точный расчёт по XIRR, поэтому я не стану их описывать.

Взвешенная по времени доходность

Часто вам может быть интересно сравнить результаты своего портфеля с фондовым индексом, или каким-либо другим бенчмарком. Однако на ранних стадиях формирования портфеля, когда суммы довложений и изъятий составляют значительную его часть, время совершения операций может существенно влиять на результаты. Поэтому результат расчёта из предыдущего раздела, «взвешивающий» доходность по размеру задействованного капитала (поэтому называемый MWR, money-weighted return), для сравнения портфеля с индексом непригоден. Нужно сперва полученную доходность очистить от эффекта выбора времени операций (если, конечно, маркет-тайминг не является основой вашей стратегии). Полученная таким образом доходность называется взвешенной по времени (TWR, time-weighted return).

Чтобы её вычислить нужно разбить весь период инвестирования на отрезки, в которые внешних движений не происходило, перемножить доходности на каждом из отрезков, и возвести в степень, обратную продолжительности периода инвестирования (чтобы привести, например, к среднегодовой).

R = ( C 0 ​ C 1 ​ ​ × C 1 ′ ​ C 2 ​ ​ × C 2 ′ ​ C 3 ​ ​ × ⋯ × C n − 1 ′ ​ C n ​ ​ ) t 1 ​ , здесь C n ′ ​ — это капитал на конец n -го отрезка после учёта довложения/изъятия. Но не забывайте уменьшать C n ​ на размер понесённых расходов, если они ещё не отражены в этом значении.

Характерная доходность

Все предыдущие методы для расчёта доходности учитывают только величины капитала на начало и конец периода инвестирования. Если у нас достаточно волатильный инструмент/портфель, то рассчитанная доходность может очень сильно зависеть не только от удачи в выборе моментов довложений/изъятий (которую устраняет расчёт доходности, взвешенной по времени), но и от выбора начальной и конечной точки. Чтобы устранить и этот шум, нужно рассчитывать доходность характерную.

Характерная доходность — это скорость роста капитала, очищенная от волатильности, медианная доходность по всем возможным интервалам внутри рассматриваемого периода. Чтобы её определить нам надо построить линию тренда на графике роста логарифма размера капитала (потому что нам важен относительный рост, а абсолютный).

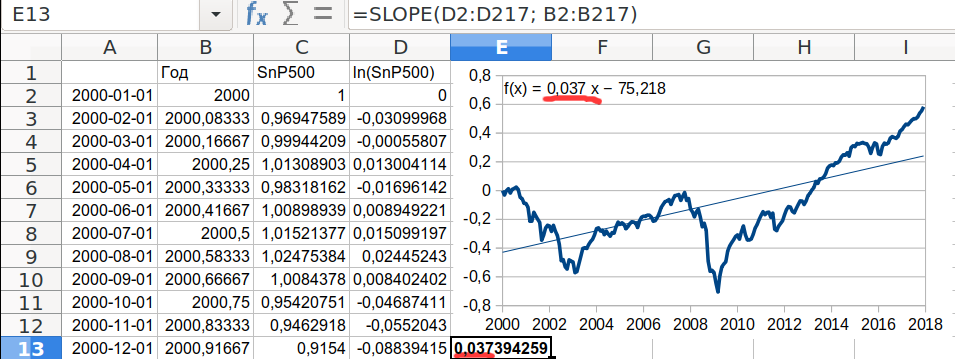
Это можно сделать в электронной таблице (функция «вставить линию тренда» и показать формулу зависимости на графике есть практически везде), или выполнить приближение соответствующей линейной модели другим удобным вам способом (в том же экселе нужный результат даст функция SLOPE/НАКЛОН). Работая в экселе не забывайте, что по оси x графика должен быть отложен именно год числом, а не дата. Иначе вы получите не годовую доходность, а дневную (хотя пересчитать её в годовую тривиально).

В примере ниже показано, что характерная реальная доходность индекса SnP500 с 2000 по 2018 составила 3,7%г.

Номинальная и реальная доходность

Используя в расчётах те суммы довложений/изъятий, которые вы фактически сделали и те размеры капитала, которые фактически зафиксировали, вы будете получать номинальные доходности. Однако, в ситуациях с высокой/неравномерной инфляцией (США сюда тоже относятся) эти доходности совершенно неинформативны.

Чтобы получить реальную доходность, необходимо все суммы, участвующие в расчётах, скорректировать на инфляцию, разделив на значение соответствующего индекса на дату вложения/изъятия/фиксации. Дата начала и направление отсчёта индекса и его величина значения при этом не имеют.

В качестве индекса традиционно используется индекс потребительских цен, но можно использовать и другие: однодневных межбанковских кредитов, доходности гособлигаций, дефлятор ВВП, цен производителей и т.д. в зависимости от целей расчёта доходности. Т.е. реальная доходность не однозначна и требует указания на индекс, с помощью которого она рассчитывалась. По умолчанию предполагается, что использован индекс потребительских цен страны происхождения инструмента, что не всегда удобно (например, хотя характерная реальная доходность индекса SnP500 по ИПЦ США в предыдущем примере была 3,7%г, по ИПЦ РФ она будет отрицательной, примерно −1%г).

Реальные активы

У реальных активов, в отличие от идеальных, доходность зависит от объёма вложенного капитала, причём иногда довольно сложным образом. Рассмотрим основные составляющие этой зависимости.

1. Нижний барьер капитализации. «Довложение» суммы меньшей этого барьера не приведёт к росту дохода (т.е. доходность на вложенный капитал упадёт). Барьер возникает из-за того, что существует неделимая единица актива, и суммы меньшие стоимости этой единицы будут простаивать.
2. Верхний барьер капитализации. Рост задействованного капитала сверх барьера не ведёт к росту дохода, доходность на капитал падает. Эффект связан с тем, что любая доходность, в конечно итоге, происходит от создания и продажи экономических благ. Если ресурсы/мощности/рынок сбыта задействованы полностью, то вливание нового капитала роста дохода уже не принесёт.
3. Убывающая отдача. Возникает с приближением к верхнему барьеру капитализации (или какому-то из промежуточных): получение каждой следующей единицы дохода начинает стоить всё бо́льших вложений. Также может быть следствием конкуренции множества агентов за фиксированный доход, который распределяется пропорционально вложенным средствам. Так работают финансовые рынки: размер прибыли которую могут распределить компании, и размер процентов, которые они готовы заплатить по долгам, на коротких горизонтах фиксированы, поэтому при резком росте вложенного в них капитала, доходность каждой последующей единицы падает.
4. Экономия на масштабе. В основном характерна для производственных активов, где велика доля фиксированных издержек, и при росте выпуска каждая последующая единица несёт себе меньшую их долю т.е. обходится дешевле. Однако может возникать и как следствие преодоления нижнего барьера капитализации: если стоимость единицы актива, скажем, 200Кр, то каждые последующие 200Кр капитала приводят к тому, что сокращается время простоя полученного дохода до следующей покупки актива, а, следовательно, растёт эффективная доходность.

Манипуляции доходностью

В интернете находится огромное количество способов извлечения огромной доходности из достаточно простой инвестиционной деятельности. Я здесь имею в виду не мошенников, которые предлагают отдать им деньги в обмен на обещания этой высокой доходности, а именно самостоятельную работу. Как правило, практически все они показывают привлекательные цифры за счёт ошибок в расчёте доходности (и игнорирования операционных рисков, но это тема для другой статьи).

1. В расходы на инвестицию учитываются только стоимость самого объекта инвестирования, но не сопутствующие затраты, которые могут быть сопоставимы или даже больше. Особенно любят забывать стоимость проведения сделок, текущие платежи (например, коммунальные) и налоги. Никто в принципе не учитывает стоимость трудозатрат.
2. Игнорируются барьеры капитализации и убывающая отдача. Вы можете, условно, сдавать гараж стоимостью 200Кр за 2Кр/мес, имея по итогам года после всех расходов 20Кр или 10%, но пока вы 10 лет копите на следующий, эти деньги должны где-то лежать под меньшую доходность. А после десятого гаража вы уже хотите нанять управляющего, только никто не соглашается работать за 16Кр/мес, которые этот десяток гаражей приносит.
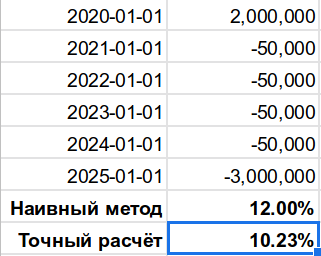
3. Используется «наивный» расчёт [суммарный доход]/[суммарный расход]/[количество лет], без учёта сложных процентов и временно́й стоимости денег. Как показано на рисунке ниже, даже для небольшого промежутка времени разница такого метода с точным может быть достаточно велика, чтобы склонить к ошибочному решению.

Не ведитесь на манипуляции, считайте доходность правильно.

Здесь я выкладываю лишь собственные размышления/исследования/расчёты, иногда собственное же изложение чужих мнений или результатов исследований. Размещённая информация может содержать ошибки, быть неактуальной на момент прочтения, допускать множество интерпретаций и проч. Я не занимаюсь образовательной деятельностью и не даю инвестиционных рекомендаций ни на этом сайте, ни в частном порядке.

Может быть, вам показалось, но способов получить гарантированную доходность за счёт каких бы то ни было финансовых инструментов, портфелей или торговых стратегий НЕ СУЩЕСТВУЕТ. Хуже того, способов гарантированно сохранить свой капитал тоже НЕ СУЩЕСТВУЕТ.

Материалы сайта могут быть использованы на условиях лицензии CC BY-NC-SA.
© Андрей Болкисев, 2021.

Источник

Правильный расчет среднегодовой доходности в инвестициях

Любой инвестор рано или поздно должен подвести итоги и рассчитать доходность инвестиций. Так как цифры вроде 125% за 5 лет мало информативны, то доходность принято приводить доходность к годовым значениям. Такую доходность называют среднегодовой доходностью. В случае с 125% за 5 лет среднегодовая доходность равна 17,6%. 125% принято назвать накопленной доходностью.

Как рассчитать среднегодовую доходность

Если период инвестиций измеряется в годах, то формула среднегодовой доходности выглядит следующим образом:

R – накопленная доходность
r – среднегодовая доходность
T– срок инвестиций (в годах)

Эта формула предполагает капитализацию процентов. Её нельзя применять, например, в тех случаях, когда дивиденды выводились из инвестиций (не реинвестировались).

В случае произвольного промежутка инвестиций среднегодовая доходность считается по аналогии.

R – накопленная доходность
r – среднегодовая доходность
T– срок инвестиций (в месяцах)

Здесь период инвестиций измеряется в месяцах. Если необходимо рассчитать с точностью до дней, то 12 надо заменить на 365.

Пример вычисления:

Инвестор получил доходность 12% за 16 месяцев. Чему равна его годовая доходность?

Основные ошибки при вычислениях

Чаще всего начинающие инвесторы допускают ошибку, считая следующим образом (пример с доходностью 125% за 5 лет):

Или в примере с 12% за 16 месяцев:

Такой вариант расчетов в инвестициях использовать нельзя, так как при этом не учитывается капитализация процентов.

Источник

Расчет годовой доходности и стандартного отклонения

Автор: Дмитрий Никитенко
Дата записи

Чтобы вы всегда могли проверить данные, найденные в интернете, или рассчитать доходность собственных инвестиций, в этой статье я научу вас делать это правильно.

Приведенные здесь методы расчета подходят для любых электронных таблиц – Excel, Google Sheets или LibreOffice. А то, что не использует экселевские функции, можно просто считать в любом калькуляторе, например, встроенном в Google или Яндекс.

Расчет доходности инвестиций

Доходность в процентах за любой период можно рассчитать двумя способами:

1. знакомая многим формула: (конец периода — начало периода) / начало периода = (110 — 100) / 100 = 10%;
2. и более короткая версия: конец периода / начало периода — 1 = 110 / 100 — 1 = 10%. Мы будем считать доходность за год по второй формуле, потому что она немного короче и её результат в разах (до вычитания единицы) нам ещё пригодится.

Дальше для простоты мы будем называть её общей доходностью.

Расчет средней годовой доходности (и приведение доходности к годовой)

Под средней годовой доходностью обычно понимается среднегодовая ставка доходности, которая приводит начальную сумму вложений к конечной путем последовательного начисления этой ставки на результат предыдущего года.

Это не просто средняя арифметическая доходностей отдельных лет, а среднее геометрическое. Проще говоря, какую прибыль в процентах вы должны каждый год получать, чтобы из суммы А в итоге получилась сумма Б.

Средняя геометрическая доходность учитывает эффект сложного процента (капитализации процентов и возникающего в следствие этого экспоненциального роста), поэтому всегда будет меньше арифметической средней.

Другое название средней геометрической доходности из англоязычных источников, которое вам может встречаться — “compound annual growth rate” (CAGR).

Рассмотрим расчет годовой доходности для нескольких видов входящих данных, которые обычно имеют инвесторы. Под среднегодовой доходностью далее будем понимать именно среднюю геометрическую или CAGR.

Есть общая доходность за период

Если известно какую доходность принес актив за весь период, годовую доходность можно найти по формуле:

где x – доходность за весь период в процентах, n – количество полных лет в периоде, ^ – возведение в степень.

Например, если за 3 года доходность составила 30%, то среднегодовая доходность будет равно не 30% / 3 = 10%, а (0.3 + 1) ^ (1 / 3) — 1 = 9,14%.

Проверим: начальная сумма 100, конечная – 130:

• 100 + 100 * 9,14% = 109,14
• 109,14 + 109,14 * 9,14% = 119,12
• 119,12 + 119,12 * 9,14% = 130

Прибавление единицы нужно, чтобы перевести известную доходность из процентов в разы, а вычитание в конце – для перевода обратно из разов в проценты (напомню, что 30% = 0.3, в Excel можно записать оба варианта, разницы нет).

В Excel (или других электронных таблицах) возвести в степень можно либо с помощью того же знака ^, либо функцией СТЕПЕНЬ((x + 1); (1 / n)) — 1.

Есть начальная и конечная сумма

Если у вас есть результат инвестиций за известный период в виде сумм на начало и конец этого периода, то всё, что нужно сделать – это узнать общую доходность (формула та же, из начала статьи – 130 / 100 — 1 = 30%) и с ней рассчитать среднегодовую по формуле из предыдущего пункта.

Есть доходности по годам

Если у вас есть ряд доходностей за отдельные годы или вы можете найти их по ценам, то расчет среднегодовой доходности сводится к двум способам:

1. поиску среднего геометрического этих доходностей, выраженных в разах;
2. умножению этих разов для получения общей доходности и расчету как в предыдущих пунктах.

Первый вариант считать вручную нет смысла, поэтому лучше сразу обратиться к Excel и воспользоваться функцией СРГЕОМ (GEOMEAN). В неё надо передать либо список значений, либо диапазон ячеек, в которых у вас записаны годовые доходности, выраженные в разах.

Для примера посчитаем так инфляцию в России за последние 5 лет:

• 2014: 11,35% + 1 = 1,1135
• 2015: 12,91% + 1 = 1,1291
• 2016: 5,39% + 1 = 1,0539
• 2017: 2,51% + 1 = 1,0251
• 2018: 4,26% + 1 = 1,0426

СРГЕОМ(1,1135; 1,1291; 1,0539; 1,0251; 1,0426) — 1 = 7,2%

СРГЕОМ(A1:A5) — 1 = 7,2% (представим, что в ячейках те же доходности в разах)

Второй вариант расчета через умножение будет выглядеть так:

(1,1135 * 1,1291 * 1,0539 * 1,0251 * 1,0426) ^ (1 / 5) — 1 = 7,2%

Есть доходность за неполный год

Пока мы рассмотрели только полные годовые периоды, но среднегодовую доходность можно считать и для неполных лет. Например, какой-то актив за 4 года и 6 месяцев принес вам 50%. Чтобы аннуализировать эту доходность (привести к среднегодовой, в степень нужно подставить 4,5:

(0.5 + 1) ^ (1 / 4,5) — 1 = 9,43%

Привести месяцы неполного года к дробной части можно просто разделив их на 12:

• 6 / 12 = 0,5;
• 8 / 12 = 0,67 и так далее.

По аналогичному принципу можно взять доходность за прошедшее количество дней в году и привести её к годовой:

(x + 1) ^ (252 / n) — 1, где x – доходность за эти дни в процентах, n – количество дней, а 252 — количество торговых дней в году.

Если доходность за 100 дней года составила 3%, то среднегодовая будет равна:

(0,03 + 1) ^ (252 / 100) — 1 = 7,7%.

Вместо торговых дней можно брать и календарные, то есть 365 — выбор зависит от ваших данных и целей расчета.

Приведение дневной или месячной доходности к годовой

Если вы располагаете среднедневной или среднемесячной доходностью (геометрической), эти данные можно аннуализировать по таким формулам:

• для дневной доходности: (x + 1) ^ 252 — 1, где x – доходность в процентах и 252 — число торговых дней в году;
• для месячной доходности: (x + 1) ^ 12 — 1.

Например, приведение дневной доходности 0,03% может выглядеть так: (0,0003 + 1) ^ 252 — 1 = 7,9%. Естественно, то же самое можно делать для недельной или квартальной доходности (возводя в 52 или 4 степень).

При этом аннуализированное СКО рассчитывается по другой формуле: x * SQRT(252), то есть среднедневную волатильность нужно умножить на квадратный корень из количества торговых дней (либо месяцев и т. д.).

Расчет годовой доходности с учетом пополнений и изъятий (движения средств)

Все вышеперечисленные способы подходят для расчета доходности активов или экономических показателей в вакууме, но личные инвестиции сопряжены с периодическими пополнениями портфеля или изъятиями средств из него.

Если просто рассчитать доходность способами выше, она окажется искаженной этими движениями денег. Например, если на начало года у вас было 100 000 руб., потом вы купили активы на 80 000 руб., а в конце года стоимость портфеля составила 200 000 руб., это не значит, что вы заработали 200000 / 100000 — 1 = 100%.

В таких случаях есть несколько способов посчитать свой финансовый результат, устранив движения средств из показателя доходности. Наиболее удобный из них – это расчет внутренней нормы (или ставки) доходности (internal rate of return, IRR), потому что для этого есть две функции в Excel.

1. ВСД (IRR) – для регулярных во времени пополнений или изъятий (например, каждый месяц, квартал или год);
2. ЧИСТВНДОХ (XIRR) – для нерегулярных, что и применяется в реальной жизни.

Всё, что нужно сделать, это передать в функцию ЧИСТВНДОХ диапазоны ячеек с суммами и датами, при этом пополнения будут положительными числами, а изъятия отрицательными (или наоборот), а последней должна быть текущая стоимость портфеля, как если бы вы сняли всё в последний день. Если те 80 000 руб. мы положили 6 июля, то для нашего примера это будет выглядеть так:

• 2019-01-01: -100000
• 2019-07-06: -80000
• 2019-12-31: 200000

Годовая доходность: ЧИСТВНДОХ(B1:B3; A1:A3) = 14,56%.

В колонке A были даты, в B – суммы.

Расчет стандартного отклонения

В любых электронных таблицах рассчитать стандартное отклонение не составляет труда. Его можно считать для годовых или любых других доходностей, выраженных в процентах или разах, приводить месячное стандартное отклонение к годовому и так далее. Стандартное отклонение также называется среднеквадратическим или СКО.

Для этого нам понадобится функция СТАНДОТКЛОН (STDEV), куда достаточно просто передать диапазон ячеек с доходностями. Она рассчитывает СКО для выборки из генеральной совокупности, что нам и нужно.

Если взять пример с инфляцией в России за последние 5 лет, получим такой результат:

СТАНДОТКЛОН(11,35%; 12,91%; 5,39%; 5,39%; 4,26%) = 3.96%.

Источник