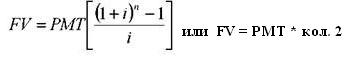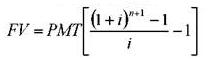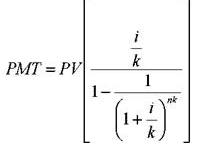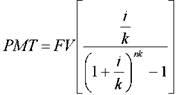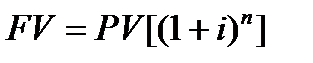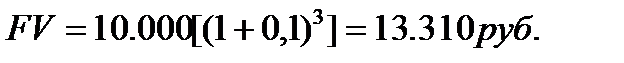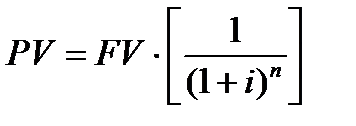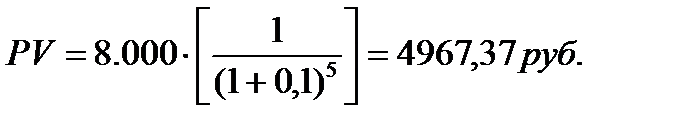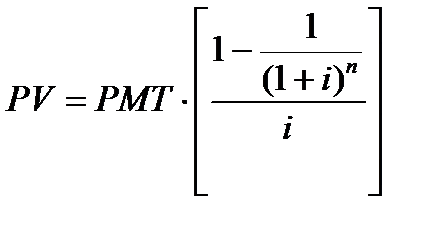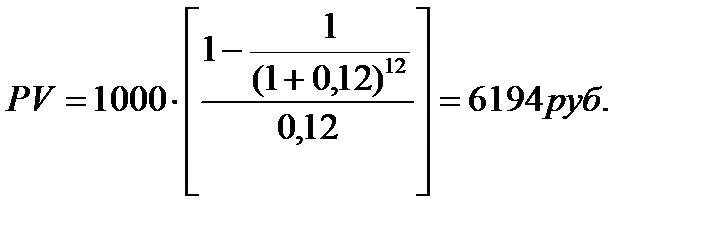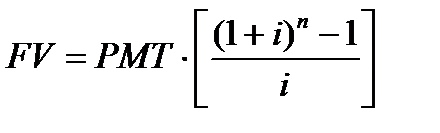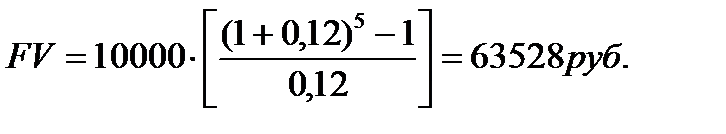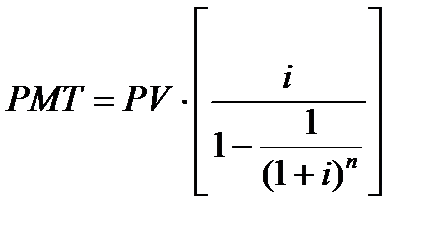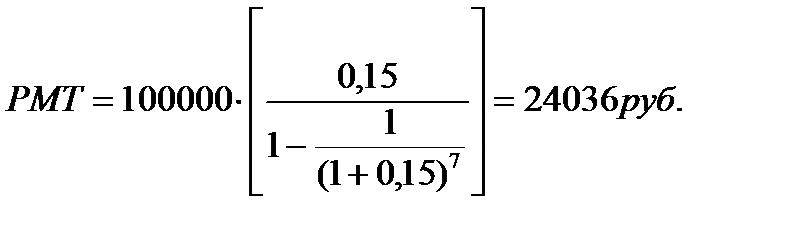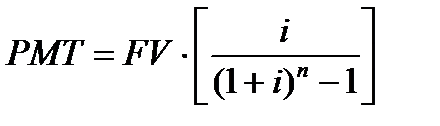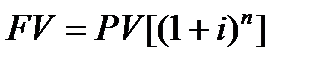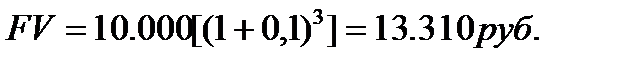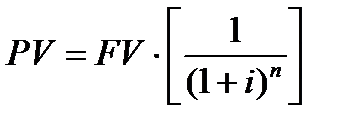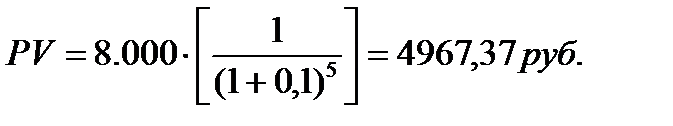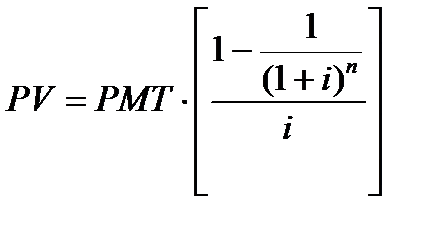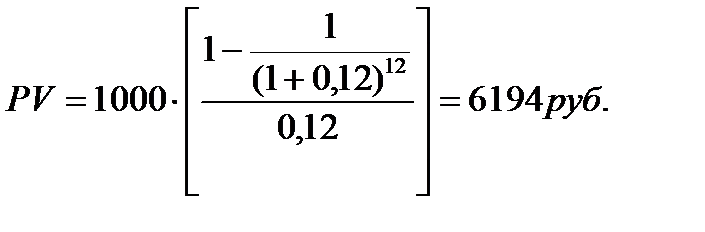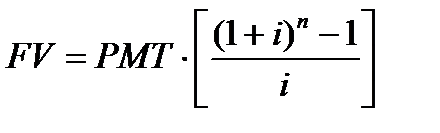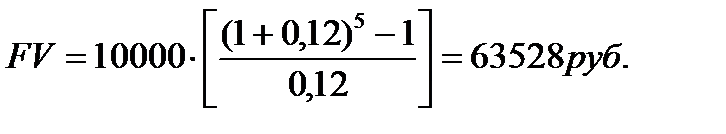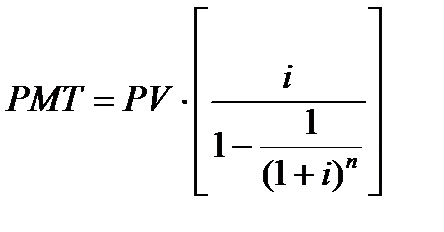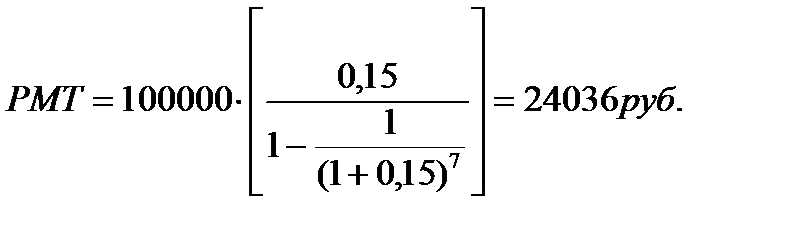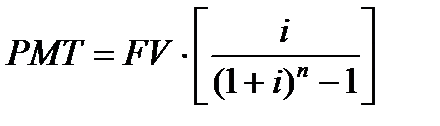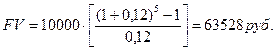—>РЕПЕТИТОР ОЦЕНЩИКА
Специализированный сайт для студентов-оценщиков
Формулы сложных процентов

Будущая стоимость денежной единицы ( FV) – накопленная сумма денежной единицы. Накопленная сумма денежной единицы показывает, какую сумму будет составлять денежная единица, вложенная сегодня, через определенный период времени при определенной ставке дисконта (доходности).
Начисление процентов 1 раз в год: FV = PV * [(1+ i ) n ] или FV = PV * кол.1
Начисление процентов чаще, чем один раз в год: FV = PV * [(1+ i / k ) nk ]

Текущая стоимость денежной единицы ( P V) или текущая стоимость реверсии (перепродажи) показывает, какую сумму нужно иметь сегодня, чтобы через определенный период времени при определенной ставке дисконта (доходности) получить сумму, равную денежной единице, то есть какой сумме сегодня эквивалентна денежная единица, которую мы рассчитываем получить в будущем через определенный период времени.
Начисление процентов 1 раз в год: PV = FV * [1/(1+ i ) n ] или PV = FV * кол.4
Начисление процентов чаще, чем один раз в год: PV = FV * [1/(1+ i / k ) nk ]

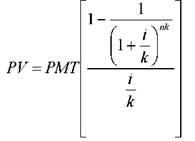
Текущая стоимость аннуитета показывает, какой сумме денежных средств сегодня эквивалентна серия равномерных платежей в будущем, равных одной денежной единице, за определенное количество периодов при определенной ставке дисконта.
Начисление процентов 1 раз в год: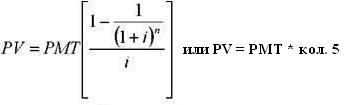
Начисление процентов чаще, чем один раз в год:
Накопление денежной единицы за период FV — будущая стоимость серии равновеликих периодических платежей (поступлений). Фактор накопления единицы за период показывает, какой будет стоимость серии равных сумм, депонированных в конце каждого периодического интервала по истечении установленного срока.
Обычный аннуитет:
Авансовый аннуитет:

Взнос на амортизацию денежной единицы — это величина регулярного периодического платежа в счет погашения кредита, выданного на определенный период при процентной заданной ставке. Это величина, обратная текущей стоимости аннуитета. Амортизация в данном случае – это погашение (возмещение, ликвидация) долга в течение определенного времени.
Начисление процентов чаще, чем один раз в год:

Фактор фонда возмещения — показывает аннуитетный платеж, который необходимо депонировать под заданный процент в конце каждого периода для того, чтобы через заданное число периодов получить искомую сумму.
Начисление процентов чаще, чем один раз в год:
Источник
Шесть функций денежной единицы.
Для определения стоимости инвестиционного проекта или собственности необходимо определить текущую стоимость денег, которые будут получены через некоторое время в будущем. В условиях инфляции деньги изменяют свою стоимость с течением времени. Основными операциями, позволяющими сопоставить разновременные деньги являются операции накопления (наращивания) и дисконтирования.
Накопление – это процесс приведения текущей стоимости денег к их будущей стоимости при условии, что вложенная сумма будет находиться на счету в течение определенного времени, принося периодически накапливаемый процент.
Дисконтирование – процесс приведения денежных поступлений от инвестиций к их текущей стоимости.
1 функция. Определим будущую стоимость денежной единицы (накопленная сумма денежных единиц)
FV — будущая стоимость денежной единицы,
PV – текущая стоимость денежной единицы,
i – ставка дохода,
n – число периодов накопления в годах.
Задача. Определить какая сумма будет накоплена на счете к концу 3 года, если сегодня положить на счет под 10 % годовых 10 тыс. руб.
2 функция. Текущая стоимость денежной единицы (текущая стоимость реверсии перепродажи)
Задача. Сколько нужно вложить сегодня в инвестиционный проект, чтобы к концу 5 года получить 8 тыс.руб. Ставка дохода 10%.
3 функция. Определение текущей стоимости аннуитета.
Аннуитет – это серия равновеликих платежей (поступлений), отстоящих друг от друга на один и тот же промежуток времени.
Выделяют обычный и авансовый аннуитет. Если платежи осуществляют в конце каждого периода, то аннуитет обычный; если вначале – авансовый.
Формула текущей стоимости обычного аннуитета:
PMT – равновеликие периодические платежи.
Задача. Договор аренды дачи составлен на 1 год. Платежи осуществляются ежемесячно по 1 тыс.руб. Определить текущую стоимость арендных платежей при 12% ставке дисконтирования. n = 12 (число периодов – месяцев).
4 функция. Накопление денежной единицы за период. В результате использования данной функции определяется будущая стоимость серии равновеликих периодических платежей или поступлений.
Задача. Определить сумму, которая будет накоплена на счете, приносящем 12% годовых, к концу 5 года, если ежегодно откладывать на счет 10 тыс.руб.
5 функция. Взнос на амортизацию денежной единицы.
Данная функция является обратной величиной текущей стоимости обычного аннуитета.
Амортизация – это процесс, определяемый данной функцией, и включает проценты по кредиту и оплату основной суммы долга.
Задача. Определить, какими должны быть ежегодные платежи, чтобы к концу 7 года погасить кредит 100 000 руб., выданный под 15% годовых.
Аннуитет может быть как поступлением (входящим денежным потоком), так и платежом (исходящим денежным потоком), по отношению к инвестору. Поэтому данная функция может быть использована в случае расчета величины равновеликого взноса на погашение кредита при известном числе взносов и заданной процентной ставке. Такой кредит называется самоамортизирующийся кредит.
6 функция. Рассматривает фактор фонда размещения и является обратной функции накопления единицы за период.
Для определения величины платежа используется следующая формула:
Задача. Определить, какими должны быть платежи, чтобы к концу 5 года иметь на счете при ставке 12% годовых 100 000 руб.
Источник
Шесть функций денежной единицы.



Для определения стоимости инвестиционного проекта или собственности необходимо определить текущую стоимость денег, которые будут получены через некоторое время в будущем. В условиях инфляции деньги изменяют свою стоимость с течением времени. Основными операциями, позволяющими сопоставить разновременные деньги являются операции накопления (наращивания) и дисконтирования.
Накопление – это процесс приведения текущей стоимости денег к их будущей стоимости при условии, что вложенная сумма будет находиться на счету в течение определенного времени, принося периодически накапливаемый процент.
Дисконтирование – процесс приведения денежных поступлений от инвестиций к их текущей стоимости.
1 функция. Определим будущую стоимость денежной единицы (накопленная сумма денежных единиц)
FV — будущая стоимость денежной единицы,
PV – текущая стоимость денежной единицы,
i – ставка дохода,
n – число периодов накопления в годах.
Задача. Определить какая сумма будет накоплена на счете к концу 3 года, если сегодня положить на счет под 10 % годовых 10 тыс. руб.
2 функция. Текущая стоимость денежной единицы (текущая стоимость реверсии перепродажи)
Задача. Сколько нужно вложить сегодня в инвестиционный проект, чтобы к концу 5 года получить 8 тыс.руб. Ставка дохода 10%.
3 функция. Определение текущей стоимости аннуитета.
Аннуитет – это серия равновеликих платежей (поступлений), отстоящих друг от друга на один и тот же промежуток времени.
Выделяют обычный и авансовый аннуитет. Если платежи осуществляют в конце каждого периода, то аннуитет обычный; если вначале – авансовый.
Формула текущей стоимости обычного аннуитета:
PMT – равновеликие периодические платежи.
Задача. Договор аренды дачи составлен на 1 год. Платежи осуществляются ежемесячно по 1 тыс.руб. Определить текущую стоимость арендных платежей при 12% ставке дисконтирования. n = 12 (число периодов – месяцев).
4 функция. Накопление денежной единицы за период. В результате использования данной функции определяется будущая стоимость серии равновеликих периодических платежей или поступлений.
Задача. Определить сумму, которая будет накоплена на счете, приносящем 12% годовых, к концу 5 года, если ежегодно откладывать на счет 10 тыс.руб.
5 функция. Взнос на амортизацию денежной единицы.
Данная функция является обратной величиной текущей стоимости обычного аннуитета.
Амортизация – это процесс, определяемый данной функцией, и включает проценты по кредиту и оплату основной суммы долга.
Задача. Определить, какими должны быть ежегодные платежи, чтобы к концу 7 года погасить кредит 100 000 руб., выданный под 15% годовых.
Аннуитет может быть как поступлением (входящим денежным потоком), так и платежом (исходящим денежным потоком), по отношению к инвестору. Поэтому данная функция может быть использована в случае расчета величины равновеликого взноса на погашение кредита при известном числе взносов и заданной процентной ставке. Такой кредит называется самоамортизирующийся кредит.
6 функция. Рассматривает фактор фонда размещения и является обратной функции накопления единицы за период.
Для определения величины платежа используется следующая формула:
Задача. Определить, какими должны быть платежи, чтобы к концу 5 года иметь на счете при ставке 12% годовых 100 000 руб.
Источник
Шесть функций денежной единицы
Для определения стоимости инвестиционного проекта или собственности необходимо определить текущую стоимость денег, которые будут получены через некоторое время в будущем. В условиях инфляции деньги изменяют свою стоимость с течением времени. Основными операциями, позволяющими сопоставить разновременные деньги являются операции накопления (наращивания) и дисконтирования.
Накопление – это процесс приведения текущей стоимости денег к их будущей стоимости при условии, что вложенная сумма будет находиться на счету в течение определенного времени, принося периодически накапливаемый процент.
Дисконтирование – процесс приведения денежных поступлений от инвестиций к их текущей стоимости.
1 функция. Определим будущую стоимость денежной единицы (накопленная сумма денежных единиц)
FV — будущая стоимость денежной единицы,
PV – текущая стоимость денежной единицы,
i – ставка дохода,
n – число периодов накопления в годах.
Задача. Определить какая сумма будет накоплена на счете к концу 3 года, если сегодня положить на счет под 10 % годовых 10 тыс. руб.
2 функция. Текущая стоимость денежной единицы (текущая стоимость реверсии перепродажи)
Задача. Сколько нужно вложить сегодня в инвестиционный проект, чтобы к концу 5 года получить 8 тыс.руб. Ставка дохода 10%.
3 функция. Определение текущей стоимости аннуитета.
Аннуитет – это серия равновеликих платежей (поступлений), отстоящих друг от друга на один и тот же промежуток времени.
Выделяют обычный и авансовый аннуитет. Если платежи осуществляют в конце каждого периода, то аннуитет обычный; если вначале – авансовый.
Формула текущей стоимости обычного аннуитета:
PMT – равновеликие периодические платежи.
Задача. Договор аренды дачи составлен на 1 год. Платежи осуществляются ежемесячно по 1 тыс.руб. Определить текущую стоимость арендных платежей при 12% ставке дисконтирования. n = 12 (число периодов – месяцев).
4 функция. Накопление денежной единицы за период. В результате использования данной функции определяется будущая стоимость серии равновеликих периодических платежей или поступлений.
Задача. Определить сумму, которая будет накоплена на счете, приносящем 12% годовых, к концу 5 года, если ежегодно откладывать на счет 10 тыс.руб.
5 функция. Взнос на амортизацию денежной единицы.
Данная функция является обратной величиной текущей стоимости обычного аннуитета.
Амортизация – это процесс, определяемый данной функцией, и включает проценты по кредиту и оплату основной суммы долга.
Задача. Определить, какими должны быть ежегодные платежи, чтобы к концу 7 года погасить кредит 100 000 руб., выданный под 15% годовых.
Аннуитет может быть как поступлением (входящим денежным потоком), так и платежом (исходящим денежным потоком), по отношению к инвестору. Поэтому данная функция может быть использована в случае расчета величины равновеликого взноса на погашение кредита при известном числе взносов и заданной процентной ставке. Такой кредит называется самоамортизирующийся кредит.
6 функция. Рассматривает фактор фонда размещения и является обратной функции накопления единицы за период.
Для определения величины платежа используется следующая формула:
Задача. Определить, какими должны быть платежи, чтобы к концу 5 года иметь на счете при ставке 12% годовых 100 000 руб.

Источник