- Модель CAPM – что это простыми словами, пример расчета
- Что такое модель CAPM
- Для чего необходима модель оценки капитальных активов
- Формула расчета
- Расчет модели CAPM в Excel
- Как устроена модель CAPM
- Как можно использовать модель CAPM
- Где применяется модель CAPM
- Преимущества и недостатки модели CAPM
- Пример расчета
- Заключение
- Модель доходности финансовых активов (САPМ).
Модель CAPM – что это простыми словами, пример расчета
CAPM (Capital Asset Pricing Model) – одна из методик оценки стоимости активов акционерного общества с точки зрения рисков, присущих как непосредственно оцениваемому активу, так и рынку в целом.
Модель CAPM построена на предположении: инвесторы заинтересованы в получении дохода выше, чем доход по безрисковым активам.
CAPM – это метод, который может применяться в теории, на практике его использование возможно лишь в некоторых случаях, в комбинации с другими методиками.
Сегодня мы рассмотрим модель оценки капитальных активов CAPM: формулу расчета этого показателя, его применение на практике, преимущества и недостатки.
Что такое модель CAPM
Как известно, стоимость акционерного общества определяется стоимостью его активов. В данном случае под активами понимают не основные фонды, а финансовые инструменты, эмитентом которых является предприятие.
Предпосылкой CAPM стала гипотеза эффективного рынка капитала, появившаяся в начале XX века. Эта гипотеза основана на том, что рынок является прозрачным, и любые изменения быстро отражаются на стоимости акций. В целом рынок «заточен» на долгосрочные инвестиции.
Современная модель оценки капитальных активов была разработана в середине XX века американским экономистом Гарри Марковицем. Далее метод CAPM был взят на вооружение другими финансовыми гуру: Джоном Линтнером, Джеком Л. Трейнором и Уильямом Шарпом. Последний в 1964 г. разработал модификацию модели, которая используется по сей день. Иногда модель капитальных активов CAPM называют моделью Шарпа.
Итак, на чем основана CAPM model? Попытаемся объяснить простыми словами.
Предположим, есть некий безрисковый актив с минимальной доходностью и практически нулевой волатильностью. Безрисковым средством в модели CAPM обычно выступают государственные облигации. Помимо этого, в портфеле мы имеем акции предприятия нефтедобывающего комплекса. Эти бумаги могут принести неплохой доход, однако уж очень зависят от внешней ситуации, в том числе политической. Какова цель инвестора? Как сбалансировать портфель?
Если наш инвестор очень осторожен, то в его портфеле будут преобладать ОФЗ. Да, он не получит высокий доход, но и ничего не потеряет. А если он все-таки хочет, чтобы его деньги работали и приносили прибыль, то он будет двигаться в сторону увеличения доли бумаг с высокой волатильностью. При этом должно соблюдаться общее правило: если эти бумаги начнут падать и приносить убыток, общая должность портфеля не должна быть ниже, чем ставка доходности по ОФЗ.
Для чего необходима модель оценки капитальных активов
Итак, на чем основана модель оценки капитальных активов? Инвестор должен представлять, какой доход он может получить за то, что рискует своими деньгами.
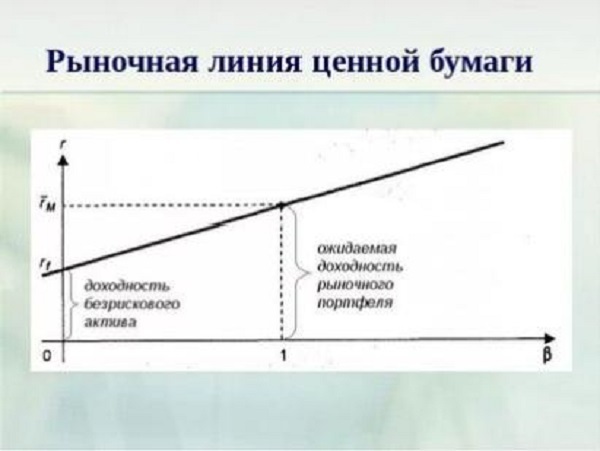
Наглядно CAPM представлена на графике:
Модель CAPM описывает зависимость между доходностью актива, ставкой по безрисковым инструментам и рыночному риску в целом.
CAPM включает элементы:
- доходность безрискового актива;
- ожидаемая общая доходность портфеля;
- общая рыночная доходность;
- чувствительность инструмента к колебаниям рынка (коэффициент β).
Итак, CAPM применяется для оценки доходности ценной бумаги или проекта с учетом систематического (недиверсифицируемого) риска.
Недиверсифицируемый риск – это риск, связанный с отсутствием стабильности в получении дохода. Так, в одном году доходность может быть максимальная, а в следующем периоде оказаться нулевой. Подобные риски присущи ценным бумагам российских компаний, в т.ч. «голубым фишкам».
Возникает резонный вопрос: как рассчитывать или где взять значение коэффициента β? Этот показатель берется из данных статистики. Можно рассчитать коэффициент самостоятельно, используя функции линейной регрессии в Excel, что мы и сделаем в примере ниже. Для этого нужны данные доходности за определенный период по анализируемому активу и в целом по рынку. Для российских бумаг обычно используются индексы РТС или ММВБ, для зарубежных – S&P 500, NASDAQ и др.
Поскольку значения индекса основаны на данных за предыдущие периоды, а само понятие систематического риска говорит о непредсказуемости изменения цены и доходности инструмента, применять расчеты на практике следует с осторожностью. Тем не менее рассчитаем Capital Asset Pricing Model по формуле и в Excel, используя данные по котировкам, находящиеся в свободном доступе.
Формула расчета
Формула CAPM выглядит так:
\[ RE=Rf + β*(Rm – Rf), где: \]
\( RE \) – ожидаемая ставка;
\( Rf \) – ставка по безрисковым инструментам;
\( Rm \) – усредненная прибыль по портфелю в целом;
\( β \) – коэффициент чувствительности актива к колебаниям рынка.
Например, средняя ставка по ОФЗ – 4%. Ожидаемая доходность по портфелю – 20%. Коэффициент β – 0,5.
Приведем таблицу значений β:
| Значение | Комментарий | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| β > 1 | Инструмент чувствителен к колебаниям рынка | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| β = 1 | Доходность актива равна доходности по рынку | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0 Читайте также Реинвестирование: что это простыми словами? Виды, формы и особенности реинвеста \[ RE=4 + 0.5 х (20 – 4)=12%. \] Таким образом, инвестор ожидает, что инструмент будет приносить доход в размере 12%. Расчет модели CAPM в Excel Приведем пример расчета модели CAMP с использованием редактора Excel. Исходные данные будут такие:
Коэффициент β посчитан способом линейной регрессии между доходностями по акциям Tesla и индексу NASDAQ и составляет 3,17. Как мы помним, значение больше единицы указывает на то, что акции чувствительны к изменению рыночной доходности. \[ RE=Rf + β х (Rm – Rf)=1,51\% + 3,17 х (3,46\% – 1,51\%)=7,69\%. \] Ожидаемая доходность выше ставки по безрисковым бумагам и значительно выше рыночной доходности Rm, которая рассчитана как среднее значение по индексу NASDAQ. Как устроена модель CAPMМодель ценообразования на капитальные активы предполагает следующее:
Как можно использовать модель CAPMБазовая модель оценки капитальных активов соответствует критерию определения цены капитала: сумма ожидаемой прибыли деленная на количество ценных бумаг. Ожидаемая доходность рассчитывается с учетом рисков и чувствительности цены к изменениям общей ситуации на рынке. Модель CAPM исходит из того, что инвесторы могут варьировать структуру портфеля с учетом премии за риск. В свою очередь, финансовые менеджеры используют модель для расчета стоимости капитала компании. Где применяется модель CAPM Итак, основные задачи CAPM – определение цены капитала и премии за риск. В связи с этим модель можно использовать при расчете ставки дисконтирования. Области применения могут быть самые разные.
Преимущества и недостатки модели CAPMПеречислим плюсы использования модели:
Недостатки модели оценки капитальных активов заключаются в следующем:
Пример расчетаИтак, модель оценки капитальных активов включает следующие компоненты:
Рассмотрим простой пример расчета ставки дохода на собственный капитал (RE) по модели CAPM с использованием исходных данных: \( Rf \) =5% (ставка по ОФЗ); Сначала рассчитаем премию за риск: \[ RE=0,05 + 1,5 х 0,07=0,155 \] Таким образом, ставка дохода на собственный капитал составляет 15,5%. ЗаключениеБазовая модель ценообразования на капитальные активы используется для оценки степени влияния риска на будущую доходность ценных бумаг. Применение CAPM в условиях кризисов может давать недостоверные результаты ввиду высокой волатильности рынка: возникает необходимость постоянно пересчитывать премию за риск, которая меняется практически каждый день. Ориентированная на долгосрочную перспективу, модель CAPM не подходит для такой ситуации. Как и любой другой инструмент расчета, модель оценки активов CAPM следует использовать в совокупности с другими методиками: WACC (средневзвешенная стоимость капитала), DDM (модель дисконтирования дивидендов) и др. Источник Модель доходности финансовых активов (САPМ).Модель (САPМ) описывает зависимость между рыночным риском и требуемой доходностью. Модель (САPМ) основывается на системе строгих предпосылок [16].Cогласно логике этой модели, инвестиционное решение принимается под воздействием двух факторов — ожидаемой доходности Формальная запись итогового уравнения данной модели выглядит следующим образом: где mf — ставка дохода на безрисковую ценную бумагу, которые являются важнейшим элементом фондового рынка. примером гарантированных ценных бумаг с фиксированным доходом являются, например, государственные облигации. bi — коэффициент акции i (bi) – это мера рыночного риска акции. Он измеряет изменчивость доходности акции по отношению к доходности среднерыночного портфеля. b -коэффициент связан с наклоном характеристической линии акции, представляющей собой графическое изображение уравнения регрессии, построенного по статистическим данным о доходности i-й акции и среднерыночной доходности. b -коэффициент связан с наклоном характеристической линии акции, представляющей собой графическое изображение уравнения регрессии, построенного по статистическим данным о доходности i-й акции и среднерыночной доходности. ( Связь между доходом ценной бумаги и ее бета — коэффициентом линейная и называется линией рынка ценных бумаг (Security Market Line — SML).Уравнение SML может быть записано в форме: На графике SML по горизонтальной оси отложены коэффициенты β, по вертикальной — эффективности бумаг или портфелей. Но эта прямая SML отражает идеальную зависимость между β и эффективностью бумаг и портфелей. Все точки, лежащие на прямой SML, соответствуют «справедливо» оцененным бумагам (портфелям), а те, которые лежат выше /ниже этой линии, — недооцененным/переоцененным. Графическое изображение линии рынка ценных бумаг для примера 4.3. приведено на рисунке 4.7. Линия рынка ценных (SML) бумаг отражает зависимость риск – доходность для отдельных акций. Требуемая доходность любой акции равна безрисковой норме, сложенной с произведением премии за рыночный риск и b — коэффициента акции: Отсутствие риска по безрисковым ценным бумагам влечет за собой и минимальный уровень прибыли. В силу этого безрисковые бумаги являются главным регулятором прибылей и рисков. Предположим, что значение доходности по гарантированным бумагам составляет величину mf. В этом случае любой инвестиционный портфель, имеющий бумаги с той или иной степенью риска, дает более высокую прибыль, чем аналогичные по объему инвестиции в гарантированные бумаги. Следовательно, можно заключить, что замена любых ценных бумаг на более прибыльные повышает риск портфеля. Эффективность ценных бумаг удобно отсчитывать от эффективности безрискового вклада mf. Превышение эффективности ценной бумаги над безрисковой эффективностью mf называется премией за риск. Таким образом, эта премия за риск в основном линейно зависит от премии за риск, складывающейся для рынка в целом, и коэффициентом является «бета» данной бумаги. Это, однако, верно, если a=0. Такие ценные бумаги называются «справедливо» оцененными. Те же бумаги, у которых a > 0, рынком недооценены, a если a Однако российские государственные обязательства вовсе не являются безрисковыми. Это было очевидно задолго до кризиса 1998 г.: доходность ГКО всегда была изменчивой и то поднималась (в период их обращения) до 200% годовых и выше, то опускалась (во время относительной стабилизации экономической ситуации) до 15%. Если мерой риска является дисперсия, то можно сказать однозначно, что ГКО были не просто рисковыми, а чисто спекулятивными бумагами. Неочевидным для развивающихся рынков также является вопрос: какой должна быть рыночная премия к доходности, т.е. величина ( Здесь скрываются две проблемы. Во-первых, если эту премию определить на основе какого-либо существующего российского биржевого индекса, то мы рискуем опереться на недостоверные данные. На российском фондовом рынке преобладает внебиржевая активность, и, как показывают отдельные исследования, он обладает низкой степенью информационной эффективности. Это может привести к тому, что индекс, основанный на усредненных котировках спроса и предложениях внебиржевых трейдеров, исказит действительные тенденции, существующие на рынке. Во-вторых, если даже принять за основу наиболее достойный доверия фондовый индекс и считать его достаточно надежным индикатором динамики рыночного портфеля, то остро ощущается недостаток информации. Выводя свои среднерыночные премии, Э. Димсон основывался на анализе предыстории длиной в 50 лет. Однако развивающийся рынок, как правило, молодой и нестабильный. Период нестабильности губителен для инвестиционной активности и не должен продолжаться долго. Поэтому тренд развивающегося рынка: неопределенный в связи с малой глубиной предыстории и общей волатильностью; неоднородный, поскольку правительство развивающейся страны будет стараться привлечь инвесторов, стабилизировать рынок и повысить его предсказуемость. На этом пути оно будет пробовать разные стратегии, что отразится на динамике фондового рынка. Например, взяв за основу расчета интервал времени 1995-1997 гг. по рынку России, мы получим среднегодовой уровень доходности около 80% (в долларах). Совершенно понятно, что мы не можем требовать такой доходности от долгосрочных проектов промышленных корпораций, это сделало бы большинство хороших и реальных проектов в Российской Федерации нерентабельными, и поэтому расчет такого рода был бы некорректен. Линия рынка капитала (CML) отражает зависимость риск – доходность для эффективных портфелей,т. е. для портфелей, сочетающих рисковые и безрисковые активы. Заметим, что не только бумаги имеют «беты», но также и портфели, и «бета» портфеля равна взвешенной сумме «бета» бумаг, входящих в портфель. Как и для бумаг, портфель называется «справедливо» оцененным, недооцененным или переоцененным в зависимости от ap. Из сказанного вытекает соотношение, известное под названием линии рынка капитала (CML), связывающее показатели эффективности и степень риска портфеля, т. е. mр и mp= mf + где mp — доходность (эффективность) портфеля акций; mf — доходность безрисковых ценных бумаг; sp — СКО доходности акций портфеля. Рассмотрим два утверждения о риске ценной бумаги и портфельном риске: · Рыночный риск принимает во внимание большую часть хорошо диверсифицированного портфеля. · Бета отдельной бумаги измеряет ее чувствительность к колебаниям рынка. Попытаемся объяснить это. Предположим, что мы получили портфель, содержащий большое число ценных бумаг, скажем, 100, путем случайного выбора их на рынке. Что мы тогда будем иметь? Сам рынок, или портфель очень близкий к рынку. Бета портфеля будет равна 1, и корреляция с рынком будет равна 1. Если стандартное отклонение на рынке равно 20%, то и стандартное отклонение портфеля будет 20%. Предположим теперь, что мы получили портфель из большой группы бумаг со средней бетой 1.5. И этот портфель будет жестко связан с рынком. Однако, его стандартное отклонение будет 30%, в 1.5 раза больше, чем у рынка. Хорошо диверсифицированный портфель с бетой 1.5 будет усиливать каждое движение рынка на 50% и будет иметь 150% от рыночного риска. Конечно, то же самое можно повторить с бумагами с бетой 0.5 и получить хорошо диверсифицированный портфель, вдвое менее рисковый, чем рынок. Общее утверждение таково: риск хорошо диверсифицированного портфеля пропорционален бете портфеля, которая равна средней бете бумаг, включенных в этот портфель. Это показывает, как портфельный риск определяется бетами отдельных бумаг. Величины коэффициентов «бета» в модели САРМ ив рыночной модели сходны по смыслу. Однако в отличие от САРМ рыночная модель не является моделью равновесия финансового рынка. Более того, рыночная модель использует рыночный индекс, который в общем случае не охватывает рыночный портфель, используемый в САРМ. Существует ряд причин, по которым требуемая и ожидаемая доходности не совпадают. В их числе: 1) изменение безрисковой ставки ввиду пересмотра ожидаемого темпа инфляции, 2) изменение b; 3) переоценка отношения инвеcтopa к риску. САРМ хорошо обоснована с позиции теории, однако она не может быть подтверждена эмпирически, ее параметры с трудом поддаются оценке. Поэтому применение САРМ на практике ограничено. Для того, чтобы она “работала” необходимо соблюдение таких заведомо нереалистических условий как наличие абсолютно эффективного рынка, отсутствие транзакционных издержек и налогов, равный доступ всех инвесторов к кредитным ресурсам и др. Тем не менее столь абстрактное логическое построение получило практически всеобщее признание в мире реальных финансов. Крупнейшие рыночные институты, такие как инвестиционный банк Merril Lynch, регулярно рассчитывают β — коэффициенты всех крупных компаний, котирующихся на фондовых биржах. Отсутствие в России сформированной финансовой инфраструктуры пока еще препятствует использованию всего потенциала, заложенного в данную модель. Поэтому рассмотрим пример расчета уровня ожидаемой доходности с использованием подхода capm на фондовом рынке сша. Компания, имеющая β — коэффициент 2.5, собирается привлечь дополнительный собственный капитал путем эмиссии обыкновенных акций. Уровень безрисковой процентной ставки составляет 6.25%, средняя доходность рынка, рассчитанная по индексу S&P 500, – 14%. Для того, чтобы сделать свои ценные бумаги привлекательными для инвесторов, компания должна предложить по ним ежегодный доход не ниже 25.625% (6.25 + 2,5 * (14 – 6.25)). Размер премии за риск составит 19.375%. Столь существенные ограничения, накладываемые рынком на возможности снижения цены капитала, устанавливают предел доходности инвестиционных проектов, которые компания собиралась финансировать привлекаемым капиталом: внутренняя норма доходности этих проектов должна быть не ниже 25.625%. В противном случае NPV проектов окажется отрицательной, то есть они не обеспечат увеличения стоимости предприятия. Если бы β-коэффициент компании был равен 1.5, то размер премии за риск составил бы 11.625% (1,5 * (14 – 6.25)), то есть цена нового капитала составила бы лишь 17.875%.
Рисунок. Взаимосвязь уровня β — коэффициента и требуемой доходности С целью преодоления отмеченных недостатков САРМ были предприняты попытки разработки альтернативных моделей риск – доходность; теория арби-тражного ценообразования (АРТ) – наиболее перспективная из новых моделей. Пример 4.3. В таблице приведена информация о доходности акции GLSYTr (mi) и индекс рынка (mr) на протяжении десяти кварталов:
Известно, что эффективность безрисковых вложений равна 4%. (рыночная модель, Модель доходности финансовых активов (САМР), Линия рынка ценных (SML) бумаг). Требуется: 1) построить рыночную модель, где mi – зависимая переменная, mr — объясняющая переменная; 2) определить характеристики ценной бумаги: рыночный (или систематический) риск, собственный(или несистематический) риск, R 2 , a. 3) привести график построенной модели; 4) построить линию рынка ценных бумаг (SML). Решение 1)Параметры модели найдем с помощью инструмента Регрессия Пакет анализа[13]EXCEL. 1. Ввод данных (рис. 4.4. – 4.5.). Рис. 4.4. Регрессия — выбор инструмента анализа. Рис. 4.5. Заданы интервалы входных данных. 2. Результаты расчетов (табл. 4.3 –4.5).
Используя данные таблицы 4.3, полученную рыночную модель можно записать в виде mi = 4.667 + 1.833 ´mr. Следовательно, b- коэффициент акции GLSYTr равен 1.833. Пояснения для вычислений без ПЭВМ. b i = где · Для вычисления собственного риска
Пояснения к таблице 4.
· Для вычисления систематического риска (или рыночного) необходимо сначала вычислить bi 2 = 1.833*1.833=3.36, а теперь можно определить величину рыночного риска: bi 2 smr 2 = 3.36*1.2= 4.03. · R-squared равен 0.840(из табл. 5) Пояснения для вычислений без ПЭВМ. Ri 2 =bi 2 smr 2 / Это отношение характеризует долю риска данных ценных бумаг, вносимую рынком. поведение акций компании GLSYTr на 84% предсказуемо с помощью индекса рынка.
акции компании GLSYTr можно отнести к классу «агрессивных» ценных бумаг, т. к. бета – коэффициент равен 1.833. · График регрессионной модели зависимости доходности акций GLSYTr от индекса рынка приведен на рис. 8. 3) График регрессионной модели зависимости доходности акций GLSYTr от индекса рынка приведен на рисунке 4.6. 4.4 Многофакторные модели. Теория арбитражного ценообразования. В факторных (или индексных)моделях (factor models) предполагается, что доходность ценной бумаги реагирует на изменения различных факторов (или индексов). САРМ представляет собой однофакторную модель. Это означает, что риск является функцией одного фактора – b — коэффициента, выражающего зависимость между доходностью ценной бумаги и доходностью рынка. На самом деле, зависимость между риском и доходностью более сложная. В этом случае можно предположить, что требуемая доходность акции будет функцией более чем одного фактора. Более того, не исключено, что зависимость между риском и доходностью является многофакторной. Стивен Росс предложил метод, названный теорией арбитражного ценообразования (Arbitrage Pricing Theory, АРТ). Концепция АРТ предусматривает возможность включения любого количества факторов риска, так что требуемая доходность может быть функцией трех, четырех ил даже большего числа факторов. для того чтобы точно оценить ожидаемые доходности, дисперсии и ковариации ценных бумаг многофакторные модели более полезны, чем рыночная модель. Это объясняется тем, что фактические доходности по ценным бумагам оказываются чувствительными не только к изменению индекса рынка, и в экономике существует более одного фактора, влияющего на доходность ценных бумаг. Можно выделить несколько факторов, оказывающих влияние на все сферы экономики: 1. Темпы прироста валового внутреннего продукта. 2. Уровень процентных ставок. 3. Уровень инфляции. 4. Уровень цен на нефть. При построении многофакторных моделей пытаются учесть основные экономические факторы, систематически воздействующие на курсовую стоимость всех ценных бумаг. на практике все инвесторы явно или неявно применяют факторные модели. Это связано с тем, что невозможно рассматривать взаимосвязь каждой ценной бумаги с каждой другой по отдельности, так как объем вычислений при расчете ковариаций ценных бумаг растет с ростом числа анализируемых ценных бумаг. Если принять, что доходности ценных бумаг подвержены влиянию одного или более факторов, то первоначальной целью анализа ценных бумаг является определение этих факторов и чувствительности доходностей ценных бумаг к их изменению. В отличие от однофакторных моделей многофакторная модель доходности ценных бумаг, учитывающая эти различные воздействия, может быть более точной. · Наибольшей известностью пользуется многофакторная модель BARRA, которая была разработана в 1970-х г. Барром Розенбергом и с тех пор постоянно усовершенствуется. При этом кроме рыночных показателей при разработке BARRA учитывались финансовые показатели (в частности, данные баланса) компаний. Новая версия BARRA, так называемая Е2, использует 68 различных фундаментальных и промышленных факторов. Хотя первоначально BARRA предназначалась для оценки американских компаний, практика показала, что она с успехом может применяться и в других странах. · Другой разновидностью многофакторных моделей является модель арбитражного ценообразования АРТ Стефана Росса (1976). АРТ является двухуровневой моделью. Сначала определяются чувствительности к заранее выбранным факторам, а затем строится многофакторная модель, в которой роль факторов играют доходности по портфелям, имеющим единичную чувствительность к одному из факторов и нулевую чувствительность ко всем остальным. Модель аналога линии SML в арбитражной теории выглядит следующим образом: где Недостатком данной модели является следующее: на практике трудно выяснить, какие конкретные факторы риска нужно включать в модель. В настоящее время в качестве таких факторов используют показатели: развития промышленного производства, изменений уровня банковских процентов, инфляции, риска неплатежеспособности конкретного предприятия и т.д. Рассмотрев основные вопросы, относящиеся к вычислению процентного риска, можно подвести некоторые итоги. Рынок ценных бумаг делится на множество различных групп с различными уровнями дохода и риска, причем обычно зависимость между этими величинами прямая (заметим, что в случае обратной зависимости будет наблюдаться господство самой доходной и безопасной бумаги, как было с ГКО). Увеличенная доходность является своего рода премией за риск. Таким образом, инвестору приходится выбирать между риском и доходностью. Источник |



 и риска, мерой которого является дисперсия или стандартное отклонение доходности. Приняв ряд допущений (инвесторы ведут себя рационально, измеряют время в одних единицах, мыслят сходным образом, заимствуют и предоставляют средства в долг под безрисковую ставку и др.), авторы модели показали, что при соблюдении указанных допущений инвестиционный портфель, повторяющий пропорции рынка, должен быть оптимальным инвестиционным решением для всех инвесторов.
и риска, мерой которого является дисперсия или стандартное отклонение доходности. Приняв ряд допущений (инвесторы ведут себя рационально, измеряют время в одних единицах, мыслят сходным образом, заимствуют и предоставляют средства в долг под безрисковую ставку и др.), авторы модели показали, что при соблюдении указанных допущений инвестиционный портфель, повторяющий пропорции рынка, должен быть оптимальным инвестиционным решением для всех инвесторов.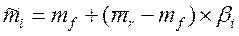 , (4.9)
, (4.9) ) -рыночная премия за риск.
) -рыночная премия за риск.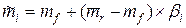
 (mp £
(mp £ 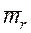 , sp £ smr )
, sp £ smr ) ´
´  ,
,  (4.10)
(4.10) — СКО доходности рыночных ценных бумаг;
— СКО доходности рыночных ценных бумаг;







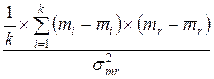 =2.2/1.2=1.833,
=2.2/1.2=1.833, 230/10=23,
230/10=23,  =100/10=10,
=100/10=10, = 1.2,
= 1.2,  =2.2
=2.2 воспользуемся формулой
воспользуемся формулой  .
.


 = 4.03/4.8=0.84
= 4.03/4.8=0.84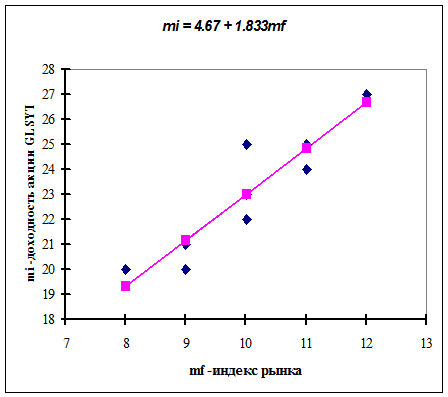

 ,
, — требуемая доходность портфеля с единичной чувствительностью к j –му экономическому фактору
— требуемая доходность портфеля с единичной чувствительностью к j –му экономическому фактору 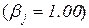 и нулевой чувствительностью
и нулевой чувствительностью  к другим факторам.
к другим факторам.