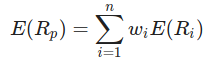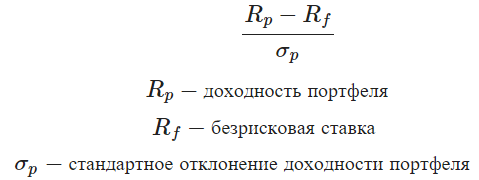Модель портфеля максимальной доходности

Оптимизации портфеля с помощью Python и PyPortfolioOpt

Портфельная теория Марковица(далее ПТМ) (Modern portfolio theory) — разработанная Гарри Марковицем методика формирования инвестиционного портфеля, направленная на оптимальный выбор активов, исходя из требуемого соотношения доходность/риск. Сформулированные им в 1950-х годах идеи составляют основу современной портфельной теории.

Основные положения портфельной теории были сформулированы Гарри Марковицем при подготовке им докторской диссертации в 1950—1951 годах.

Рождением же портфельной теории Марковица считается опубликованная в «Финансовом журнале» в 1952 году статья «Выбор портфеля». В ней он впервые предложил математическую модель формирования оптимального портфеля и привёл методы построения портфелей при определённых условиях. Основная заслуга Марковица состояла в предложении вероятностной формализации понятий «доходность» и «риск», что позволило перевести задачу выбора оптимального портфеля на формальный математический язык. Надо отметить, что в годы создания теории Марковиц работал в RAND Corp., вместе с одним из основателей линейной и нелинейной оптимизации — Джорджем Данцигом и сам участвовал в решении указанных задач. Поэтому собственная теория, после необходимой формализации, хорошо ложилась в указанное русло.

Марковиц постоянно занимается усовершенствованием своей теории и в 1959 году выпускает первую посвящённую ей монографию «Выбор портфеля: эффективная диверсификация инвестиций».

В 1990 году, когда Марковицу вручают Нобелевскую премию, выходит книга «Средне-дисперсионный анализ при выборе портфеля и рынка капитала» ссылка.

Основа модели

1. Ожидаемая доходность портфеля(Portfolio Expected Return)

Ожидаемая доходность портфеля будет зависеть от ожидаемой доходности каждого из активов, входящих в него. Такой подход позволяет снизить риск за счет диверсификации и одновременно максимизировать доход инвестора, поскольку убытки по одним инвестициям будут компенсированы доходом по другим.

Ожидаемая доходность портфеля представляет собой суммарную ожидаемую доходность входящих в него ценных бумаг, взвешенную с учетом их доли в портфеле.

2. Дисперсия портфеля (Portfolio Variance)

Дисперсия портфеля — это процесс, который определяет степень риска или волатильности, связанной с инвестиционным портфелем. Основная формула для расчета этой дисперсии фокусируется на взаимосвязи между так называемой дисперсией доходности и ковариацией, связанной с каждой из ценных бумаг, найденных в портфеле, а также с процентом или частью портфеля, который представляет каждая ценная бумага.

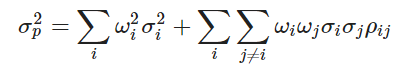
3. Коэффициент Шарпа (Sharpe Ratio)

Коэффициент Шарпа измеряет доходность инвестиций по отношению к безрисковой ставке (казначейской ставке) и степени риска. В целом, более высокое значение коэффициента Шарпа указывает на лучшие и более прибыльные инвестиции. Таким образом, если сравнивать два портфеля с одинаковыми рисками, то при прочих равных условиях было бы лучше инвестировать в портфель с более высоким коэффициентом Шарпа.

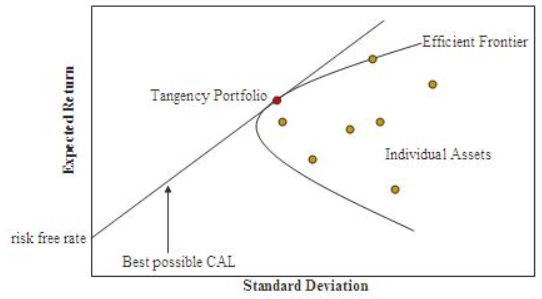
4. Эффективная граница (The Efficient Frontier)

Определение и рисунок из Википедии:

Граница эффективности (англ. Efficient frontier) в портфельной теории Марковица — инвестиционный портфель, оптимизированный в отношении риска и доходности. Формально границей эффективности является набор портфелей, удовлетворяющих такому условию, что не существует другого портфеля с более высокой ожидаемой доходностью, но с таким же стандартным отклонением доходности. Понятие границы эффективности было впервые сформулировано Гарри Марковицем в 1952 году в модели Марковица.

Портфель может быть охарактеризован как «эффективный», если он имеет максимально возможный ожидаемый уровень доходности для своего уровня риска (который представлен стандартным отклонением доходности портфеля). Так, на график соотношения риска и доходности может быть нанесена любая возможная комбинация рискованных активов, и совокупность всех таких возможных портфелей определяет регион в этом пространстве. При отсутствии в портфеле безрискового актива граница эффективности определяется верхней (восходящей) частью гиперболы, ограничивающей область допустимых решений для всех соотношений активов в портфеле.

В случае же, если в портфель может быть включён безрисковый актив, граница эффективности вырождается в отрезок прямой линии, исходящий от значения доходности безрискового актива на оси ординат (ожидаемая доходность портфеля) и проходящий по касательной к границе области допустимых решений. Все портфели на отрезке между собственно безрисковым активом и точкой касания состоят из комбинации безрискового актива и рисковых активов, в то время как все портфели на линии выше и справа от точки касания образуются короткой позицией в безрисковом активе и инвестированием в рисковые активы.

Оптимизация портфеля на Python

1. Импорт необходимых библиотек

2. Получение данных по акциям из интернета

Сначала установим опять пакет, который не входит в стандартный набор. Он позволяет получить данные по акциям с сайта yahoo.

Тикеры, которые будут использоваться для анализа — одна из компаний входящих в лидеры в своем секторе.

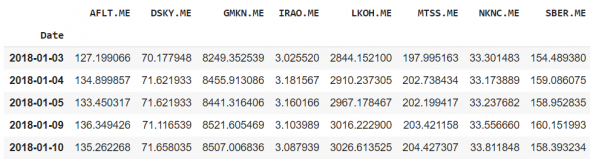
Дальше необходимо проверить есть ли среди полученных значений NaN. В случае их наличия они будут мешать дальнейшему исследованию. Для того, чтобы это решить, необходимо рассмотреть или иную акцию, или заменить их для примера средней ценой между днем до и после значения NaN.

3. Расчеты

Перейдем к расчетам по оптимизации портфеля и начнем с определения ожидаемой доходности и дисперсии портфеля. Далее сохраним значения весов портфеля с максимальным коэффициентом Шарпа и минимальной дисперсией.

OrderedDict([(‘AFLT.ME’, 0.0), (‘DSKY.ME’, 0.22606), (‘GMKN.ME’, 0.48796), (‘IRAO.ME’, 0.0), (‘LKOH.ME’, 0.0), (‘MTSS.ME’, 0.02953), (‘NKNC.ME’, 0.25645), (‘SBER.ME’, 0.0)])

Необходимо обратить внимание, что если изменить weight_bounds=(0,1) на weight_bounds=(-1,1), то в портфеле будут учитываться и короткие позиции по акциям.

Дальше посмотрим общие характеристики по портфелю.

Expected annual return: 37.1%
Annual volatility: 20.7%
Sharpe Ratio: 1.70
(0.37123023494063007, 0.20717177784552962, 1.695357536597058)

Теперь посмотрим портфель с минимальной волатильностью:

OrderedDict([(‘AFLT.ME’, 0.02876), (‘DSKY.ME’, 0.24503), (‘GMKN.ME’, 0.10403), (‘IRAO.ME’, 0.0938), (‘LKOH.ME’, 0.01168), (‘MTSS.ME’, 0.41967), (‘NKNC.ME’, 0.09704), (‘SBER.ME’, 0.0)])

Expected annual return: 24.0%Annual volatility: 16.9%Sharpe Ratio: -0.18(0.239915644698749, 0.16885732511472468, -0.17816434839774456)

4. Построение графика эффективных границ

Заключительным шагом является построение эффективной границы для визуального представления и расчет распределения активов.

Анализ произведем для суммы в 100 000 рублей.

Первым этапом посчитаем портфель с минимальной волатильностью:
<'AFLT.ME': 41, 'DSKY.ME': 181, 'IRAO.ME': 1765, 'LKOH.ME': 1, 'MTSS.ME': 127, 'NKNC.ME': 107>Осталось денежных средств после построения портфеля с минимальной волатильностью составляет 6152.03 рублей

Вторым шагом портфель с максимальным коэффициентом Шарпа:

<'DSKY.ME': 167, 'GMKN.ME': 2, 'MTSS.ME': 9, 'NKNC.ME': 283>Leftover Fund value in$ after building Max Sharpe ratio portfolio is $1319.05 Осталось денежных средств после построения портфеля с максимальным коэффициентом Шарпа 1319.05 рублей

В результате нам предлагается купить для оптимального портфеля 167 акций Детского мира, 2 акции Норильского никеля, 9 акций МТС и 283 акцию Нижнекамскнефтехим. В результате у нас еще останется 1319 рублей.

Еще раз напоминаю, что все вышеприведённое не является инвестиционной рекомендацией, а только поводом к размышлению.

Источник

Составление инвестиционного портфеля по Марковицу

В данном обзоре мы представим простой пример составления оптимального инвестиционного портфеля по Марковицу.

Введение в портфельную теорию

Портфельная теория Марковица была обнародована в 1952 году. Позже автор получил за нее Нобелевскую премию.

Целью модели является составление оптимального портфеля, то есть с минимальным риском и максимальной доходностью.

Как правило, решается две задачи: максимизация доходности при заданном уровне риска и минимизация риска при минимально допустимом значении доходности.

Доходность портфеля измеряется как средневзвешенная сумма доходностей входящих в него бумаг.

wi – доля инструмента в портфеле;

ri – доходность инструмента.

Риск отдельного инструмента оценивается как среднеквадратичное (стандартное) отклонение его доходности. Для расчета общего риска портфеля необходимо отразить совокупное изменение рисков отдельного инструмента и их взаимное влияние (через ковариации и корреляции – меры взаимосвязи).

σi – стандартное отклонение доходностей инструмента;

kij – коэффициент корреляции между I,j-м инструментом;

Vij – ковариация доходностей i-го и j-го финансового инструмента;

n – количество финансовых инструментов в рамках портфеля.

Таким образом, в рамках правильно подобранного портфеля риски снижаются за счет обратной корреляции инструментов. При этом устраняются не только специфические риски инструмента, но и снижается систематический (рыночный) риск.

Для составления портфеля решается оптимизационная задача. При этом в базовом виде использование заемных средств не предполагается, то есть сумма долей активов равняется единице, а доли эти положительны.

Минимизируем риск при минимально допустимом уровне доходности

Максимизируем доходность при заданном уровне риска

Пример расчетов в Excel

Оптимальный портфель содержит различные группы активов – акции, облигации, товарные фьючерсы и т.д. Так легче подобрать инструменты с отрицательной корреляцией и минимизировать риски.

В нашем примере будет использован более простой подход – составление портфеля из нескольких американских акций. Для эффекта диверсификации возьмем представителей различных секторов – платежную систему VISA, ритейлера Macy’s, технологичного гиганта Apple и телеком AT&T.

Сразу отмечу, что это лишь пример. Все эмитенты интересны, но для грамотного составления портфеля необходимо учитывать фундаментальные показатели, включая рыночные мультипликаторы, оценивать технические уровни для входа в позицию.

Этап 1. Выкачиваем котировки. Необходимо взять данные минимум за год. В нашем примере были взяты ежемесячные цены закрытия с 31.06.2017 по 31.05.2018.

Этап 2. Считаем доходности по каждой бумаге. Для простоты не будем учитывать эффект дивидендов.

Считаем доходность за каждый месяц по формуле натурального логарифма. К примеру, доходность VISA за май 2018 = LN(C14/C13)

Для расчета ожидаемой доходности берем среднее значение за рассматриваемый период. В нашем случае это год. Ожидаемая доходность VISA = СРЗНАЧ(G3:G14)

Получаем отрицательную доходность AT&T, и убираем бумагу из портфеля. Сразу отмечу, что в этом заключается недостаток модели, ведь просевшие ранее акции в перспективе могут развернуться.

Этап 3. Расчет риска каждой акции. Производится по формуле стандартного отклонения. К примеру, риск VISA =СТАНДОТКЛОН(G3:G14)

Этап 4. Расчет ковариаций между бумагами. Воспользуемся специальной надстройкой в Excel. Для этого выберем в Главном меню → «Данные» → «Анализ данных» → «Ковариация».

Указываем окне входной интервал – ежемесячные доходности акций, а в опции «Группирование» выбираем «по столбцам».

В результате получаем ковариационную матрицу.

Этап 5. Расчет общей доходности портфеля. Для начала установим произвольные доли бумаг в портфеле. Они положительны, их сумма равна 1.

Считаем средневзвешенное значение доходностей отдельных акций. Воспользуемся формулой G15*G23+H15*H23+I15*I23

Этап 6. Расчет общего риска портфеля. Производится по формуле массива КОРЕНЬ(МУМНОЖ(МУМНОЖ(G23:I23;G20:I22); E20:E22))

Этап 7. Портфель минимального риска.

Речь идет о долях отдельных бумаг в портфеле. Для начала необходимо определить минимальный уровень допустимой доходности портфеля (rp). Возьмем rp >= 3,2%.

При оценке долей акций воспользуемся надстройкой в Excel «Поиск решений», для этого выбираем Главное меню → «Данные» → «Поиск решений».

В надстройке «Поиск решений» необходимо ввести ссылку на ячейку, которую следует оптимизировать (общий риск портфеля, минимизируем), ввести какие параметры необходимо изменять (доли акций) и ограничения. Введем ограничения на весовые значения коэффициентов у акций: сумма долей акций должна быть равна 1 и сами доли должны иметь положительный знак.

В результате имеем портфель с 73% долей VISA и 27% долей Macy’s.

Визуально портфель выглядит так:

Этап 8. Портфель максимальной доходности.

Для начала необходимо определить максимальный уровень допустимого риска портфеля (σp). Возьмем σp Основные виды деятельности: Работа на финансовых рынках Консультирование и сопровождение в работе на финансовых рынках Юридические услуги, связанные с регистрацией, перерегистрацией, ликвидацией российских юридических лиц Консультирование в сфере кредитования и защиты прав заёмщика Информационные услуги связанные с ведением бизнеса

Источник

Составление инвестиционного портфеля по Марковицу для чайников

В данном обзоре мы представим простой пример составления оптимального инвестиционного портфеля по Марковицу.

Введение в портфельную теорию

Портфельная теория Марковица была обнародована в 1952 году. Позже автор получил за нее Нобелевскую премию.

Целью модели является составление оптимального портфеля, то есть с минимальным риском и максимальной доходностью.

Как правило, решается две задачи: максимизация доходности при заданном уровне риска и минимизация риска при минимально допустимом значении доходности.

Доходность портфеля измеряется как средневзвешенная сумма доходностей входящих в него бумаг.

wi — доля инструмента в портфеле;

ri — доходность инструмента.

Риск отдельного инструмента оценивается как среднеквадратичное (стандартное) отклонение его доходности. Для расчета общего риска портфеля необходимо отразить совокупное изменение рисков отдельного инструмента и их взаимное влияние (через ковариации и корреляции — меры взаимосвязи).

σi — стандартное отклонение доходностей инструмента;

kij — коэффициент корреляции между I,j-м инструментом;

Vij — ковариация доходностей i-го и j-го финансового инструмента;

n — количество финансовых инструментов в рамках портфеля.

Таким образом, в рамках правильно подобранного портфеля риски снижаются за счет обратной корреляции инструментов. При этом устраняются не только специфические риски инструмента, но и снижается систематический (рыночный) риск.

Для составления портфеля решается оптимизационная задача. При этом в базовом виде использование заемных средств не предполагается, то есть сумма долей активов равняется единице, а доли эти положительны.

Минимизируем риск при минимально допустимом уровне доходности

Максимизируем доходность при заданном уровне риска

Пример расчетов в Excel

Оптимальный портфель содержит различные группы активов — акции, облигации, товарные фьючерсы и т.д. Так легче подобрать инструменты с отрицательной корреляцией и минимизировать риски.

В нашем примере будет использован более простой подход — составление портфеля из нескольких американских акций. Для эффекта диверсификации возьмем представителей различных секторов — платежную систему VISA, ритейлера Macy’s, технологичного гиганта Apple и телеком AT&T.

Сразу отмечу, что это лишь пример. Все эмитенты интересны, но для грамотного составления портфеля необходимо учитывать фундаментальные показатели, включая рыночные мультипликаторы, оценивать технические уровни для входа в позицию.
Этап 1. Выкачиваем котировки. Необходимо взять данные минимум за год. В нашем примере были взяты ежемесячные цены закрытия с 31.06.2017 по 31.05.2018.
Этап 2. Считаем доходности по каждой бумаге. Для простоты не будем учитывать эффект дивидендов.

Считаем доходность за каждый месяц по формуле натурального логарифма. К примеру, доходность VISA за май 2018 = LN(C14/C13)

Для расчета ожидаемой доходности берем среднее значение за рассматриваемый период. В нашем случае это год. Ожидаемая доходность VISA = СРЗНАЧ(G3:G14)

Получаем отрицательную доходность AT&T, и убираем бумагу из портфеля. Сразу отмечу, что в этом заключается недостаток модели, ведь просевшие ранее акции в перспективе могут развернуться.
Этап 3. Расчет риска каждой акции. Производится по формуле стандартного отклонения. К примеру, риск VISA =СТАНДОТКЛОН(G3:G14)

Указываем окне входной интервал — ежемесячные доходности акций, а в опции «Группирование» выбираем «по столбцам».

В результате получаем ковариационную матрицу.

Этап 5. Расчет общей доходности портфеля. Для начала установим произвольные доли бумаг в портфеле. Они положительны, их сумма равна 1.

Считаем средневзвешенное значение доходностей отдельных акций. Воспользуемся формулой G15*G23+H15*H23+I15*I23

Этап 6. Расчет общего риска портфеля. Производится по формуле массива КОРЕНЬ(МУМНОЖ(МУМНОЖ(G23:I23;G20:I22); E20:E22))

Этап 7. Портфель минимального риска.

Речь идет о долях отдельных бумаг в портфеле. Для начала необходимо определить минимальный уровень допустимой доходности портфеля (rp). Возьмем rp >= 3,2%.

При оценке долей акций воспользуемся надстройкой в Excel «Поиск решений», для этого выбираем Главное меню → «Данные» → «Поиск решений».

В надстройке «Поиск решений» необходимо ввести ссылку на ячейку, которую следует оптимизировать (общий риск портфеля, минимизируем), ввести какие параметры необходимо изменять (доли акций) и ограничения. Введем ограничения на весовые значения коэффициентов у акций: сумма долей акций должна быть равна 1 и сами доли должны иметь положительный знак.

В результате имеем портфель с 73% долей VISA и 27% долей Macy’s.

Визуально портфель выглядит так:

Этап 8. Портфель максимальной доходности.

Для начала необходимо определить максимальный уровень допустимого риска портфеля (σp). Возьмем σp 30

Последние новости

Рекомендованные новости

События недели. Главное с БКС Экспресс

Итоги торгов. Удерживаться на рекордных уровнях становится все труднее

Анализ эмитента. Intel — ведущий производитель процессоров

Американские коммунальщики. Отрасль с высокими дивидендами

Адрес для вопросов и предложений по сайту: bcs-express@bcs.ru

Copyright © 2008–2021. ООО «Компания БКС» . г. Москва, Проспект Мира, д. 69, стр. 1
Все права защищены. Любое использование материалов сайта без разрешения запрещено.
Лицензия на осуществление брокерской деятельности № 154-04434-100000 , выдана ФКЦБ РФ 10.01.2001 г.

Данные являются биржевой информацией, обладателем (собственником) которой является ПАО Московская Биржа. Распространение, трансляция или иное предоставление биржевой информации третьим лицам возможно исключительно в порядке и на условиях, предусмотренных порядком использования биржевой информации, предоставляемой ОАО Московская Биржа. ООО «Компания Брокеркредитсервис» , лицензия № 154-04434-100000 от 10.01.2001 на осуществление брокерской деятельности. Выдана ФСФР. Без ограничения срока действия.

* Материалы, представленные в данном разделе, не являются индивидуальными инвестиционными рекомендациями. Финансовые инструменты либо операции, упомянутые в данном разделе, могут не подходить Вам, не соответствовать Вашему инвестиционному профилю, финансовому положению, опыту инвестиций, знаниям, инвестиционным целям, отношению к риску и доходности. Определение соответствия финансового инструмента либо операции инвестиционным целям, инвестиционному горизонту и толерантности к риску является задачей инвестора. ООО «Компания БКС» не несет ответственности за возможные убытки инвестора в случае совершения операций, либо инвестирования в финансовые инструменты, упомянутые в данном разделе.

Информация не может рассматриваться как публичная оферта, предложение или приглашение приобрести, или продать какие-либо ценные бумаги, иные финансовые инструменты, совершить с ними сделки. Информация не может рассматриваться в качестве гарантий или обещаний в будущем доходности вложений, уровня риска, размера издержек, безубыточности инвестиций. Результат инвестирования в прошлом не определяет дохода в будущем. Не является рекламой ценных бумаг. Перед принятием инвестиционного решения Инвестору необходимо самостоятельно оценить экономические риски и выгоды, налоговые, юридические, бухгалтерские последствия заключения сделки, свою готовность и возможность принять такие риски. Клиент также несет расходы на оплату брокерских и депозитарных услуг, подачи поручений по телефону, иные расходы, подлежащие оплате клиентом. Полный список тарифов ООО «Компания БКС» приведен в приложении № 11 к Регламенту оказания услуг на рынке ценных бумаг ООО «Компания БКС». Перед совершением сделок вам также необходимо ознакомиться с: уведомлением о рисках, связанных с осуществлением операций на рынке ценных бумаг; информацией о рисках клиента, связанных с совершением сделок с неполным покрытием, возникновением непокрытых позиций, временно непокрытых позиций; заявлением, раскрывающим риски, связанные с проведением операций на рынке фьючерсных контрактов, форвардных контрактов и опционов; декларацией о рисках, связанных с приобретением иностранных ценных бумаг.

Приведенная информация и мнения составлены на основе публичных источников, которые признаны надежными, однако за достоверность предоставленной информации ООО «Компания БКС» ответственности не несёт. Приведенная информация и мнения формируются различными экспертами, в том числе независимыми, и мнение по одной и той же ситуации может кардинально различаться даже среди экспертов БКС. Принимая во внимание вышесказанное, не следует полагаться исключительно на представленные материалы в ущерб проведению независимого анализа. ООО «Компания БКС» и её аффилированные лица и сотрудники не несут ответственности за использование данной информации, за прямой или косвенный ущерб, наступивший вследствие использования данной информации, а также за ее достоверность.

Источник