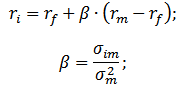- Модель CAPM – что это простыми словами, пример расчета
- Что такое модель CAPM
- Для чего необходима модель оценки капитальных активов
- Формула расчета
- Расчет модели CAPM в Excel
- Как устроена модель CAPM
- Как можно использовать модель CAPM
- Где применяется модель CAPM
- Преимущества и недостатки модели CAPM
- Пример расчета
- Заключение
- Модель оценки капитальных активов – CAPM (У. Шарпа) в Excel
- Модель CAPM. Формула расчета
- Расчет модели CAPM в Excel
- Расчет коэффициента бета с помощью формул Excel
- Расчет коэффициента бета через надстройку «Регрессия»
- Что показывает коэффициент бета в модели CAPM?
Модель CAPM – что это простыми словами, пример расчета
CAPM (Capital Asset Pricing Model) – одна из методик оценки стоимости активов акционерного общества с точки зрения рисков, присущих как непосредственно оцениваемому активу, так и рынку в целом.
Модель CAPM построена на предположении: инвесторы заинтересованы в получении дохода выше, чем доход по безрисковым активам.
CAPM – это метод, который может применяться в теории, на практике его использование возможно лишь в некоторых случаях, в комбинации с другими методиками.
Сегодня мы рассмотрим модель оценки капитальных активов CAPM: формулу расчета этого показателя, его применение на практике, преимущества и недостатки.
Что такое модель CAPM
Как известно, стоимость акционерного общества определяется стоимостью его активов. В данном случае под активами понимают не основные фонды, а финансовые инструменты, эмитентом которых является предприятие.
Предпосылкой CAPM стала гипотеза эффективного рынка капитала, появившаяся в начале XX века. Эта гипотеза основана на том, что рынок является прозрачным, и любые изменения быстро отражаются на стоимости акций. В целом рынок «заточен» на долгосрочные инвестиции.
Современная модель оценки капитальных активов была разработана в середине XX века американским экономистом Гарри Марковицем. Далее метод CAPM был взят на вооружение другими финансовыми гуру: Джоном Линтнером, Джеком Л. Трейнором и Уильямом Шарпом. Последний в 1964 г. разработал модификацию модели, которая используется по сей день. Иногда модель капитальных активов CAPM называют моделью Шарпа.
Итак, на чем основана CAPM model? Попытаемся объяснить простыми словами.
Предположим, есть некий безрисковый актив с минимальной доходностью и практически нулевой волатильностью. Безрисковым средством в модели CAPM обычно выступают государственные облигации. Помимо этого, в портфеле мы имеем акции предприятия нефтедобывающего комплекса. Эти бумаги могут принести неплохой доход, однако уж очень зависят от внешней ситуации, в том числе политической. Какова цель инвестора? Как сбалансировать портфель?
Если наш инвестор очень осторожен, то в его портфеле будут преобладать ОФЗ. Да, он не получит высокий доход, но и ничего не потеряет. А если он все-таки хочет, чтобы его деньги работали и приносили прибыль, то он будет двигаться в сторону увеличения доли бумаг с высокой волатильностью. При этом должно соблюдаться общее правило: если эти бумаги начнут падать и приносить убыток, общая должность портфеля не должна быть ниже, чем ставка доходности по ОФЗ.
Для чего необходима модель оценки капитальных активов
Итак, на чем основана модель оценки капитальных активов? Инвестор должен представлять, какой доход он может получить за то, что рискует своими деньгами.
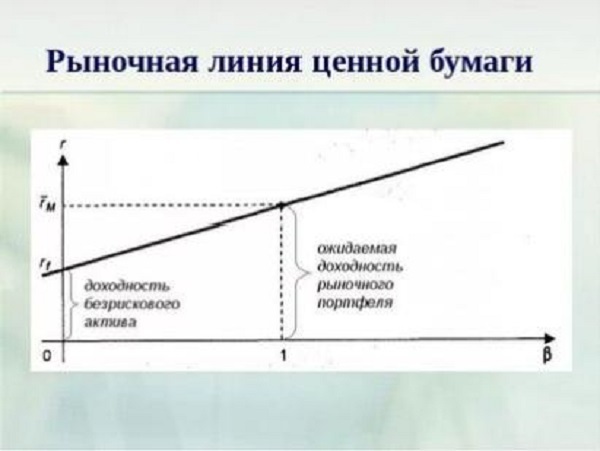
Наглядно CAPM представлена на графике:
Модель CAPM описывает зависимость между доходностью актива, ставкой по безрисковым инструментам и рыночному риску в целом.
CAPM включает элементы:
- доходность безрискового актива;
- ожидаемая общая доходность портфеля;
- общая рыночная доходность;
- чувствительность инструмента к колебаниям рынка (коэффициент β).
Итак, CAPM применяется для оценки доходности ценной бумаги или проекта с учетом систематического (недиверсифицируемого) риска.
Недиверсифицируемый риск – это риск, связанный с отсутствием стабильности в получении дохода. Так, в одном году доходность может быть максимальная, а в следующем периоде оказаться нулевой. Подобные риски присущи ценным бумагам российских компаний, в т.ч. «голубым фишкам».
Возникает резонный вопрос: как рассчитывать или где взять значение коэффициента β? Этот показатель берется из данных статистики. Можно рассчитать коэффициент самостоятельно, используя функции линейной регрессии в Excel, что мы и сделаем в примере ниже. Для этого нужны данные доходности за определенный период по анализируемому активу и в целом по рынку. Для российских бумаг обычно используются индексы РТС или ММВБ, для зарубежных – S&P 500, NASDAQ и др.
Поскольку значения индекса основаны на данных за предыдущие периоды, а само понятие систематического риска говорит о непредсказуемости изменения цены и доходности инструмента, применять расчеты на практике следует с осторожностью. Тем не менее рассчитаем Capital Asset Pricing Model по формуле и в Excel, используя данные по котировкам, находящиеся в свободном доступе.
Формула расчета
Формула CAPM выглядит так:
\[ RE=Rf + β*(Rm – Rf), где: \]
\( RE \) – ожидаемая ставка;
\( Rf \) – ставка по безрисковым инструментам;
\( Rm \) – усредненная прибыль по портфелю в целом;
\( β \) – коэффициент чувствительности актива к колебаниям рынка.
Например, средняя ставка по ОФЗ – 4%. Ожидаемая доходность по портфелю – 20%. Коэффициент β – 0,5.
Приведем таблицу значений β:
| Значение | Комментарий | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| β > 1 | Инструмент чувствителен к колебаниям рынка | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| β = 1 | Доходность актива равна доходности по рынку | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0 Читайте также Реинвестирование: что это простыми словами? Виды, формы и особенности реинвеста \[ RE=4 + 0.5 х (20 – 4)=12%. \] Таким образом, инвестор ожидает, что инструмент будет приносить доход в размере 12%. Расчет модели CAPM в Excel Приведем пример расчета модели CAMP с использованием редактора Excel. Исходные данные будут такие:
Коэффициент β посчитан способом линейной регрессии между доходностями по акциям Tesla и индексу NASDAQ и составляет 3,17. Как мы помним, значение больше единицы указывает на то, что акции чувствительны к изменению рыночной доходности. \[ RE=Rf + β х (Rm – Rf)=1,51\% + 3,17 х (3,46\% – 1,51\%)=7,69\%. \] Ожидаемая доходность выше ставки по безрисковым бумагам и значительно выше рыночной доходности Rm, которая рассчитана как среднее значение по индексу NASDAQ. Как устроена модель CAPMМодель ценообразования на капитальные активы предполагает следующее:
Как можно использовать модель CAPMБазовая модель оценки капитальных активов соответствует критерию определения цены капитала: сумма ожидаемой прибыли деленная на количество ценных бумаг. Ожидаемая доходность рассчитывается с учетом рисков и чувствительности цены к изменениям общей ситуации на рынке. Модель CAPM исходит из того, что инвесторы могут варьировать структуру портфеля с учетом премии за риск. В свою очередь, финансовые менеджеры используют модель для расчета стоимости капитала компании. Где применяется модель CAPM Итак, основные задачи CAPM – определение цены капитала и премии за риск. В связи с этим модель можно использовать при расчете ставки дисконтирования. Области применения могут быть самые разные.
Преимущества и недостатки модели CAPMПеречислим плюсы использования модели:
Недостатки модели оценки капитальных активов заключаются в следующем:
Пример расчетаИтак, модель оценки капитальных активов включает следующие компоненты:
Рассмотрим простой пример расчета ставки дохода на собственный капитал (RE) по модели CAPM с использованием исходных данных: \( Rf \) =5% (ставка по ОФЗ); Сначала рассчитаем премию за риск: \[ RE=0,05 + 1,5 х 0,07=0,155 \] Таким образом, ставка дохода на собственный капитал составляет 15,5%. ЗаключениеБазовая модель ценообразования на капитальные активы используется для оценки степени влияния риска на будущую доходность ценных бумаг. Применение CAPM в условиях кризисов может давать недостоверные результаты ввиду высокой волатильности рынка: возникает необходимость постоянно пересчитывать премию за риск, которая меняется практически каждый день. Ориентированная на долгосрочную перспективу, модель CAPM не подходит для такой ситуации. Как и любой другой инструмент расчета, модель оценки активов CAPM следует использовать в совокупности с другими методиками: WACC (средневзвешенная стоимость капитала), DDM (модель дисконтирования дивидендов) и др. Источник Модель оценки капитальных активов – CAPM (У. Шарпа) в ExcelРассмотрим практические аспекты построения модели оценки капитальных активов CAPM с помощью Excel для отечественных акций ОАО “Газпром”. Модель оценки капитальных активов (англ. Capital Assets Price Model, CAPM) – модель оценки (прогнозирования) будущей доходности актива для инвесторов. Подход оценки активов был теоретически разработана еще в 50-е годы Г.Марковицем, и окончательно сформирован в виде модели в 60-е годы У.Шарпом (1964), Дж. Трейнором (1962), Дж. Линтнером (1965), Ж. Мосином (1966). Модель CAPM основывается на гипотезе эффективного рынка капитала (Efficient Market Hypothesis, EMH), созданной еще в начале 20-го века Л. Башелье и активно продвигаемую Ю.Фамой в 60-е годы. Данная гипотеза имеет ряд условий по способу распространению информации и действию инвесторов на эффективном рынке капитала:
Исходя из гипотезы эффективного рынка, У. Шарп сделал предположение, что на будущую доходность акции будут оказывать влияние только рыночные (системные) риски. Другими словами, будущую доходность акции будут определять общее настроение рынка. Поэтому, кстати, он и был сторонником пассивного инвестирования, когда инвестиционный портфель не пересматривается от получения новой информации. Следует отметить, что на эффективном рынке невозможно получить сверхприбыль. Это делает любое активное управление инвестициями (инвестиционным портфелем) не целесообразным и ставит под сомнение эффективность вложения в ПИФы. В результате, модель У. Шарпа имеет всего один фактор – рыночный риск (коэффициент бета). Анализируя данные постулаты эффективного рынка, можно заметить, что в современной экономике многие из них не выполняются. Модель CAPM в большей степени является теоретической моделью и может использоваться на практике в общем случае.
Модель CAPM. Формула расчетаФормула оценки будущей доходности актива (акции) по модели CAPM имеет следующий аналитический вид: r – ожидаемая доходность актива (акций); rf – доходность по безрисковому активу; rm – среднерыночная доходность; β – коэффициент бета (мера рыночного риска), который отражает чувствительность изменения стоимости активов в зависимости от доходности рынка. Данный коэффициент иногда называют коэффициент Шарпа. Модель представляет собой уравнение линейной регрессии и показывает линейную взаимосвязь между доходностью (r) и рыночным риском (β); σim – стандартное отклонение изменения доходности акции от изменения доходности рынка; σ 2 m – дисперсия рыночной доходности.
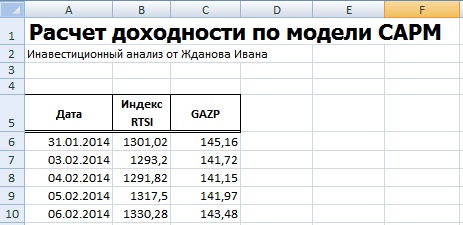
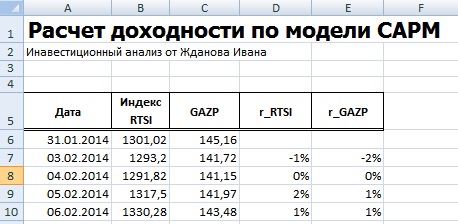
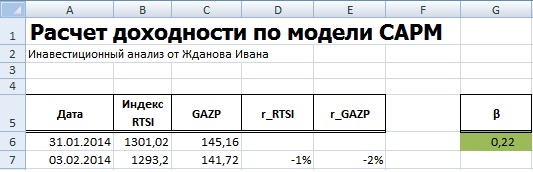
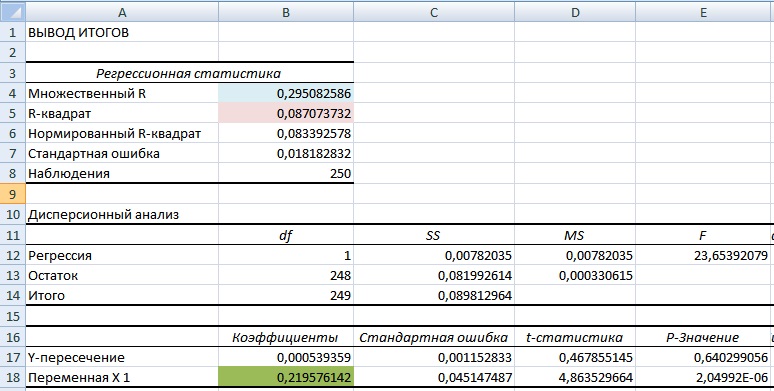
Расчет модели CAPM в ExcelДля того чтобы лучше понять модель CAPM разберем ее на реальном примере акций предприятия ОАО «Газпром». Для этого воспользуемся программой Excel. Получить котировки акций можно на сайте finam.ru в разделе «Про рынок» → «Экспорт данных». В нашей формуле за рыночную доходность будем брать изменения индекса РТС (RTSI), также это может быть индекс ММВБ (MICECX). Для американских акций зачастую берут изменения индекса S&P500. Были взяты ежедневные котировки акции и индекса за 1 год (250 данных), начиная с 31.01.2014 по 30.01.2015 г. Хочется заметить, что для оценки доходностей могла быть использована также формула расчета через натуральный логарифм: Итоговый результат расчета доходности одинаковый. На следующем этапе необходимо рассчитать значение коэффициента бета, отражающего рыночный риск акции. Для этого есть два варианта расчета. Расчет коэффициента бета с помощью формул ExcelДля расчета коэффициента бета можно воспользоваться формулой ИНДЕКС и ЛИНЕЙН, первая позволяет взять индекс b из формулы линейной регрессии между доходностями акции и индекса, который соответствует коэффициенту бета. Формула расчета будет следующая: Расчет коэффициента бета через надстройку «Регрессия»Второй вариант расчета рыночного риска модели заключается в использовании надстройки в разделе «Главное меню» → «Данные» →«Анализ данных» → «Регрессия». В открывшемся окне необходимо заполнить два поля: «Входной интервал Y» и «Входной интервал Х» доходностями индекса и акции соответственно. На новом листе Excel появится основные параметры модели линейной регрессии. В ячейке В18 отразится рассчитанный коэффициент линейной регрессии – коэффициент бета. Рассмотрим другие полученные параметры анализа. Так показатель Множественной R (коэффициента корреляции) между доходностью акции и индекса составляет 0,29, что показывает низкую степень зависимости доходности акции от доходности индекса. Коэффициент R-квадрат (коэффициент детерминированности) отражает точность полученной модели. Точность составляет 0,08, что очень мало для того чтобы принимать адекватные решения о прогнозировании будущей доходности на основе взаимосвязи только с уровнем риска рынка.
Что показывает коэффициент бета в модели CAPM?Коэффициент бета показывает чувствительность изменения доходности акции и доходности рынка. Другими словами, отражает рискованность вложения в тот или иной актив. Коэффициент бета служит мерой рыночного риска. Знак перед показателем отражает их однонаправленное или разнонаправленное движение. Рассмотрим более подробно значение бета в таблице ниже: Источник |