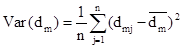Модель оценки доходности финансовых активов или

Модель оценки доходности финансовых активов

2. Модель оценки доходности финансовых активов.

С 1964 г. появляются новые работы, открывшие следующий этап в развитии инвестиционной теории, связанный с так называемой «моделью оценки капитальных активов» (или САРМ — от английского capital asset pricing model). Учеником Г. Марковица У. Шарпом была разработана модель рынка капиталов . Формулируя ее, он понимал, что абсолютно надежных акций или облигаций не бывает. Все они в той или иной степени связаны с риском для корпорации: она может получить большой доход или остаться без ничего. Развивая подход Г. Марковица, У. Шарп разделил теорию портфеля ценных бумаг на две части: первая — систематический (или рыночный) риск для активов акций, вторая — несистематический. Для обычной акции систематический риск всегда связан с изменениями в стоимости ценных бумаг, находящихся в обращении на рынке. Иначе говоря, доходность одной акции постоянно колеблется вокруг средней доходности всего актива ценных бумаг. Этого никак не избежать, поскольку действует слепой механизм рынка.

Несистематический риск связан с влиянием всех остальных факторов, специфических для корпорации, выпускающей в обращение ценные бумаги. Определив специальные коэффициенты реакции цен акций или облигаций на изменения рыночной конъюнктуры (знаменитые «альфу» и «бету» 3), У. Шарп разработал формулу расчета сравнительной меры риска ценных бумаг на основе «линии эффективности рынка заемного капитала».

Важным моментом систематического риска является то, что увеличение количества акций или облигаций не способно ликвидировать его. Однако растущая покупка ценных бумаг может повлечь за собой устранение несистематического риска. Отсюда получается, что вкладчик не может избежать риска, связанного с колебаниями конъюнктуры фондового рынка. Задача при формировании рыночного портфеля заключается в уменьшении риска путем приобретения различных ценных бумаг. И делается это так, чтобы факторы, специфические для отдельных корпораций, уравновешивали друг друга. Благодаря этому доходность портфеля приближается к средней для всего рынка.

На основе этой модели У. Шарп предложил упрощенный метод выбора оптимального портфеля, который сводил задачу квадратичной оптимизации к линейной. В более простых случаях (то есть для небольших размерностей) эта задача могла быть решена практически «вручную». Такое упрощение сделало методы портфельной оптимизации применимыми на практике. В 70-х годах ХХ в. развитие программирования, а также совершенствование статистической техники оценки коэффициентов «альфа» и «бета» отдельных ценных бумаг и индекса рынка в целом привели к появлению первых пакетов программ для решения задач управления портфелем ценных бумаг.

Разница между доходностью рыночного порт­феля и процентной ставкой называется премией за рыночный риск.

Выводы У. Шарпа стали известны как модели оценки долгосрочных активов, базирующиеся на предположении, что на конкурентном рынке ожидаемая премия за риск изменяется прямо пропорционально коэффициенту «бета».

Это означает, что если схематически представить инвестиции на рисунке, то все ин­вестиции должны располагаться вдоль наклонной линии, называемой лини­ей рынка ценных бумаг. Ожидаемая премия за риск инвестиций, бета которых равна 0,5, следовательно, составляет половину ожидаемой премии за рыноч­ный риск; ожидаемая премия за риск инвестиций с бетой, равной 2,0, в два раза превышает ожидаемую премию за рыночный риск. Мы можем предста­вить эту взаимосвязь в следующем виде:

Ожидаемая премия за риск акций =

= бета х ожидаемая премия за рыночный риск.

Инвестор всегда может получить ожидае­мую премию за риск b (r_т — r), комбинируя рыночный портфель и безриско­вые займы. Так, на хорошо функционирующем рынке никто не держит ак­ции, предлагающие премию за ожидаемый риск, меньше, чем b (r_т —r).

А как насчет других возможностей? Есть ли другие акции, которые обеспечивают более высокую ожидаемую премию за риск? Другими словами, существуют ли какие-либо акции, лежащие выше линии рынка ценных бумаг ? Если мы возьмем все акции в совокупности, мы получим рыночный пор­тфель. Следовательно, мы знаем, что акции в среднем располагаются на ли­нии. Так как ни одна не лежит ниже линии, то ни одна не может лежать и выше линии. Таким образом, каждая и любая акция должна лежать на линии рынка ценных бумаг и обеспечивать премию за ожидаемый риск, равную:

Рассмотрим четыре основных принципа выбора портфелей.

1. Инвесторы предпочитают высокую ожидаемую доходность инвестиций и низкое стандартное отклонение. Портфели обыкновенных акций, которые обеспечивают наиболее высокую ожидаемую доходность при данном стандартном отклонении, называются эффективными портфелями.

2. Если вы хотите знать предельное влияние акции на риск портфеля, вы должны учитывать не риск акции самой по себе, а ее вклад в риск пор­тфеля. Этот вклад зависит от чувствительности акции к изменениям стоимости портфеля.

3. Чувствительность акции к изменениям стоимости рыночного портфеля обозначается показателем бета. Следовательно, бета измеряет предель­ный вклад акции в риск рыночного портфеля.

4. Если инвесторы могут брать займы или предоставлять кредиты по без­рисковой ставке процента, тогда им следует всегда иметь комбинацию безрисковых инвестиций и портфель обыкновенных акций. Состав та­кого портфеля акций зависит только от того, как инвестор оценивает перспективы каждой акции, а не от его отношения к риску. Если инве­сторы не располагают какой-либо дополнительной информацией, им следует держать такой же портфель акций, как и у других,— иначе го­воря, им следует держать рыночный портфель ценных бумаг.

Далее, если каждый держит рыночный портфель и если бета показывает вклад каждой ценной бумаги в риск рыночного портфеля, тогда не удивительно, что премия за риск, требуемая инвесторами, пропорциональна коэффициенту бета.

Сегодня модель Г. Марковица используется в основном на первом этапе формирования портфеля активов при распределении инвестированного капитала по их различным типам (акциям, облигациям, недвижимости и т. п.). Однофакторная модель У. Шарпа используется на втором этапе, когда капитал, инвестированный в определенный сегмент рынка активов, распределяется между отдельными конкретными активами, составляющими выбранный сегмент (то есть по конкретным акциям, облигациям и т. п.).

В 60-х годах ХХ в. работы У. Шарпа, а затем также Дж. Линтнера и Я. Моссина были посвящены, по сути, одному вопросу: «Предположим, что все инвесторы, владея одной и той же информацией, одинаково оценивают доходность и риск отдельных акций. Предположим также, что все они формируют свои оптимальные, с точки зрения теории Г. Марковица, портфели акций, исходя из индивидуальной предрасположенности к риску. Как в этом случае сложатся цены на рынке акций?». Таким образом, на САРМ можно смотреть как на макроэкономическое обобщение теории Г. Марковица. Основным результатом САРМ стало установление соотношения между доходностью и риском активов для равновесного рынка. При этом важным оказывается тот факт, что при выборе оптимального портфеля инвестор должен учитывать не «весь» риск, связанный с активами (риск по Г. Марковицу), а только его часть, названную «систематическим», то есть «недиверсифицированным», риском. Эта часть риска активов тесно связана с общим риском рынка в целом и количественно представлена коэффициентом «бета», введенным У. Шарпом в его модели. Другая его часть (так называемый «несистематический», то есть «диверсифицированный», риск) ликвидируется выбором соответствующего (оптимального) портфеля. Связь между доходностью и риском носит линейный характер, и тем самым привычное практическое правило «большая доходность означает большой риск» получает точное аналитическое обоснование.

В 1977 г. эта теория была подвергнута жесткой критике в работах Р. Ролла. Он высказал мнение, что САРМ нужно отбросить, поскольку ее в принципе нельзя эмпирически проверить. Несмотря на это, САРМ остается, вероятно, наиболее значительной и наиболее влиятельной современной финансовой теорией. Более того: на ее основе была разработана формула ценообразования на опционы, названная в честь американских ученых Ф. Блэка и М. Скоулза — первых, кто ее вывел.

Прежде чем выяснить суть этой формулы, кратко остановимся на экономической роли производных ценных бумаг — в частности, одной их разновидности — опциона. В отличие от акций и облигаций, выпускаемых с целью привлечения денежных средств, опционы покупают и продают фирмы, чтобы защититься от неблагоприятных изменений на финансовом рынке. Именно потому, что стоимость опционов является производной от стоимости других ценных бумаг, их называют «вторичными». Существование рынка вторичных ценных бумаг позволяет его участникам, ожидающим в будущем каких-то поступлений (или, наоборот, затрат), гарантировать себе определенный уровень прибыли или застраховаться от потерь, превышающих определенный уровень. В последние 20 лет такой рынок стремительно развивается во всем мире .

Любое вложение в опцион является более рисковым, чем вложение непосредственно в акции: ведь риск, связанный с ним, изменяется каждый раз, когда изменяется цена акции. Соответственно, ожидаемая норма дохода на опцион, на которую рассчитывают инвесторы, ежечасно изменяется в зависимости от изменения рыночной цены акции. Именно поэтому определение стоимости опционов при помощи стандартных формул казалось практически невозможным, а разработка техники точной оценки этой стоимости на протяжении многих лет была не по силам экономистам. Все предыдущие (с 1900 г.) попытки определить стоимость вторичных ценных бумаг были неудачными из-за огромной проблемы — невозможности правильно исчислить премию за риск (доход на рисковые вложения).

М. Скоулз и Ф. Блэк совершили прорыв в этой области, разработав метод определения стоимости опциона, не требующий использования конкретной величины премии за риск. Однако это не означает, что премии за риск нет: просто она включена в цену акции. Именно эту идею оба ученых впервые обосновали в работе «Ценообразование на опционы и пассивы корпораций» (1973 г.). В этот период они тесно сотрудничали с Р. Мертоном, который также занимался проблемой оценки опционов. Он внес ряд предложений, которые улучшали упомянутую статью. В частности, соглашаясь с предположением относительно непрерывности осуществления операций с опционами и акциями, Р. Мертон предложил поддерживать между ними такое соотношение, которое является полностью безрисковым. Он придумал важное обобщение, согласно которому рыночное равновесие не является обязательным условием для оценки опциона, будучи для нее достаточным условием, если нет возможностей осуществить арбитражные операции. Опубликованная им статья «Теория рационального ценообразования опционов» (1973 г.) тоже включала формулу Блэка — Скоулза и некоторые обобщения (например, он предположил стохастичность процентной ставки).

Таким образом, эта формула оценивает «справедливую стоимость» опциона. Она полезна при принятии инвестиционных решений, но не гарантирует прибыли на опционных торгах. Концептуально формулу Блэка — Скоулза можно объяснить так: цена опциона «колл» = (ожидаемая цена акции) — (ожидаемая стоимость выполнения опциона). Она имеет такой математический вид:

C = SN(d) — Le -rt N(d -√t)

где С — теоретическая оценка опциона «колл» (которую также называют «премией»), S — текущая цена акции, N — количество акций, L — страйк опциона, t — время до экспирации (конца действия) опциона (в годах), q — среднее квадратичное отклонение курса акции (корень из суммы квадратов отклонений), r — безрисковая процентная ставка, е — основа натурального логарифма (2,71828), где d — дивидендная доходность акции, ln — натуральный логарифм.

Эта формула основывалась на возможности осуществления безрисковой сделки с одновременным использованием акции и выписанным на нее опционом. Стоимость (цена) такой сделки должна совпадать со стоимостью безрисковых активов на рынке, а поскольку цена акции со временем изменяется, то и стоимость выписанного опциона, обеспечивающего безрисковую сделку, тоже должна соответственно изменяться. Из этих предписаний можно получить вероятностную оценку стоимости опциона.

Источник

Модель оценки доходности финансовых активов

Любая организация может рассматриваться как совокупность некоторых активов, находящихся в определенном сочетании. Владение любым из этих активов связано с определенным риском в плане воздействия на этого актива на величину общего дохода организации.

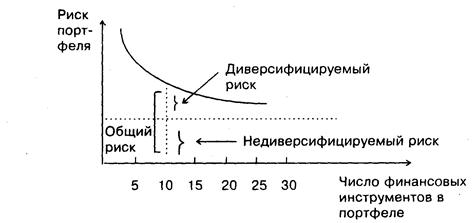
Это утверждение вполне уместно и для портфеля ценных бумаг, которыми обладает коммерческий банк. Очевидно, что степень риска изменяется обратно пропорционально количеству включенных в портфель случайным образом видов ценных бумаг (Рисунок 6.1). А общий риск портфеля состоит из двух частей:

· диверсифицируемый (несистематический) риск, т.е. риск, который может быть элиминирован за счет диверсификации (инвестиро­вание 1 млн. руб. в акции десяти компаний менее рискованно, нежели инвестирование той же суммы в акции одной компании);

· недиверсифицируемый (систематический, или рыночный) риск, т.е. риск, который нельзя уменьшить путем изменения структуры портфеля.

Рис. 6.1. Зависимость степени риска от диверсификации портфеля

Исследования показали, что если портфель состоит из 10–20 различных видов ценных бумаг, включенных в портфель с помощью случайной выборки из имеющегося на рынке ценных бумаг набора, то несистематический риск может быть сведен к минимуму (это по­казано и на рис. 1). Таким образом, этот риск поддается элимини­рованию довольно несложными методами, поэтому основное вни­мание следует уделять возможному уменьшению систематического риска.

В экономической теории существует «теория портфеля» (portfolio theory) – теория финансовых инвестиций, в рамках которой с помо­щью статистических методов и осуществляются наиболее выгодное распределение риска портфеля ценных бумаг и оценка прибыли. Эта теория состоит из четырех основных элементов:

· оценка активов (security valuation);

· инвестиционные решения (asset allocation decision);

· оптимизация портфеля (portfolio optimization);

· оценка результатов (performance measurement).

В процессе управления инвестиционным портфелем менеджер постоянно сталкивается с задачей отбора новых инструментов и ана­лиза возможности их включения в портфель. Какими же методами можно это делать? Существует несколько способов, однако наибольшую известность получила модель оценки доходности финансовых активов (Capital Asset Pricing Model, САРМ), увязывающая систематический риск и доходность портфеля.

Как и любая теория финансов, модель CAPM сопровождается рядом предпосылок, которые в акцентированном виде были сформули­рованы М. Дженсеном и опубликованы им в 1972 г. [Jensen, 1972]. Эти предпосылки таковы.

1.Основной целью каждого инвестора является максимизация возможного прироста своего богатства на конец планируемого периода путем оценки ожидаемых доходностей и среднеквадратических отклонений альтернативных инвестиционных портфелей.

2.Все инвесторы могут брать и давать ссуды неограниченного размера по некоторой безрисковой процентной ставке d_rf, при этом не существует ограничений на «короткие» продажи любых активов[1].

3.Все инвесторы одинаково оценивают величину ожидаемых зна­чений доходности, дисперсии и ковариации всех активов; это означа­ет, что инвесторы находятся в равных условиях в отношении прогно­зирования показателей.

4.Все активы абсолютно делимы и совершенно ликвидны (т.е. всегда могут быть проданы на рынке по существующей цене).

5.Не существует трансакционных расходов.

6.Не принимаются во внимание налоги.

7.Все инвесторы принимают цену как экзогенно заданную ве­личину (т.е. они полагают, что их деятельность по покупке и про­даже ценных бумаг не оказывает влияния на уровень цен на рынке этих бумаг).

8.Количество всех финансовых активов заранее определено и фиксировано.

Как легко заметить, многие из сформулированных предпосылок носят исключительно теоретический характер и не могут быть выпол­нены на практике.

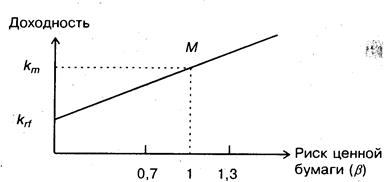
Для понимания логики модели легче всего воспользоваться гра­фическим представлением (Рисунок 6.2). Ставится задача найти взаимо­связь между ожидаемой доходностью (у) и риском ценной бумаги (х), т.е. построить функцию у = f(x). Построение основывается на следующих очевидных рассуждениях:

· доходность ценной бумаги связана с присущим ей риском прямой связью;

· риск характеризу­ется некоторым показателем b;

· «средней» ценной бумаге, т.е. бу­маге, имеющей средние значения риска и доходности, соответствуют b=1 и доходность d_m;

· имеются безрисковые ценные бумаги со ставкой d_rf и b = 0.

Исходя из приведенных выше предпосылок доказывается, что ис­комая зависимость у = f(x) представляет собой прямую линию. Итак, мы имеем две точки с координатами (0, d_rf) и (1, d_m). Из курса геометрии известно, что уравнение прямой, проходящей через точки (х₁, у₁) и (х₂, у₂), задается формулой

(6.8)

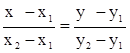
Подставляя в формулу исходные данные, получим:

(6.9)

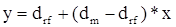
Рисунок 6.2. Логика представления модели CAPM

Имея в виду, что переменная х представляет собой риск, харак­теризуемый показателем b, а у – ожидаемую доходность d_ex, полу­чим следующую формулу, которая и представляет собой модель САРМ:

(6.10)

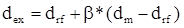
где d_ex – ожидаемая доходность акций данной компании;

d_rf – доходность безрисковых ценных бумаг (в частности, в США берут за осно­ву государственные казначейские векселя, используемые для краткосрочного (до 1 года) регулирования денежного рынка);

d_m – ожидаемая доходность в среднем на рынке ценных бумаг;

b – бета-коэффициент данной компании.

Показатель (d_m – d_rf) имеет вполне наглядную интерпретацию, представляя собой рыночную (т.е. в среднем) премию за риск вло­жения своего капитала не в безрисковые государственные ценные бумаги, а в рисковые ценные бумаги (акции, облигации корпорации и пр.). Аналогично показатель (d_ex – d_rf) представляет собой премию за риск вложения капитала в ценные бумаги именно данной компа­нии. Модель САРМ означает, что премия за риск вложения в ценные бумаги данной компании прямо пропорциональна рыночной премии за риск.

Модель САРМ позволяет прогнозировать доходность финансово­го актива. В свою очередь, зная этот показатель и имея данные об ожи­даемых доходах по этому активу, можно рассчитать его теоретическую стоимость. Не случайно поэтому модель САРМ называют еще моде­лью ценообразования финансовых активов.

Систематический риск в рамках модели САРМ измеряется с помощью b-коэффициентов (бета-коэффициентов). Каждый вид ценной бумаги имеет собственный b-коэффициент, представляющий собой индекс доходности данного актива по отношению к доходности в среднем на рынке ценных бумаг. Значение показателя b рассчитывается по статистическим данным для каждой компании, котирующей свои ценные бумаги на бирже, и периодически публикуется в специ­альных справочниках. Для каждой компании b меняется с течением времени и зависит от многих факторов, в частности имеющих отношение к характеристике деятельности компании с позиции долгосроч­ной перспективы. Очевидно, что сюда относится, прежде всего, пока­затель уровня финансового левериджа, отражающего структуру ис­точников средств: при прочих равных условиях, чем выше доля заемного капитала, тем более рисковая компания и тем выше ее b[2].

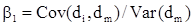
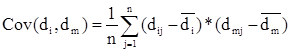
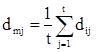
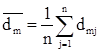
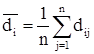
Например, имеется совокупность показателей доходности по груп­пе компаний за ряд периодов ij>, где: d_ij – показатель доходности i-й компании (i = 1,2. ,t) j-м периоде (j = 1,2. n). Тогда формула расчета b-коэффициента для любой i-й компании имеет вид:

(6.11)

где ;

– доходность в среднем на рынке ценных бумаг j-м периоде;

– доходность в среднем на рынке ценных бумаг за все периоды;

– доходность ценных бумаг i-й компании в среднем за все периоды.

В целом по рынку ценных бумаг b-коэффициент равен единице; для отдельных компаний он колеблется около единицы, причем большинство b-коэффициентов находится в интервале от 0,5 до 2,0. Интерпретация b-коэффициента для акций конкретной компании заключается в следующем:

· b = 1 означает, что акции данной компании имеют среднюю степень риска, сложившуюся на рынке в целом;

· b 1 означает, что ценные бумаги данной компании более рискованны, чем в среднем на рынке;

· увеличение b-коэффициента в динамике означает, что вложения в ценные бумаги данной компании становятся более рискованными;

· снижение b-коэффициента в динамике означает, что вложения в ценные бумаги данной компании становятся менее рискованными.

В качестве примера можно привести усредненные данные о b-коэффициентах ряда американских компаний в 1987–1991 гг.:

· наивысшие значения b-коэффициентов имели компании:

American Express – 1,5;

Bank America – 1,4;

· средние значения b-коэффициентов имели компании:

Digital Equipment – 1,1;

Walt Disney – 0,9;

· наименьшие значения b-коэффициентов имели компании:

General Mills – 0,5;

Southern California Edison – 0,5.

Следует отметить, что единого подхода к исчислению b-коэффи-циентов, в частности в отношении количества и вида исходных наблюдений, не существует. Так, известный американский банкирский дом «Merrill Lynch», занимающийся также и публикацией различных рыночных индикаторов, при расчете b-коэффициентов компаний в качестве d_m использует индекс S&P 500 и месячные данные о доход­ности компаний за пять лет, т.е. 60 наблюдений. Другая компания «Value Line», занимающаяся подобной деятельностью, ориентирует­ся на индекс курсов акций Нью-йоркской фондовой биржи (NYSE Composite Index), включающий данные о доходности обыкновенных акций более чем 1800 компаний, и использует 260 недельных на­блюдений.

С 1995 г. b-коэффициенты появились и на отечественном рынке ценных бумаг. Расчеты выполняются информационно-аналитическим агентством «Анализ, консультация и маркетинг» (АК&М), однако спи­сок компаний, как правило, не превышает полутора десятков, охваты­вая в основном предприятия энергетики и нефтегазового комплекса. Значения b-коэффициентов достаточно ощутимо варьируют. Так, в ян­варе 1997 г. нефтедобывающая отрасль имела b = 0,9313, а нефтехими­ческая – b = 0,1844. b-коэффициенты периодически публикуются в газете «Финансовые известия».

Пример: Расчет ожидаемой доходности финансового актива

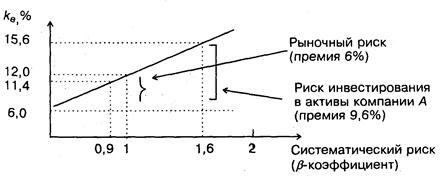
Рассматривается целесообразность инвестирования в акции ком­пании А, имеющей b=1,6 или компании Б, имеющей b=0.9, если d_rf = 6%; d_m = 12%. Инвестиция делается в том случае, если доход­ность составляет не менее 15%.

Необходимые для принятия решения оценки можно рассчитать с помощью модели САРМ. По формуле (10) находим:

для компании А: d_ex = 6% + 1.6 * (12% – 6%) = 15.6%,

для компании Б: d_ex = 6% + 0.9 * (12% – 6%) = 11.4%.

Таким образом, наиболее целесообразной является инвестиция в акции компании А.

Для наглядности логика взаимосвязи рассмотренных показателей может быть объяснена с помощью графика, носящего название линии рынка ценных бумаг (Security Market Line, SML). График SML отражает линейную зависимость «доходность/риск» для конкретных ценных бумаг и выглядит следующим образом (Рисунок 6.3).

Важным свойством модели САРМ является ее линейность отно­сительно степени риска. Это дает возможность определять b-коэффициент портфеля как средневзвешенную b-коэффициентов входящих в портфель финансовых активов.

(6.12)

b_i – значение бета-коэффициента i-го актива в портфеле;

b_p – значение бета-коэффициента портфеля;

d_i – доля i-го актива в портфеле;

n – число различных финансовых активов в портфеле.

Рис. 6.3. График линии рынка ценных бумаг

Пример: Расчет b-коэффициента портфеля ценных бумаг

Портфель включает следующие активы:

• 12% акции компании А, имеющие b = 1;

• 18% акции компании В, имеющие b = 1,2;

• 25% акции компании С, имеющие b = 1,8;

• 45% акции компании D, имеющие b = 0,7.

Тогда b-коэффициент инвестиционного портфеля будет равен:

Обобщением понятия «линия рынка ценных бумаг» является линия рынка капитала (Capital Market Line, CML), отражающая зависимость (доходность/риск) для эффективных портфелей, которые, как правило, сочетают безрисковые и рисковые активы.

Линию рынка капитала можно использовать для сравнительного анализа портфельных инвестиций. Как следует из модели САРМ, каж­дому портфелю соответствует точка в квадранте на рис. 2. Возмож­ны три варианта расположения этой точки: на линии рынка капитала, ниже или выше этой линии. В первом случае портфель называется эффективным, во втором – неэффективным, в третьем – сверхэф­фективным.

Как отмечено выше, модель САРМ разработана исходя из ряда пред­посылок, часть из которых не выполняется на практике, например, налоги и трансакционные затраты существуют, инвесторы находятся в неравных условиях, в том числе и в отношении доступности инфор­мации и т.п. Поэтому модель не является идеальной и неоднократно подвергалась как критике, так и эмпирической проверке. Существуют различные точки зрения по поводу модели, поэтому приведем неко­торые наиболее типовые представления о современном состоянии этой теории из обзора, сделанного Ю.Бригхемом и Л.Гапенски:

· концепция САРМ, в основе которой лежит приоритет рыночного риска перед общим, является весьма полезной, имеющей фундаментальное значение в концептуальном плане. Модель логично отражает поведение инвестора, стремящегося максимизировать свой доход при заданном уровне риска и доступности данных;

· теоретически CAPM дает однозначное и хорошо интерпретируемое представление о взаимосвязи между риском и требуемой доход­ностью, однако она предполагает, что для построения связи должны использоваться априорные ожидаемые значения переменных, тогда как в распоряжении аналитика имеются лишь апостериорные факти­ческие значения. Поэтому оценки доходности, найденные с помощью модели, потенциально содержат ошибки;

· некоторые исследования, посвященные эмпирической провер­ке модели, показали на значительные отклонения между фактичес­кими и расчетными данными, что позволило ряду ученых подверг­нуть эту теорию серьезной критике. В частности, к ним относятся Ю. Фама и К. Френч, которые изучили зависимость между b-коэффциентами и доходностью нескольких тысяч акций по данным за пятьдесят лет. По мнению Бригхема и Гапенски, модель САРМ описывает взаимосвязи между ожидаемыми значениями перемен­ных, поэтому любые выводы, основанные на эмпирической провер­ке статистических данных, вряд ли правомочны и не могут опровер­гнуть теорию.

Тем не менее многие ученые понимают, что один из основных не­достатков модели заключается в том, что она является однофактор­ной. Указывая на этот недостаток, известные специалисты Дж. Уэстон и Т. Коуплэнд приводят такой образный пример. Представьте себе, что ваш маленький самолет не может совершить посадку из-за силь­ного тумана, и на вопрос диспетчерам о помощи вы получите инфор­мацию о том, что самолет находится в ста милях от посадочной поло­сы. Конечно, информация весьма полезна, но вряд ли достаточна для успешной посадки.

В научной литературе известны три основных подхода, альтерна­тивные модели САРМ: теория арбитражного ценообразования, тео­рия ценообразования опционов и теория преференций состояний в условиях неопределенности.

Наибольшую известность получила теория арбитражного ценообразования (Arbitrage Pricing Theory, APT). Концепция APT была предложена известным специалистом в области финансов, профессором Йельского университета Стивеном Россом. В основу модели за­ложено естественное утверждение о том, что фактическая доходность любой акции складывается из двух частей: нормальной, или ожидае­мой, доходности и рисковой, или неопределенной, доходности. Пос­ледний компонент определяется многими экономическими фактора­ми, например рыночной ситуацией в стране, оцениваемой валовым внутренним продуктом, стабильностью мировой экономики, инфля­цией, динамикой процентных ставок и др. Таким образом, модель может и должна включать множество факторов и в наиболее общем виде описывается следующей зависимостью:

(6.13)

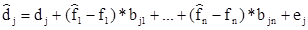
где d_j – фактическая доходность j-й ценной бумаги;

d_j – ожидаемая доходность j-й ценной бумаги;

f_i – фактическое значение i-го экономического фактора;

f_i – ожидаемое значение i-го экономического фактора;

b_ji – чувствительность j-й ценной бумаги к i-му экономическому фактору;

e_j – влияние не включенных в модель специфических факторов на изменение доходности j-й ценной бумаги.

Данная модель обладает как достоинствами, так и недостатками. Прежде всего она не предусматривает таких жестких исходных предпосылок, которые свойственны модели САРМ. Количество и состав релевантных факторов определяются аналитиком и заранее не регламентируются. Фактическая реализация модели связана с привлечением достаточно сложного аппарата математической статистики, поэтому до настоящего времени теория APT носит достаточно теоретический характер. Тем не менее, главное достоинство этой теории, заключающееся в том, что доходность является функцией многих переменных, весьма привлекательна, и потому эта теория рассматрива­ется многими учеными как одна из наиболее перспективных.

Две другие альтернативы модели САРМ – теория ценообразова­ния опционов (Option Pricing Theory, OPT) и теория преференций со­стояний в условиях неопределенности (State-Preference Theory, SPT), – по тем или иным причинам еще не получили достаточного развития и находятся в стадии становления. По этой причине мы опускаем их рассмотрение в нашем курсе.

Источник