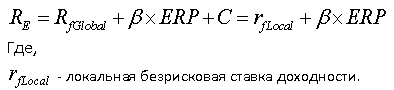Модель оценки доходности финансовых активов (САРМ)
Модель оценки доходности финансовых активов (Capital Asset Pricing Model, САРМ), увязывающая систематический риск и доходность актива. Как и любая теория финансов, модель САРМ сопровождается рядом предпосылок, которые в акцентированном виде были сформулированы М.
1. Основной целью каждого инвестора является максимизация возможного прироста своего богатства на конец планируемого периода путем оценки ожидаемых доходностей и среднеквадратических отклонений альтернативных инвестиционных портфелей.
2. Все инвесторы могут брать и давать ссуды неограниченного размера по некоторой безрисковой процентной ставке Cf при этом не существует ограничений на «короткие» продажи любых активов.
3. Все инвесторы одинаково оценивают величин>’ ожидаемых значений доходности, дисперсии и ковариации всех активов; это означает, что инвесторы находятся в равных условиях в отношении прогнозирования показателей.
4. Все активы абсолютно делимы и совершенно ликвидны (т. е. всегда могут быть проданы на рынке по существующей цене).
5. Не существует трансакционных расходов.
6. Не принимаются во внимание налоги.
7. Все инвесторы принимают цену как экзогенно заданную величину (т. е. они полагают, что их деятельность по покупке и продаже ценных бумаг не оказывает влияния на уровень цен на рынке этих бумаг).
8. Количество всех финансовых активов заранее определено и фиксировано.
Как легко заметить, многие из сформулированных предпосылок носят исключительно теоретический характер и не могут быть выполнены на практике.
Модель оценки доходности финансовых активов (САРМ) предполагает, что цена собственного капитала Ce
пявня безпискоиой ттохоттности плюс ттпемия зя систематический ПИСК·
 |
где Cf- доходность безрисковых вложений;
P — коэффициент, рассчитываемый для каждой акции;
Cm — средняя ставка доходности, сложившаяся на рынке ценных бумаг.
Основа вычисления стоимости капитала по САРМ — безрисковая доходность, Cf. В качестве безрисковой ставки дохода в мировой практике используют обычно ставку дохода по долгосрочным государственным долговым обязательствам (облигациям или векселям); считают, что государство — самый надежный гарант по своим обязательствам (вероятность его банкротства практически исключаема). Однако, как показывает практика, государственные ценные бумаги в России не воспринимают как безрисковые. Для определения ставки дисконта в качестве безрисковой может быть принята ставка по вложениям, характеризующимся наименьшим уровнем риска (ставка по валютным депозитам в Сбербанке или других наиболее надежных банках). Можно также основываться на безрисковой ставке для западных компаний, но в этом случае обязательно прибавление странового риска с целью учета реальных условий инвестирования, существующих в России. Для инвестора она представляет собой альтернативную ставку дохода, которую характеризуют практическим отсутствием риска и высокой степенью ликвидности. Безрисковую ставку используют как точку отсчета для оценки различных видов риска, характеризующих вложения в данное предприятие, на основе чего и выстраивают требуемую ставку дохода.
Таким образом, показатель (Cm — Cf) — имеет вполне наглядную интерпретацию, представляя собой рыночную (т.е. в среднем) премию за риск вложения своего капитала не в безрисковые государственные ценные бумаги, а в рисковые ценные бумаги (акции, облигации корпораций и пр.). Аналогично показатель (Се — Cf) представляет собой премию за риск вложения капитала в ценные бумаги именно данной компании. Модель САРМ означает, что премия за риск вложения в ценные бумаги данной компании прямо пропорциональна рыночной премии за риск.
Модель позволяет спрогнозировать доходность финансового актива; в свою очередь, зная этот показатель и имея данные об ожидаемых доходах по этому активу, можно рассчитать его теоретическую стоимость. Не случайно поэтому модель называют еще моделью ценообразования финансовых активов.
Систематический риск в рамках модели САРМ измеряется с помощью β-коэффициентов (бета-коэффициентов). Каждый вид ценной бумаги имеет собственный β-коэффициент, представляющий собой индекс доходности данного актива по отношению к доходности в среднем на рынке ценных бумаг. Значение показателя β рассчитывается по статистическим данным для каждой компании, котирующей свои ценные бумаги на бирже, и периодически публикуется в специальных справочниках. Для каждой компании β меняется с течением времени и зависит от многих факторов, в частности имеющих отношение к характеристике деятельности компании с позиции долгосрочной перспективы. Очевидно, что сюда относится, прежде всего, показатель уровня финансового левериджа, отражающего структуру источников средств: при прочих равных условиях чем выше доля заемного капитала, тем более рисковая компания и тем выше ее β.
В целом по рынку Ценных бумаг β-коэффициент равен единице; для отдельных компаний он колеблется около единицы, причем большинство β-коэффициентов находится в интервале от 0,5 до 2,0. Интерпретация β-коэффициента для акций конкретной компании заключается в следующем31:
• β = 1 означает, что акция данной компании имеют среднюю степень риска, сложившуюся на рынке в целом;
• β 1 означает, что ценные бумаги данной компании более рискованны, чем в среднем на рынке;
• увеличение β-коэффициента в динамике означает, что вложения в ценные бумаги данной компании становятся более рискованными;
• снижение β-коэффициента в динамике означает, что вложения ценные бумаги данной компании становятся менее рискованными.
Пример 3.1. Рассматривается целесообразность инвестирования в акции компании А, имеющей бета- коэффициент равный 1,6, или компании В, имеющей коэффициент бета равный 0,9.
Необходимые для принятия решения оценки можно рассчитать с помощью модели САРМ.
Для компании A: Ce = 6 + 1,6*(12-6) = 15,6 %
Для компании В: Ce = 6 + 0,9 *(12-6) =11,4%
Таким образом, инвестиции в акции компании А более целесообразно.
Важным свойством модели САРМ является ее линейность относительно степени риска. Это дает возможность определять β-коэффициент портфеля как средневзвешенную β-коэффициентов входящих в портфель активов.
Пример 3.2. Найти коэффициент бета портфеля активов. Портфель включает следующие активы: А — 14%>; В — 28%; C — 35%; D -13%; E-10%. Коэффициент бета составляет А — 1,3; В — 1,6; C — 0,7; D — 0,9; E — 1.
Решение βρ = 0,14 * 1,3 + 0,28 * 1,6 + 0,35 * 0,7 + 0,13 * 0,9 + 0,1 * 1 = 1,092
Как отмечено выше, модель САРМ разработана исходя из ряда предпосылок, часть из которых не выполняется на практике, например, налоги и трансакционные затраты существуют, инвесторы находятся в неравных условиях, в том числе и в отношении доступности информации и т.п. Поэтому модель не является идеальной и неоднократно подвергалась как критике, так и эмпирической проверке. Особенно интенсивно исследования в этом направлении велись с конца 60-х годов, а их результаты нашли отражение в сотнях статей. Существуют различные точки зрения по поводу модели, поэтому приведем некоторые наиболее типовые представления о современном состоянии этой теории из обзора, сделанного Ю.Бригхемом и Л.Гапенски.
1. Концепция САРМ, в основе которой лежит приоритет рыночного риска перед общим, является весьма полезной, имеющей фундаментальное значение в концептуальном плане. Модель логично отражает поведение инвестора, стремящегося максимизировать свой доход при заданном уровне риска и доступности данных.
2. Теоретически САРМ однозначное и хорошо интерпретируемое представление о взаимосвязи между риском и требуемой доходностью, однако она предполагает, что для построения связи должны использоваться априорные (ожидаемые) значения переменных, тогда как в распоряжении аналитика имеются лишь апостериорные (фактические) значения.
3. Некоторые исследования, посвященные эмпирической проверке модели, показали на значительные отклонения между фактическими и расчетными данными, что позволило ряду ученых подвергнуть эту теорию серьезной критике. В частности, к ним относятся Ю.Фама и К.Френч, которые изучили зависимость между β- коэффициентами и доходностью нескольких тысяч акций по данным за пятьдесят лет. По мнению Бригхема и Гапенски, модель САРМ описывает взаимосвязи между ожидаемыми значениями переменных, поэтому любые выводы, основанные на эмпирической проверке статистических данных, вряд ли правомочны и не могут опровергнуть теорию,
Тем не менее, многие ученые понимают, что один из основных недостатков модели заключается в том, что она является однофакторной. Указывая на этот недостаток, известные специалисты Дж. Уэстон и Т. Коуплэнд приводят такой образный пример. Представьте себе, что ваш маленький самолет не может совершить посадку из-за сильного тумана, и на вопрос диспетчерам о помощи вы получите информацию о том, что самолет находится в ста милях от посадочной полосы. Конечно, информация весьма полезна, но вряд ли достаточна для успешной посадки.
В научной литературе известны три основных подхода, альтернативные модели САРМ: теория арбитражного ценообразования, теория ценообразования опционов и теория преференций состояний в условиях неопределенности.
3.2 Теория арбитражного ценообразования (APT)
Наибольшую известность получила теория арбитражного ценообразования (Arbitrage Pricing Theory, APT). Концепция APT была предложена известным специалистом в области финансов, профессором Йельского университета Стивеном Россом. В основу модели заложено естественное утверждение о том, что фактическая доходность любой акции складывается из двух частей: нормальной, или ожидаемой, доходности и рисковой, или неопределенной, доходности. Последний компонент определяется многими экономическими факторами, например рыночной ситуацией в стране, оцениваемой валовым внутренним продуктом, стабильностью мировой экономики,
инфляцией, динамикой процентных ставок и др.
Ce = Cf + C1 +C2 +. + Cn, (3.2)
где Cf- доходность безрисковых вложений;
Cl, C2, Cn- премии за различного рода риски.
 |
Данная модель обладает как достоинствами, так и недостатками. Прежде всего она не предусматривает таких жестких исходных предпосылок, которые свойственны модели САРМ. Количество и состав релевантных факторов определяются аналитиком и заранее не регламентируются. Фактическая реализация модели связана с привлечением достаточно сложного аппарата математической статистики, поэтому до настоящего времени теория APT носит достаточно теоретизированный характер. Тем не менее, главное достоинство этой теории, заключающееся в том, что доходность является функцией многих переменных, весьма привлекательна, и потому эта теория рассматривается многими учеными как одна из наиболее перспективных.32
C помощью модели Гордона определить стоимость собственного капитала можно следующим образом:
| class=»lazyload» data-src=»https://scicenter.online/files/uch_group44/uch_pgroup319/uch_uch1150/image/33.jpg»> |
где Ce — стоимость собственного капитала, привлекаемого за счет эмиссии обыкновенных акций; Dl- прогнозное значение дивиденда на ближайший период;
Po — текущая (рыночная) цена обыкновенной акции; g — прогнозируемый темп прироста дивидендов.
В практике наиболее сложно оценить ставку прироста g. Эго можно сделать несколькими способами:
• использовать ранее установленные ставки;
• использовать метод экспертных оценок;
• рассчитать среднеарифметический прирост за предыдущие годы выплат дивидендов.
Пример 3.2. Дивиденды предприятия в прошлом году составили 10%. Его ценные бумаги в настоящий момент продают по цене 3000 руб. за акцию. Вы рассчитываете, что в будущем дивиденды будут стабильно возрастать на 10%. Какова стоимость активов предприятия? Прибыль на следующий год Dl составит:
Do = Номинал акции *ставка дивидендов = 3000*0,1 =300 руб.
Dl = Do* (I + g) = 300*(1 + 0,1) = 330руб.
 |
Следовательно, стоимость активов Ce составит:
Однако алгоритм расчетов методом Гордона имеет некоторые недостатки. Во-первых, он может быть реализован лишь для предприятий, выплачивающих дивиденды. Во-вторых, показатель Ce очень чувствителен к изменению коэффициента g (так, при данной стоимости ценной бумаги завышение значения g всего на 0,1% повлечет за собой завышение оценки стоимости капитала по меньшей мере на 1%). В-третьих, здесь не учтен рыночный риск. Эти недостатки в известной степени устраняются при применении модели САРМ.
Вопросы для самоконтроля
1. Объясните смысл модели САРМ.
2. Объясните важность и значение β-коэффициента.
3. Назовите основные достоинства и недостатки модели САРМ.
4. Объясните смысл модели APT. Кто является автором данной модели?
5. Назовите основные достоинства и недостатки модели APT.
6. Объясните смысл модели Гордона. Назовите основные недостатки и достоинства модели.
7. Для чего применяются основные модели оценки активов?
Источник
САРМ. Модель ценообразования активов (Capital Asset Pricing Model)
Распространенным подходом к оценке уровня премий за акционерный риск, применяемым на практике основными инвестбанками и аудиторами, является модель САРМ (Capital Asset Pricing Model), другое название – модель ценообразования на рынке капитальных финансовых активов, изредка в учебной литературе встречается аббревиатура МОДА, то есть «модель оценки долгосрочных активов».
Модель CAPM, чаще всего, применяется для объяснения динамики курсов ценных бумаг и функционирования механизма, посредством которого инвесторы могли бы оценивать влияние инвестиций в предполагаемые ценные бумаги на риск и доходность их портфеля.
Концепция этой модели была разработана в 1950-х гг. в США Гарри Марковицем [1], дальнейшее развитие модель получила в работах Jack Treynor (1961-1962гг.), William Sharpe (1964г.), John Lintner (1965г.) и Jan Mossin (1966г.).
Суть САРМ модели заключается в следующем: предполагая существование высоколиквидного эффективного рынка финансовых активов, можно прийти к выводу о том, что величина требуемой отдачи на средства, вложенные в какой-либо актив, определяется не столько специфическим риском, присущим конкретному активу, сколько общим уровнем риска, характерным для фондового рынка.[2]
Такой вывод может показаться противоречащим здравому смыслу – инвестору должен быть компенсирован тот риск, который он принимает, вкладывая ресурсы в капитал компании. Логика модели базируется на том, что инвестор диверсифицирует свои вложения и, хотя для разных вложений, входящих в портфель активов инвестора, характерен разный профиль риска, зачастую потери от одного актива могут быть компенсированы доходами по другому активу, что существенным образом снижает реальный уровень риска, принимаемого на себя инвестором.
Математически формула определения ожидаемой ставки доходности на долгосрочный актив имеет следующий вид:
где,
Rf — доходность безрисковых активов, под которой, как правило, понимают доходность государственных ценных бумаг;
Rm — ожидаемая средняя норма прибыли рыночного портфеля;
(Rm-Rf) — премия за риск вложения в акции (в ряде учебных пособий премия за рыночный риск принимается равной 5%);
β — коэффициент, характеризующий чувствительность оцениваемой ценной бумаги к изменениям рыночной доходности (рассчитывается по статистическим данным и выражает вариабельность доходности ценной бумаги по отношению к среднерыночной доходности).
Смысл модели CAPM заключается в том, что требуемая (рыночная) доходность собственного капитала есть безрисковая ставка доходности, увеличенная на риски, соответствующие акционерному капиталу.
Применительно к российской практике можно говорить о двух подходах для расчета по модели CAPM для компаний из развивающихся рынков.
Подходы к расчету модели CAPM:
Страновой риск корректируется на β-коэффициент
Страновой риск не корректируется на β-коэффициент
Если страновой риск корректируется на β-коэффициент, формула для CAPM принимает следующий вид:
В случае, когда страновой риск не корректируется на β-коэффициент, формула для CAPM принимает следующий вид:
Для непубличных компаний вышеприведенные формулы CAPM для расчета ставки дисконтирования могут дополняться показателями S1 и S2 — премиями за малый размер и специфические риски соответственно.
где,
S1 — дополнительная норма дохода за риск инвестирования в конкретную компанию;
S2 — дополнительная норма дохода за риск инвестирования в малую компанию.
Говоря о безрисковой ставке, следует пояснить, что различают несколько безрисковых ставок: глобальную безрисковую ставку и локальную безрисковую ставку.
Глобальная безрисковая ставка – ставка по государственным облигациям США, Англии, Германии и Швейцарии. (Информацию по американским государственным облигациям можно найти тут). В качестве глобальной безрисковой ставки доходности правильнее выбирать ставку доходности по 10-летним американским государственным облигациям.
Локальная безрисковая ставка – ставка по российским государственным облигациям номинированным в рублях (данные о ставке можно посмотреть здесь).
Среднерыночная доходность (Rm) представляет собой доходность рыночного портфеля. В качестве данного показателя берут, например, среднюю доходность по акциям, включенным в рыночный портфель, используемый для расчета какого-либо общеизвестного индекса (Индекс ММВБ, Nikkei 225 и т.п.), данные значения легко можно найти в открытом доступе.
Безрисковая доходность (Rf) представляет собой, ожидаемый среднегодовой темп прироста экономики в долгосрочной перспективе, но с поправкой на изменение краткосрочной ликвидности и инфляцию. Единого мнения в отношении значения показателя нет. Так, американские финансовые аналитики полагают, что в качестве доходности безрисковых активов следует брать доходность по казначейским обязательствам, но вот какие обязательства использовать долго- или краткосрочные, – единства нет.
Разницу между среднерыночной нормой доходности акций и безрисковой ставкой (Rм — Rf) называют премией за риск вложения в акции (equity risk premium, ERP).
Размер премии за риск инвестирования в акционерный капитал, ERP. В качестве ERP можно взять готовую цифру из верифицированного источника аналитических данных. К примеру для России, на 01.01.2015 ERP составлял 13,72%, а для западных компаний обычно эта премия варьируется в диапазоне 3,5% — 6%.
Бета-коэффициент характеризует чувствительность оцениваемой ценной бумаги к изменениям рыночной доходности (рассчитывается по статистическим данным и выражает вариабельность доходности ценной бумаги по отношению к среднерыночной доходности – доходности того или иного фондового индекса).
β-коэффициент выражает меру систематического риска для акций компании. Величина коэффициента определяется на основе анализа ретроспективных данных соответствующими статистическими службами фирм, специализирующихся на рынке информационно-аналитических услуг, инвестиционными и консалтинговыми компаниями и публикуется в финансовых справочниках и периодических изданиях, анализирующих фондовые рынки. Общий алгоритм расчета показателя в следующей таблице:
Общий алгоритм расчета показателя
| № п/п | Локальный β (долл.) | Локальный β (руб.) |
|---|---|---|
| 1 | Стандартное отклонение доходности RTSI | Стандартное отклонение доходности ММВБ |
| 2 | Стандартное отклонение доходности конкретного эмитента | Стандартное отклонение доходности конкретного эмитента |
| 3 | Корреляция доходностей RTSI и акций конкретного эмитента | Корреляция доходностей ММВБ и акций конкретного эмитента |
| 4 | Бета-коэффициент = стр. 2 x стр. 3 / стр. 1 | |
Отметим, информацию о бета-коэффициенте публичных компаний можно взять в виде готовой цифры из открытых источников, к примеру, для акций ГМК «Норильский никель» на 25.12.15 значение коэффициента равно 0,88.
Если необходимо рассчитать значение бета-коэффициента для непубличной компании, то можно воспользоваться формулой Хамады [6]:
Рассмотрим пример расчета бета-коэффициента для непубличной компании, занимающейся производством пищевых продуктов (скачать).
Известны достаточно простые алгоритмы, позволяющие найти приблизительное значение бета-коэффициента для данной ценной бумаги. Пусть Kij — доходность акций i-й компании в j-м году, a Kmj — доходность на рынке в среднем (j = 1, 2, . n) за все анализируемые периоды. Если к рынку применима модель САРМ, то, как следует из модели, β-коэффициент представляет собой коэффициент эластичности, а его значение можно рассчитать как отношение приращения доходности акций i-й компании (ΔKij) к приращению среднерыночной доходности (ΔKmj):
Алгоритм, задаваемый формулой, весьма приблизителен, поскольку приращения можно считать различными способами. Достаточно часто используется следующий вариант расчета β:
- определяются средние (например, по годам) значения доходности акций данной компании и по рынку в целом;
- строится уравнение линейной регрессии, отражающее зависимость средней доходности акций данной компании от доходности на рынке в среднем;
- коэффициент регрессии (т.е. коэффициент при параметре Km) и будет бета-коэффициентом.
Так как данные для расчета CAPM базируются на процентных ставках номинированных в долларах США, то при использовании рублевых денежных потоков необходимо скорректировать полученную величину ставки дисконтирования по следующей формуле:
где,
Rrur — ставка дисконтирования, номинированная в рублях;
Rusd — ставка дисконтирования, номинированная в долларах США;
Brur — доходность по рублевым государственным облигациям России;
Busd — доходность по еврооблигациям России, номинированным в долларах США.[4]
Одним из основных преимуществ в применении модели является то что, модель CAРM позволяет учесть влияние внешних факторов, не зависящих от хода реализации проекта, – страновые и политические риски, ставки доходности (без рисковые, отраслевые и среднерыночные). При этом, правда, следует учитывать и ее недостатки, к которым можно отнести:
- Имеет прямое отношение только к компаниям, которые являются открытыми акционерными обществами и, следовательно, их акциями торгуют на фондовых рынках.
- Вызывает затруднения при определении, какие из вложений можно считать без рисковыми, применим только к компаниям, которые располагают достаточной статистикой для расчета своего коэффициента бета или имеют возможность найти компанию-аналог, чей коэффициент бета мог бы использоваться в расчетах.
При использовании в модели информации зарубежных фондовых рынков в ставке дисконта необходимо учитывать дополнительный риск, связанный с инвестированием средств в Россию (страновой риск). Уровень риска инвестирования в конкретную страну определяется крупнейшими информационно-аналитическими и рейтинговыми агентствами.
Capital Asset Pricing Model, САРМ – центральная концепция современной финансовой экономики. Эта модель дает представление о том, какое должно быть соотношение между риском вложения в актив и доходностью этого вложения. Эта формула нашла широкое применение в теории современного инвестиционного анализа в самых различных его областях: оценки прибыльности проектов, портфельных инвестиций, оценки предприятий.
Источник