Модель доходности финансовых активов описывает зависимость между

Модели оценки доходности финансовых активов

X. Финансовый менеджмент

Модель оценки доходности финансовых активов (САРМ) описывает зависимость между рыночным риском и требуемой доходностью. САРМ базируется на допущениях идеального рынка, на добавлении к допустимому множеству портфелей безрискового актива. Линия рынка капитала отражает зависимость риск-доходность для эффективных портфелей, то есть для портфелей, сочетающих рисковые и безрисковые активы. Линия рынка ценных бумаг отражает зависимость риск-доходность для отдельных акций. Требуемая доходность любой акции равна безрисковой норме, сложенной с произведением премии за рыночный риск и b — коэффициента акции. Формула определения требуемой инвесторами доходности финансового инструмента имеет вид:

r_f – безрисковый уровень доходности (risk free);

r_m – среднерыночный уровень доходности.

Коэффициент регрессии β служит количественным измерителем систематического риска, не поддающегося диверсификации. Ценная бумага, имеющая β-коэффициент, равный 1, копирует поведение рынка в целом. Если значение коэффициента выше 1, реакция ценной бумаги опережает изменение рынка как в одну, так и в другую сторону. Систематический риск такого финансового актива выше среднего. Менее рисковыми являются активы, β-коэффициенты которых ниже 1 (но выше 0). Концепция β-коэффициентов составляют основу модели оценки финансовых активов (Capital Assets Pricing Model, CAPM). При помощи этого показателя может быть рассчитана величина премии за риск, требуемой инвесторами по вложениям, имеющим систематический риск выше среднего.

Считается, что инвесторы питают неприязнь к излишнему на их взгляд риску, поэтому любая ценная бумага, отличная от безрисковых государственных облигаций или казначейских векселей, может рассчитывать на признание инвесторов только в том случае, если уровень ее ожидаемой доходности компенсирует присущий ей дополнительный риск. Данная надбавка называется премией за риск напрямую зависит от величины β-коэффициента данного актива, так как предназначена для компенсации только систематического риска. Несистематический риск может быть устранен самим инвестором путем диверсификации своего портфеля, поэтому рынок не считает нужным устанавливать вознаграждение за этот вид риска.

Сама по себе CAPM является изящной научной теорией, имеющей солидное математическое обоснование. Для того, чтобы она “работала” необходимо соблюдение таких заведомо нереалистических условий как наличие абсолютно эффективного рынка, отсутствие трансакционных издержек и налогов, равный доступ всех инвесторов к кредитным ресурсам и др. Тем не менее столь абстрактное логическое построение получило практически всеобщее признание в мире реальных финансов. Крупнейшие рыночные институты, такие как инвестиционный банк Merril Lynch, регулярно рассчитывают β-коэффициенты всех крупных компаний, котирующихся на фондовых биржах. Отсутствие в России сформированной финансовой инфраструктуры пока еще препятствует использованию всего потенциала, заложенного в данную модель.

В качестве альтернативы традиционной однофакторной модели САРМ можно назвать модель арбитражного ценообразования (Arbitrage Pricing Model, АРМ). В основе модели утверждение о том, что рисковая доходность определяется многими экономическими факторами (рыночная ситуация в стране, стабильность мировой экономики, инфляция, динамика процентных ставок и т.д.). Таким образом, модель должна включать множество факторов и в наиболее общем виде описывается зависимостью:

λ_j – требуемая доходность портфеля с единичной чувствительностью к j-му экономическому фактору (b_j = 1) и нулевой чувствительностью (b_j = 0), к другим факторам; е_i – влияние не включённых в модель специфических факторов на изменение доходности i-й ценной бумаги; b_ij – чувствительность доходности i-го актива к j-му фактору.

Данная модель обладает достоинствами и недостатками. Основным недостатком является то, что она не предусматривает жёстких исходных предпосылок, которые свойственны модели САРМ, количество и состав релевантных факторов определяются аналитиком и заранее не регламентируются. Фактическая реализация модели связана с использованием сложного процесса математической статистики. Тем не менее, главное достоинство этой теории в том, что доходность является функцией многих переменных и рассматривается среди учёных как одна из перспективных.

Источник

Модель доходности финансовых активов (САМР)

Модель САМР описывает зависимость между рыночным риском и требуемой доходностью при определенных условиях (инвесторы ведут себя рационально, измеряют время в одних единицах, мыслят сходным образом, заимствуют и предоставляют средства в долг под безрисковую ставку и др.). При соблюдении указанных допущений инвестиционный портфель, повторяющий пропорции рынка, должен быть оптимальным инвестиционным решением для всех инвесторов. 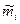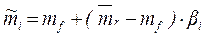Логика данной модели построена на том, что решение о вложении инвестиций принимается с учетом двух факторов — ожидаемой доходности и риска, мерой которого является дисперсия или стандартное отклонение доходности. Итоговое уравнение данной модели имеет следующий вид:

, (5.11)

где 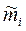— ожидаемый доход на ценную бумагу i при равновесии рынка;

m_f— ставка дохода на безрисковую ценную бумагу (например, гаранти­рованные ценные бумаги с фиксированным доходом в виде государственных облигаций).

b _i — коэффициент акции i – является мерой рыночного риска акции (измеряет изменчивость доходности акции по отношению к доходности среднерыночного портфеля). Он определяет угол наклона характеристической линии акции, построенной по статистическим данным о доходности i-й акции и среднерыночной доходности.

– рыночная премия за риск.

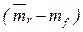
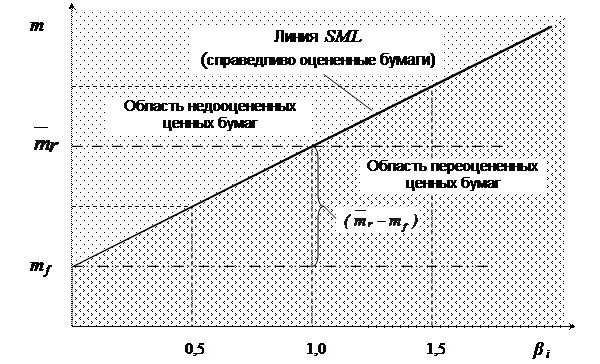
Выражение (5.11) описывает линейную связь между доходом ценной бумаги и ее бета-коэффициентом и его называют уравнением линии рынка ценных бумаг (SML). Графическое изображение линии SML приведено на рис. 5.5.

Рис.5.5. Общий вид графика линии рынка ценных бумаг SML

Линия SML отражает идеальную зависимость между β и эффективностью бумаг и портфелей. Все точки, лежащие на прямой SML, соответствуют «справедливо» оцененным бумагам (портфе­лям). Над линией находится область недооцененных ценных бумаг, а под линией – область переоцененных.

Линия рынка ценных (SML) бумаг отражает зависимость риск – доходность для отдельных акций. Требуемая доходность любой акции равна безрисковой норме m_f, сложенной с произведением премии за рыночный риск 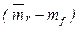и b — коэффициента акции:

Отсутствие риска по безрисковым ценным бумагам влечет за собой и мини­мальный уровень прибыли. В силу этого безрисковые бумаги являются главным регулятором прибылей и рисков.

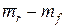
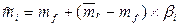
По данным Э. Димсона (полученным на основе анализа фондовых рынков за 50 лет), в экономически развитых странах мира рыночная премия ( ) составляет 8% годовых. Например, при ставке безрискового вложения (в долларах) равной 5% годовых и коэффициенте b для некоторой компании равном 0,65, инвестор в условиях устойчивой экономики должен потребовать от акций данной компании долгосрочную доходность в размере:

= 5% + 8% x 0,65 = 10,2% годовых, долл.

Но на развивающихся рынках (в том числе и фондовый рынок России) подобные оценки могут оказаться неправомерными.

Величины коэффициентов «бета» в модели САРМив рыночной модели сходны по смыслу, но рыночная модель в отличие от САРМ не является моделью равновесия финансового рынка. Кроме того, рыночная модель использует рыночный индекс, который в общем случае не охватывает рыночный портфель, используемый в САРМ.

Существует ряд причин, по которым требуемая и ожидаемая доходности не совпадают: 1) изменение безрисковой ставки ввиду пересмотра ожидаемого темпа инфляции, 2) изменение b, 3) переоценка отношения инвеcтo-pa к риску.

Модель САРМ хорошо обоснована с позиции теории, но она не может быть подтверждена эмпирически, еепараметры с трудом поддаются оценке и поэтому ее применение на практике ограничено.

Для преодоления недостатков САРМ разработаны альтернативные модели риск – доходность. Наиболее перспективной из новых моделей построена на теории арбитражного ценообразования (Arbitrage Pricing Theory, АРТ). основы которой были сформулированы американским экономистом Жераром Дэбре, получившего Нобелевскую премию по экономике за новые подходы к общей теории экономического равновесия.

Источник

Модель оценки доходности финансовых активов САРМ

Модель описывает зависимость рыночного риска и доходности финансовых активов. Теория САРМ (Capital Assets Pricing Model)была разработана Уильямом Ф. Шарпом и опубликована им в 1964 году. Он получил нобелевскую премию по экономике за исследования в области ценообразования финансовых активов.

Модель основана на предпосылках о существовании идеальных рынков капитала.

1. Главная цель инвестора – максимизация прироста своего достояния.

2. Все инвесторы могут давать и брать ссуды неограниченного размера по безрисковой процентной ставке.

3. Ожидания инвесторов относительно изменений показателей акций одинаковы.

4. Все активы абсолютно делимы и совершенно ликвидны.

5. Не существует трансакционных затрат.

6. Не учитываются налоги.

7. Инвесторы предполагают, что их деятельность не влияет на уровень цен.

8. Количество финансовых активов заранее определено и фиксировано.

Оптимальный выбор инвестора определяется как пересечение кривых безразличия, отражающих предпочтения данного инвестора, и совокупности эффективных портфелей, которые могут быть сформированы на данном рынке. Предполагалось, что все активы, входящие в оптимальный портфель – рисковые. Тем не менее, можно выделить безрисковые финансовые активы – те, по которым нет риска дефолта, такими активами принято считать государственные ценные бумаги (в условиях стабильности государственного финансового рынка и государственных финансов в целом). Если инвестор включит в портфель безрисковые активы это приведет к изменению структуры портфеля и именит его окончательный инвестиционный выбор, выражающийся в структуре оптимального портфеля.

Ллиния рынка капитала – CML –это касательная от точки K_rf, характеризующей безрисковый актив (его доходность K_rf, риск s = 0) к эффективному множеству портфелей.

Определим доходность и риск оптимального портфеля ценных бумаг (M), сформированного из безрискового актива и совокупности рисковых активов.

Доходность портфеля К_р можно определить по формуле:

K_rf — доходность безрискового актива,

х – доля безрискового актива в портфеле,

K_M — доходность портфеля, состоящего из рисковых активов.

Уровень риска s_р портфеля может быть определен, как его СКО, для расчетов можно воспользоваться формулой:

s_р – СКО доходности портфеля,

s_м – СКО доходности портфеля, состоящего только из рисковых активов,

х – доля безрисковых активов в портфеле.

Степень наклона (крутизны) CML показывает, какую доходность могут получить инвесторы в зависимости от принятых рисков, ее можно рассчитать следующим образом: (K_М — K_rf )/s_м. Эта величина отражает рыночную цену полностью диверсифицированных портфелей.

Рисковость ценной бумаги определяется ее бета-коэффициентом. Этот коэффициент характеризует изменчивость доходности конкретной ценной бумаги относительно доходности рынка ценных бумаг.

Предполагается, что некоторая «средняя» акция имеет b-коэффициент равный 1. Если изменчивость доходности данной ценной бумаги меньше, чем у «средней» акции, то ее b-коэффициент меньше единицы.

Связь между риском и доходностью конкретной ценной бумаги называют уравнением линии рынка ценных бумаг – SML. Оно выглядит следующим образом: K_i = K_rf + (K_М — K_rf )*b_i

K_i – требуемая доходность i-ой акции,

K_rf — доходность безрискового актива,

K_M — доходность рыночного портфеля,

b_i — b-коэффициент i-ой акции.

(K_М — K_rf )-рыночная премия за риск или цена риска для средней акции.

На требуемый уровень доходности влияет инфляция, но она одинаково сказывается на всех ставках доходности. В каждой из этих номинальных ставок можно выделить две составляющих:

— реальный уровень доходности,

Крутизна линии рынка ценных бумаг отражает отношение инвесторов к риску: чем круче наклон, тем меньше инвесторы склонны к риску.

Рассмотрим основные различия CML и SML:

1. Для линии рынка капитала риск характеризуется СКО – показатель общего риска. Для линии рынка ценных бумаг показателем риска является бета-коэффициент – показатель специфиического риска.

2. При равновесии только полностью диверсифицированные портфели находятся на линии рынка капитала, а отдельные ценные бумаги лежат под ней. Все ценные бумаги и все портфели находятся на линии рынка ценных бумаг.

Как уже было сказано, предполагается, что некоторая «средняя» акция имеет b-коэффициент равный 1. Характеристики этой «средней» акции будут меняться в зависимости от изменения рыночной ситуации. При изменении ситуации на рынке показатели «средней» акции меняются в том же направлении и на ту же величину. b-коэффициент большинства рыночных акций меняется от 0,75 до 1,5.

Например, b-коэффициент “Procter&Gambel” равен 1, “Harley-Davidson” – 1,6.

b-коэффициент портфеля ценных бумаг рассчитывается по формуле средней арифметической взвешенной.:

, где

х_i – доля i-ой ценной бумаги в портфеле,

Если в портфель добавляются ценные бумаги, имеющие b>1, то уровень риска портфеля повышается, и, наоборот, если добавляются ценные бумаги, имеющие b * + (F₁ – F₁ * )*b_i1 +…+(F_j – F_j * )*b_ij +e_i , где

K_i – фактическая доходность i-ой акции,

K_i * – ожидаемая доходность i-ой акции,

F_j — фактическое значение экономического фактора j,

F_j * — ожидаемое значение экономического фактора j,

b_ij — влияние чувствительности акции i к экономическому фактору j,

e_i — влияние специфических факторов на изменение фактической доходности акции i.

Концепция арбитражного ценообразования использует меньшее количество допущений, чем САРМ и более детально учитывает влияние внешней среды. Но теория имеет существенный недостаток, в ней нет ограниченного списка факторов, поэтому невозможно учесть влияние полностью, всегда останутся факторы, которые влияют на фактическую доходность акций, но не были учтены при анализе. Кроме того, возможно, что влияние неучтенного фактора достаточно сильно, чтобы рассматривать полученные без его учета результаты, как достоверные.

Концепция арбитражного ценообразования развивается и, возможно, в будущем основные недостатки модели будут учтены за счет внесения в модель корректив.

Вопросы и задачи к главе 3

1. В чем состоит анализ дисконтированного денежного потока? Перечислите его основные этапы.

2. Какой основной вывод был сделан М. Миллером и Ф. Модильяни при анализе структуры капитала фирмы?

3. Какое влияние в условиях идеальных рынков, по мнению М. Миллера и Ф. Модильяни оказывает политика выплаты дивидендов на стоимость фирмы?

4. Как можно снизить совокупный риск инвестора согласно теории портфеля?

5. Функцией каких переменных является требуемая доходность рисковых активов согласно теории САРМ?

6. Что понимается под «эффективностью» в гипотезе эффективности рынков? Охарактеризуйте основные формы эффективности.

7. Какие показатели связывает модель САРМ?

8. Перечислите основные предпосылки модели САРМ?

9. В чем сходства и различия линии рынка капитала и линии рынка ценных бумаг?

10. Что такое безрисковый финансовый актив?

11. Что такое бета-коэффициент? Почему бета-коэффициент «средней акции» равен 1?

12. Как влияет на риск портфеля добавление в него ценных бумаг бета-коэффициент которых больше 1? меньше 1?

13. Каково практическое значение модель САРМ?

14. В чем основное отличие теории арбитражного ценообразования от САРМ?

15. Назовите основные достоинства и недостатки теории арбитражного ценообразования.

Задачи

1. Определите доходность портфеля, состоящего на 30% из безрискового актива, доходностью 15% и из рисковых ценных бумаг, объединенных в портфель с общим уровнем доходности 25%.

2. Определите уровень риска портфеля, состоящего на 30% из безрискового актива, доходностью 15% и из рисковых ценных бумаг, СКО которых составляет 20.

3. Определите требуемую доходность акции, если известно что доходность безрискового актива 10%, доходность рыночного портфеля 18%, а бета-коэффициент акции равен 1,3. Чему будет равна требуемая доходность той же акции, если ее бета коэффициент составит 1,8.

4. Акция Х имеет коэффициент бета, равный 1,3; безрисковая доходность составляет 8%, премия за рыночный риск – 7%. какова требуемая норма прибили по акции Х.

5. Определите бета-коэффициент портфеля ценных бумаг, состоящего из акций фирмы «Ромашка» на сумму 30 тыс. руб., бета-коэффициент акций равен 1,2; акций фирмы «Георгин» на сумму 50 тыс. руб., бета-коэффициент акций равен 1,6; акций фирмы «Тюльпан» на сумму 20 тыс. руб., бета-коэффициент акций равен 0,8. Сравните уровень риска портфеля со среднерыночным.

1. Базовый курс по рынку ценных бумаг. – М, ИАУУ НАУФОР — 1999

2. Басовский Л.Е. Финансовый менеджмент. – М.: Инфра-М, — 2002;

3. Бригхем Ю., Гапенски Л. Финансовый менеджмент. — СПб.: Экономическая школа, 1997;

4. Касимов Ю.Ф.Основы теории оптимального портфеля ценных бумаг. – М.: Филинъ, 1998. – 142 с.;

5. Колб Р.Б., Родригес Р. Дж. Финансовый менеджмент. – М.: Издатество «Финпресс»,2001;

6. Лытнев О. Курс лекций «Основы финансового менеджмента» — 2000, http://www. cfin.ru

7. Станиславчик Е.Н. Основы финансового менеджмента. – М.: «Ось-89»,2001.

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначен­ные для поддерживания проводов на необходимой высоте над землей, водой.

Источник