Mirr irr npv инвестиции

Инвестиционные показатели NPV, IRR: Excel на службе у финансового директора

Как рассчитать NPV и IRR, оценить эффективность инвестиционных проектов, рассчитать сумму аннуитета и проверить банк на честность. Финансовых формул в Excel много. Часть из них предназначена для расчета амортизации разными способами. Другие – для определения стоимости ценных бумаг. Третьи для чего-то еще. Здесь мы разберем самые главные и «животрепещущие» (на мой взгляд).

Это формулы, которые позволят рассчитать:
— NPV (Net Present Value) — чистую приведенную стоимость.
— IRR (Internal Rate of Return) — внутреннюю ставку доходности.
— Аннуитеты – равномерные платежи.

Также рассмотрим некоторые нюансы использования этих формул. Все расчеты можно найти в приложенном файле. Основной акцент сделан на функции Excel, поэтому саму финансовую математику разбирать особо не будем.

Оценка целесообразности проекта с помощью NPV

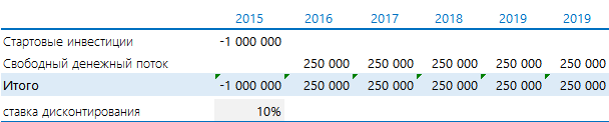
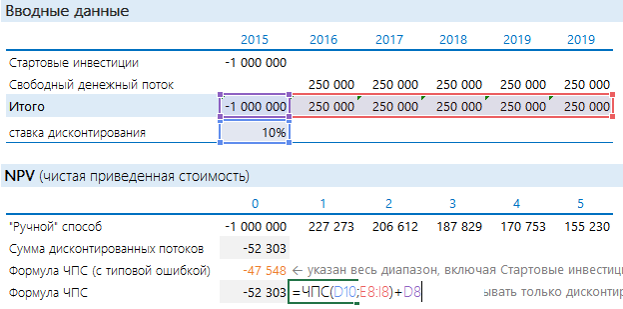
Есть проект, который ежегодно в течении 5 лет будет приносить 250 000 руб. Нужно потратить 1 000 000 руб. Предположим, что ставка дисконтирования равна 10%.

Оцениваем NPV проекта. Напомню формулу этого показателя:

Если денежные потоки, приведенные к текущему периоду, больше инвестированных денег (NPV > 0), то проект выгодный. В противном случае – нет. Другими словами, нам потребуется сделать в Excel следующее:

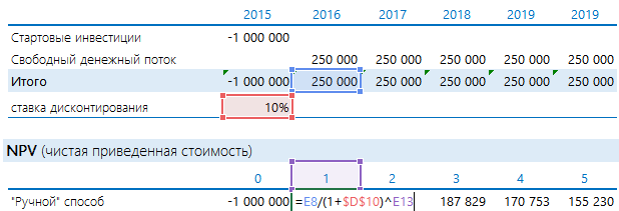
Добавить порядковые номера лет: 0 – стартовый год, к нему приводятся потоки. 1, 2, 3 и т.д. – это годы реализации проекта. В формуле на рисунке выполнены действия, которые прописаны выше после знака суммы (Σ): денежный поток за период делится на сумму 1 и ставки дисконтирования, возведенную в степень соответствующего года.

Рассчитанная строка представляет собой дисконтированный денежный поток. Чтобы получить значение NPV, достаточно найти общую сумму всей строки.

Получается «-52 303». Проект невыгоден.

Чтобы определить NPV, на самом деле необязательно готовить такую таблицу. Достаточно воспользоваться формулой Excel ЧПС. Синтаксис формулы такой (здесь и далее будет написано не как в справке Excel, а в переводе на понятный язык):

ЧПС(Ставка дисконтирования; Диапазон дисконтируемых значений)

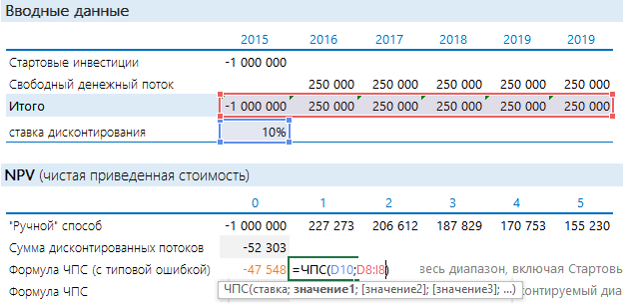
То есть достаточно указать ячейку с процентом и с денежными потоками. Но при использовании этой формулы с непривычки финансисты часто допускают ошибку:

Вообще-то дисконтированный поток и расчет по ЧПС должны совпадать. Почему же здесь разные значения? Дело в том, что ЧПС начинает дисконтировать с первого же значения. Т.е. она на самом деле ищет приведенную стоимость. А стартовые инвестиции нужно отнимать после. Правильная запись формулы в нашем случае будет иметь следующий вид:

Стартовые инвестиции «выведены» за пределы дисконтируемого диапазона и вычтены: т.к. стартовые инвестиции уже идут с минусом, то D8 нужно прибавлять. Теперь результаты одинаковые.

Оценка целесообразности проекта с помощью IRR

Как еще можно оценить проект? Можно посмотреть на него с точки зрения ставки дисконтирования. Задать вопрос: а какая должна быть ставка, чтобы NPV стала = 0? Вот этой ставкой как раз и является IRR. Если Ставка дисконтирования
Аннуитеты – любимая банковская цифра

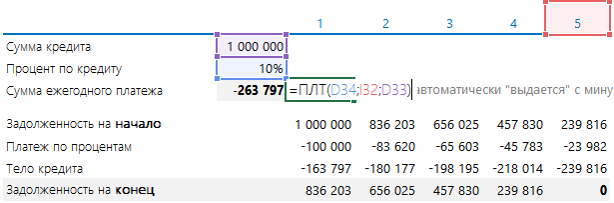
Сначала поговорим о волнующем вопросе – как банки рассчитывают сумму равномерного платежа, как их проверить и как это понимать. Допустим, вы собираетесь взять кредит 1 000 000 руб. на 5 лет под 10% годовых. Платить будете раз в год равными платежами. Формулу из учебника по финансовому менеджменту здесь приводить не будем. Приведем формулу Excel:

ПЛТ(Ставка дисконтир; Количество периодов; Сумма кредита которую вы берете)

В формуле есть еще два необязательных пункта: сумма, которая должна остаться (по умолчанию ноль), и как высчитывать сумму – на начало месяца, и тогда ставят 1, или на конец – ставят ноль. В 90% случаев эти пункты не нужны, поэтому их можно не ставить вообще. Итого аннуитет определяется так:

Сумма ежегодного платежа получается сразу с минусом. Эту сумму нужно каждый год платить банку.

В ней содержатся две части: 1) платеж по кредиту, 2) тело кредита.

Ниже они показаны. Платеж по кредиту берется как 10% (процент по кредиту) от суммы задолженности на начало периода. Тело – как разность между ежегодным платежом и платежом по процентам (в Excel можно найти формулы, которые рассчитают вам и эти платежи). Задолженность на конец рассчитывается как разность между Задолженностью на начало и платежом по телу кредита.

Если платежи не ежегодные, а ежемесячные или ежеквартальные, то нужно ставку и период приводить к этим значениям. Так если бы у нас платеж был каждый месяц, формула выглядела бы так:

Мы бы годовую ставку разделили на 12 (привели к ежемесячному), и взяли не 5 периодов, а 5 • 12 = 60 месяцев. И получили ежемесячный платеж в 21 247 руб.

Нюансы и тонкости

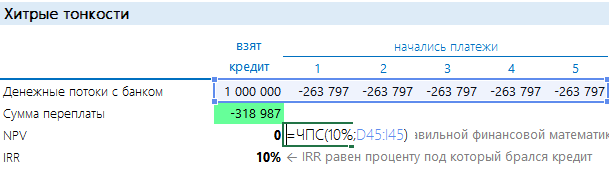
А теперь обсудим, как проверять банки на честность. Любой поток платежей по кредиту подразумевает под собой, что все выбытия денег приведены к поступлениям на ставку кредитования. Теперь по-русски: если мы построим денежный поток из полученного нами кредита и последующих наших аннуитетных платежей, то затем мы можем посчитать по ним NPV и IRR. NPV при этом должно принять нулевое значение, а IRR, что интереснее, — показать нам реальную процентную ставку.

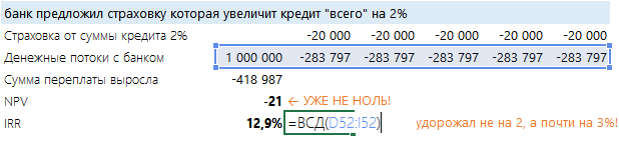
Когда кредит и платежи по нему рассчитаны правильно, то NPV, взятый по той же процентной ставке, равен нулю. А IRR показывает ставку. Когда банк делает предложение, от которого невозможно отказаться и которое увеличит кредитную ставку «всего» на несколько процентов – не верьте и пересчитывайте! Например, в нашем случае банк предложил страховку «всего» 2 % от суммы кредита в год. Думаете это прирост всего в 2%? Нет! Дело в том, что настоящий кредит в начале каждого года уменьшается:

В результате видно, что NPV не равен нулю. А реальный процент не 10, а 12,9%! Обратите внимание: здесь же выросла сумма переплаты. Если вас это смутит, вам могут предложить «еще более выгодные условия» — заплатить переплату сейчас, а остальное потом, меньшими платежами, или в нашем примере просто заплатить больше, а потом меньше. Сумма переплаты не изменится, а вот процент…

Что здесь сделано? Из каждого последующего платежа взята сумма 43 797 руб. и добавлена к первому же платежу (а бывает выкручивают сумму в момент выдачи кредита). Если для реального сектора финансовая математика «деньги вчера – деньги завтра» кажется несколько отдаленной от жизни, для банков это реальная прибыль. Поэтому всеми силами нагружают первый платеж. А вы с помощью простых формул сможете подготовить основу для дальнейших переговоров.

Да, не забудьте, если речь идет про ежемесячные платежи, умножать на 12.

Источник

Модифицированная внутренняя норма доходности (MIRR)

Что такое модифицированная внутренняя норма доходности (MIRR)?

Модифицированная внутренняя норма прибыли (MIRR) предполагает, что положительные денежные потоки реинвестируются за счет стоимости капитала фирмы и что первоначальные затраты финансируются за счет финансовых затрат фирмы. Напротив, традиционная внутренняя норма доходности (IRR) предполагает, что денежные потоки от проекта реинвестируются по самой IRR. Таким образом, MIRR более точно отражает стоимость и прибыльность проекта.

Формула и расчет MIRR

С учетом переменных формула MIRR выражается как:

Между тем, внутренняя норма прибыли (IRR) – это ставка дисконтирования, которая делает чистую приведенную стоимость (NPV) всех денежных потоков от конкретного проекта равной нулю. При расчетах MIRR и IRR используется формула NPV.

Ключевые выводы

• MIRR улучшает IRR, предполагая, что положительные денежные потоки реинвестируются за счет стоимости капитала фирмы.
• MIRR используется для ранжирования инвестиций или проектов, которые может предпринять фирма или инвестор.
• MIRR предназначен для создания одного решения, устраняя проблему нескольких IRR.

Что вам может сказать MIRR

MIRR используется для ранжирования инвестиций или проектов неравного размера. Расчет – это решение двух основных проблем, которые существуют в популярном расчете IRR. Первая основная проблема с IRR заключается в том, что для одного и того же проекта можно найти несколько решений. Вторая проблема заключается в том, что предположение о том, что положительные денежные потоки реинвестируются по IRR, на практике считается нецелесообразным. С MIRR существует только одно решение для данного проекта, и норма реинвестирования положительных денежных потоков намного более актуальна на практике.

MIRR позволяет руководителям проектов изменять предполагаемую скорость реинвестированного роста от этапа к этапу проекта. Наиболее распространенный метод – ввести среднюю предполагаемую стоимость капитала, но есть возможность добавить любую конкретную ожидаемую ставку реинвестирования.

Разница между MIRR и IRR

Несмотря на то, что показатель внутренней нормы прибыли (IRR) популярен среди бизнес-менеджеров, он имеет тенденцию завышать прибыльность проекта и может привести к ошибкам при планировании капитальных вложений, основанных на чрезмерно оптимистичной оценке. Модифицированная внутренняя норма доходности (MIRR) компенсирует этот недостаток и дает менеджерам больше контроля над предполагаемой ставкой реинвестирования из будущего денежного потока.

Расчет IRR действует как инвертированная скорость роста сложного процента. Он должен дисконтировать рост от первоначальных инвестиций в дополнение к реинвестированным денежным потокам. Однако IRR не дает реалистичной картины того, как денежные потоки фактически возвращаются в будущие проекты.

Денежные потоки часто реинвестируются за счет капитала, а не по той же ставке, по которой они были созданы изначально. IRR предполагает, что темпы роста остаются постоянными от проекта к проекту. С помощью базовых показателей IRR очень легко переоценить потенциальную будущую стоимость.

Еще одна серьезная проблема с IRR возникает, когда у проекта разные периоды положительных и отрицательных денежных потоков. В этих случаях IRR дает более одного числа, вызывая неопределенность и путаницу. MIRR также решает эту проблему.

Разница между MIRR и FMRR

Курс финансового управления возврата (FMRR) является метрическим наиболее часто используется для оценки эффективности инвестиций в недвижимость и относится к инвестиционной недвижимости доверия (REIT). Модифицированная внутренняя норма доходности (MIRR) улучшает значение стандартной внутренней нормы доходности (IRR) за счет корректировки различий в предполагаемых нормах реинвестирования первоначальных денежных затрат и последующих денежных поступлений. FMRR делает еще один шаг вперед, определяя отток и приток денежных средств по двум различным ставкам, известным как «безопасная ставка» и «ставка реинвестирования».

Безопасная ставка предполагает, что средства, необходимые для покрытия отрицательных денежных потоков, приносят проценты по легко достижимой ставке и могут быть сняты при необходимости в любой момент (например, в течение дня после внесения депозита). В этом случае скорость является «безопасной», потому что средства являются очень жидкими и безопасно доступны с минимальным риском, когда это необходимо.

Ставка реинвестирования включает ставку, которая будет получена, когда положительные денежные потоки реинвестируются в аналогичные промежуточные или долгосрочные инвестиции с сопоставимым риском. Ставка реинвестирования выше, чем безопасная ставка, потому что она неликвидна (т. Е. Относится к другим инвестициям) и, следовательно, требует более высокой ставки дисконтирования.

Ограничения использования MIRR

Первое ограничение MIRR заключается в том, что для принятия решения вам необходимо вычислить оценку стоимости капитала, расчет, который может быть субъективным и варьироваться в зависимости от сделанных предположений.

Как и в случае с IRR, MIRR может предоставить информацию, которая приводит к неоптимальным решениям, которые не максимизируют ценность, когда одновременно рассматриваются несколько вариантов инвестирования. MIRR фактически не дает количественной оценки различных воздействий различных инвестиций в абсолютном выражении; NPV часто обеспечивает более эффективную теоретическую основу для выбора взаимоисключающих инвестиций. Это также может не дать оптимальных результатов в случае нормирования капитала.

MIRR также может быть трудно понять людям, не имеющим финансового образования. Более того, теоретическая основа MIRR также оспаривается среди ученых.

Пример использования MIRR

Базовый расчет IRR выглядит следующим образом. Предположим, что двухлетний проект с первоначальными затратами 195 долларов и стоимостью капитала 12% принесет 121 доллар в первый год и 131 доллар во второй год. Чтобы найти IRR проекта таким образом, чтобы чистая приведенная стоимость (NPV) = 0 при IRR = 18,66%:

NпVзнак равно0знак равно-195+121(1+ярр)+131(1+ярр)2ЧПС = 0 = -195 + \ frac <121> <(1 + IRR)>+ \ frac <131><(1 + IRR) ^ 2>NPVзнак равно0знак равно-195+(1+IRR)

Чтобы рассчитать MIRR проекта, предположим, что положительные будущая стоимость положительных денежных потоков при t = 2 рассчитывается как:

Затем разделите будущую стоимость денежных потоков на приведенную стоимость первоначальных затрат, которая составляла 195 долларов, и найдите геометрическую прибыль за два периода. Наконец, скорректируйте это соотношение для периода времени, используя формулу для MIRR, учитывая:

Mяррзнак равно$266.52$1951/2-1знак равно1.1691-1знак равно16.91%MIRR = \ frac <\ $ 266,52> <\ $ 195>^ <1>– 1 = 1,1691 – 1 = 16,91 \%MIRRзнак равно195долларов США

В этом конкретном примере IRR дает слишком оптимистичную картину потенциала проекта, в то время как MIRR дает более реалистичную оценку проекта.

Источник