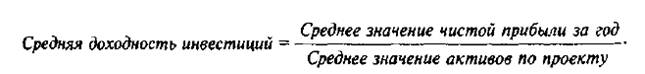Метод средней бухгалтерской доходности

Курс лекций «Основы финансового менеджмента»

5.2. Определение средней доходности

В практике финансовых расчетов часто возникает необходимость расчета средней доходности набора (портфеля) инвестиций за определенный период или средней доходности вложения капитала за несколько периодов времени (например, 3 квартала или 5 лет). В первом случае используется формула среднеарифметической взвешенной , в которой в качестве весов используются суммы инвестиций каждого вида. Вернемся к примеру из предыдущего параграфа с вложением 1000 рублей в два вида деятельности: торговую и финансовую. Можно сказать, что владелец этих денег сформировал инвестиционный портфель, состоящий из двух инструментов – инвестиции в собственный капитал магазина и финансовые (спекулятивные) инвестиции. Сумма каждого из вложений составила 500 рублей. Доходность по первому направлению вложений составила 10%, по второму – 40% годовых. Применив формулу средней арифметической (в данном случае, ввиду равенства весов, можно использовать среднюю арифметическую простую) получим среднюю доходность инвестиций за год, равную 25% ((10 + 40) / 2). Она в точности соответствует полной доходности “портфеля”, рассчитанной в предыдущем параграфе. Если бы владелец изменил структуру своих инвестиций и вложил в торговлю только 300 рублей (30%), а в финансовые спекуляции 700 рублей (70%), то при неизменных уровнях доходности каждого из направлений средняя доходность его “портфеля” составила бы 31% (10 * 0,3 + 40 * 0,7). Следовательно, общую формулу расчета средней доходности инвестиционного портфеля можно представить следующим образом:

, где (5.2.1)

n – число видов финансовых инструментов в портфеле;

r i – доходность i -го инструмента;

w i – доля (удельный вес) стоимости i -го инструмента в общей стоимости портфеля на начало периода.

Реальный срок вложения капитала может принимать любые значения – от одного дня до многих лет. Для обеспечения сопоставимости показателей доходности по инвестициям различной продолжительности эти показатели приводятся к единой временной базе – году (аннуилизируются). Методика аннуилизации доходности была рассмотрена в предыдущем параграфе. Однако, годовая доходность одних и тех же инвестиций может быть неодинаковой в различные промежутки времени. Например, доходность владения финансовым инструментом (за счет прироста его рыночной цены) составила за год 12%. В течение второго года цена увеличилась еще на 15%, а в течение третьего – на 10%. Возникает вопрос: чему равна средняя годовая доходность владения инструментом за 3 года? Так как годовая доходность суть процентная ставка, средняя доходность за период рассчитывается по формулам средних процентных ставок. В зависимости от вида процентной ставки (простая или сложная) ее средняя величина может определяться как среднеарифметическая, взвешенная по длительности периодов, в течение которых она оставалась неизменной, или как среднегеометрическая , взвешенная таким же образом (см. § 2.2).

В принципе возможно применение обоих способов для определения средней за несколько периодов доходности. Например, среднеарифметическая доходность инструмента, о котором говорилось выше, составит за три года 12,33% ((12 + 15 + 10) / 3). В данном случае продолжительность периодов, в течение которых доходность оставалась неизменной (год), не менялась, поэтому используется формула простой средней. Применив формулу средней геометрической, получим r ср = 12,315% (((1 + 0,12) * (1 + 0,15) * (1 + 0,1)) 1/3 -1). При незначительной разнице в результатах, техника вычисления среднеарифметической доходности значительно проще, чем среднегеометрической, поэтому довольно часто используется более простой способ расчета.

Однако при этом допускается существенная методическая ошибка : игнорируется цепной характер изменения доходности от периода к периоду. Доходность 12% была рассчитана к объему инвестиций на начало первого года, а доходность 15% — к их величине на начало следующего года. Эти величины не равны друг другу, так как в течение первого года инвестиции подорожали на 12%. За второй год они стали дороже еще на 15%, то есть их объем на начало третьего года также отличался от двух предыдущих сумм. Применяя формулу средней арифметической, молчаливо предполагают, что объем инвестиций оставался неизменным в течение всех периодов, то есть по сути рассчитывается средний базисный темп прироста. В данном случае это предположение совершенно неверно, поэтому следует рассчитывать средний цепной темп прироста по формуле средней геометрической, так как начальная сумма инвестиций меняется от периода к периоду. Представим исходные данные примера в табличной форме (табл. 5.2.1).

Таблица 5.2.1
Динамика доходности акции за 3 года
руб.

Источник

Основные методы анализа инвестиционных проектов

Методы оценки эффективности проектов – это способы определения целесообразности долгосрочного вложения капитала в различные объекты (проекты, мероприятия) с целью оценки перспектив их прибыльности и окупаемости.

Для оценки инвестиционного проекта можно использовать несколько основных методов анализа инвестиционных проектов это:

Методы оценки, используемые в отечественной практике (коэффициент эффективности – отношение среднегодовой суммы прибыли к сумме капитальных вложений и срок окупаемости – обратный ему показатель) имеют ряд существенных недостатков, которые не позволяют получить объективную оценку эффективности инвестиций:

При расчетах каждого из перечисленных показателей не учитывается фактор времени – ни прибыль, ни объем инвестиций не приводятся к настоящей стоимости. Тогда, в процессе расчета сопоставляются заведомо несопоставимые значения – сумма инвестиций в настоящей стоимости и сумма прибыли в будущей стоимости.

Показателем возврата инвестируемого капитала применяется только прибыль. Однако в реальной практике инвестиции возвращаются в виде денежного потока, состоящего из суммы чистой прибыли и аммортизации. Следовательно, оценка эффективности инвестиций только на основе прибыли сильно искажает результаты расчетов (искусственно занижает коэффициент эффективности и завышает срок окупаемости).

Рассматриваемые показатели позволяют получить только одностороннюю оценку эффективности инвестиционного проекта, так как оба они основаны на использовании одинаковых исходных данных суммы прибыли и суммы инвестиций).

Именно поэтому в мировой практике поток доходов от инвестиционного проекта корректируется с учетом фактора времени и уже в приведенном виде используется для расчета показателей.

Метод простой (бухгалтерской) нормы прибыли

Этот метод базируется на расчете отношения средней за период жизни проекта чистой бухгалтерской прибыли и средней величины инвестиций (затраты основных и оборотных средств) в проект. Выбирается проект с наибольшей средней бухгалтерской нормой прибыли.

Основным достоинством этого метода является его простота для понимания, доступность информации и несложность вычисления. Недостатком его нужно считать то, что он не учитывает не денежный (скрытый) характер некоторых видов затрат (к примеру амортизационные отчисления) и связанную с этим налоговую экономию, а также возможности реинвестирования получаемых доходов, времени притока и оттока денежных средств и временную стоимость денег.

Метод расчета периода окупаемости проекта

При использовании этого метода вычисляется количество лет, необходимых для полной компенсации первоначальных затрат, т.е. определяется момент, когда денежный поток доходов сравняется с суммой денежных потоков затрат. Проект с наименьшим сроком окупаемости выбирается.

Применяется также дисконтный метод окупаемости проекта – определяется срок, через который дисконтированные денежные потоки доходов сравняются с дисконтированными денежными потоками затрат. При этом используется концепция денежных потоков, учитывается возможность реинвестирования доходов и временная стоимость денег.

Обе модификации данного метода просты в понимании и применении и позволяют судить о ликвидности и рискованности проекта, поскольку длительная окупаемость означает длительную иммобилизацию средств (пониженную ликвидность проекта) и повышенную рискованность проекта.

Однако обе модификации игнорируют денежные поступления после истечения срока окупаемости проекта. Они успешно применяются для быстрой оценки проектов, а также в условиях значительной инфляции, политической нестабильности или при дефиците ликвидных средств – т.е. в обстоятельствах, ориентирующих организацию на получение максимальных доходов в кратчайшие сроки.

Метод чистой настоящей (текущей) стоимости (NPV)

Использование данного метода осложняется трудностью прогнозирования ставки дисконтирования (средней стоимости капитала) и/или ставки банковского процента.

Метод внутренней нормы рентабельности (IRR)

Все поступления и затраты по проекту приводятся к настоящей стоимости по ставке дисконтирования, полученной не на основе задаваемой извне средней стоимости капитала, а на основе внутренней ставки рентабельности самого проекта. Внутренняя ставка рентабельности определяется как ставка доходности, при которой настоящая стоимость поступлений равна настоящей стоимости затрат, т.е. чистая настоящая стоимость проекта равна нулю. Полученная таким образом чистая настоящая стоимость проекта сопоставляется с чистой настоящей стоимостью затрат. Одобряются проекты с внутренней нормой рентабельности, превышающей среднюю стоимость капитала (принимаемую за минимально допустимый уровень доходности).

Данный метод предполагает сложные вычисления и не всегда выделяет самый прибыльный проект. Метод предполагает мало реализуемую ситуацию реинвестирования всех промежуточных денежных поступлений от проекта по ставке внутренней доходности. Однако метод учитывает изменения стоимости денег во времени.

Следует отметить что, приведенные методы оценки инвестиционного проекта показывают, что в зависимости от того, какой критерий эффективности взят за основу для конкретного проекта, могут быть сделаны различные выводы. Поэтому при анализе инвестиционного проекта следует исходить из конкретных условий деятельности предприятия и поставленных при инвестировании целей. Как правило, наиболее объективную оценку дает комплексное применение различных методов оценки эффективности проектов.

Пример расчета показателей в Excel, используемых при анализе инвестиционного проекта рассмотрен в статье: Расчет показателей эффективности инвестиций

Источник

Метод средней доходности инвестиций

Метод средней доходности инвестиций (accounting rate of return) предполагает расчет по прогнозируемым потокам усредненного значения доходности вложенных средств и сравнения его с целевым коэффициентом доходности активов Целевой коэффициент доходности рассчитывается как доходность: 1) действующего производства корпорации, рассматривающей проект; 2) конкурирующей корпорации-аналога; 3) среднеотраслевая. Для адекватности сравнения рассчитывается показатель чистой прибыли по годам, а не чистого денежного потока.

Чем сильнее средняя доходность по проекту превышает сравнительные коэффициенты (по данной корпорации или среднеотраслевые данные), тем более привлекателен проект.

Правило средней доходности. Проект принимается, если его средняя доходность превышает целевую (сравниваемую) доходность.

Нашли применение два метода оценки средней доходности.

• Прогнозируемое значение чистой прибыли в году использования активов на полную проектную мощность относят к среднегодовой величине этих активов, т.е. доходность активов типичного года функционирования проекта сравнивается с целевыми коэффициентами.

• Предполагается нахождение усредненных значений прибыли и активов по всем годам функционирования проекта.

Для примера рассмотрим расчет средней доходности по проекту А, денежные потоки по которому приведены в табл. 7.1.

1. Пересчет чистых денежных потоков в показатель чистой прибыли:

Чистая прибыль за год = Чистый денежный поток соответствующего года — Амортизация за год = Усредненный чистый денежный поток — Годовая величина амортизации, исчисленная равномерным методом.

Амортизация в данном упрощенном примере может быть рассчитана как ежегодная величина износа. Суммарная величина амортизации за весь срок функционирования проекта должна покрыть величину активов. Предполагая, что все активы, для создания которых инвестируется 1000 млн. руб., амортизируются и метод начисления амортизации равномерный, годовая величина амортизации равна 1000/4 = 250. Общий чистый денежный поток за четыре года функционирования проекта составит 500 + 400 + 300 + 100 = 1300. Среднегодовое значение чистого денежного потока равно 1300/4 = 325. Среднее значение чистой прибыли составит 75 (325 — 250).

2. Расчет средней величины активов. По проекту А предполагается, что в году 0 будут приобретены активы на 1000 млн. руб. и к концу года 4 они полностью амортизируются. Средняя величина активов может быть рассчитана как (Активы на начало осуществления проекта + Активы на конец )/2. Активы на начало соответствуют величине инвестиционных затрат, а активы на конец — остаточной стоимости активов. В рассматриваемом примере остаточная стоимость равна нулю и средняя величина активов равна 500 х (1000 + 0)/2). Для всех случаев, когда амортизация равномерная и срок амортизации соответствует сроку функционирования проекта, средняя величина активов равна половине инвестиционных затрат. Если по проекту предполагается ликвидационная стоимость активов, то средняя величина активов равна (Инвестиционные затраты — Ликвидационная стоимость) / 2.

3. Расчет средней доходности, k = 75/500 = 15%. Если целевое значение доходности ниже 15%, то проект принимается.

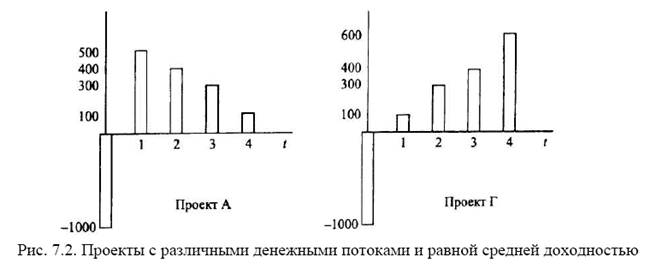
Метод средней доходности, так же как и метод срока окупаемости, не учитывает временную стоимость денег, т.е. различную оценку разновременных денежных потоков. Из-за этого средняя доходность не является истинной доходностью, получаемая оценка завышена. Зато в отличие от метода срока окупаемости в данном методе учитываются все денежные потоки по годам, а не только до срока окупаемости. Вследствие этого отличия методы могут давать прямо противоположные результаты. Сравним проекты А и Г (рис. 7.2) с одинаковым сроком функционирования, но различным характером денежного потока.

Срок окупаемости проекта А — 2,33 года, а проекта Г — 3,33 года. Однако при тех же предпосылках о величине активов и их амортизации средняя доходность по проекту Г выше (20%), и с точки зрения метода средней доходности проект Г предпочтительнее.

Достоинствами данного метода являются его простота, возможность сравнения проектов с разными объемами инвестиций и характером денежного потока.

К недостаткам относятся, во-первых, анализ по балансовому значению чистой прибыли, что не отражает величину реально доступных денежных средств, во-вторых, игнорирование временной стоимости денег.

Источник