Учетная норма прибыли (ARR)
Учетная норма прибыли (ARR) – это процентная норма прибыли, ожидаемая от инвестиций или активов по сравнению с первоначальной стоимостью вложений. ARR соотносит среднюю выручку от актива с суммой первоначальных инвестиций компании, чтобы получить в итоге коэффициент или прибыльность, которые можно ожидать в течение срока службы актива или связанного с ним проекта. ARR не учитывает временной стоимости денег или денежных потоков.
Формула ARR
Данный показатель вычисляется по следующей формуле:
Как рассчитать учетную норму прибыли:
- Рассчитайте годовую чистую прибыль от инвестиций, которая может включать выручку за вычетом любых ежегодных затрат или расходов на реализацию проекта или инвестиции;
- Если инвестиция представляет собой основной актив, такой как основные средства, вычтите любые расходы на амортизацию из годового дохода для получения годовой чистой прибыли.
- Разделите годовую чистую прибыль на первоначальную стоимость актива или инвестиции.
- Результат вычисления даст десятичную дробь. Умножьте результат на 100, чтобы показать процент возврата в виде целого числа.
О чём говорит ARR
Учетная норма прибыли это своего рода метрика бюджетирования капитала, применяемая для быстрого расчета прибыльности инвестиций. ARR используется главным образом в качестве общего сравнения нескольких проектов между собой, для определения ожидаемой нормы прибыли от каждого из них.
ARR можно использовать при принятии решения об инвестициях или приобретении. Он учитывает любые возможные годовые расходы или амортизационные отчисления, связанные с проектом. Амортизация – это процесс учета, при котором стоимость основных средств распределяется или расходуется ежегодно в течение срока полезного использования актива.
Амортизация – это полезная учетная конвенция, которая позволяет компаниям не тратить всю стоимость крупной покупки в первый год, что позволяет компании получать прибыль от актива сразу же, даже в первый год его службы. При расчете ARR амортизационные расходы и любые ежегодные затраты должны вычитаться из годовой выручки, чтобы получить чистую годовую прибыль.
КЛЮЧЕВЫЕ МОМЕНТЫ
- ARR полезен при определении годовой процентной ставки доходности проекта;
- ARR может быть использован при рассмотрении нескольких проектов, поскольку он обеспечивает ожидаемый уровень отдачи от каждого из них;
- Тем не менее, ARR не делает различий между инвестициями, которые дают разные денежные потоки в течение всего срока реализации проекта.
Пример использования ARR
Рассматривается проект с первоначальными инвестициями в 250 000 долларов, и ожидается, что он будет приносить доход в течение следующих пяти лет. Ниже приведены подробности:
- первоначальные инвестиции: 250,000 $
- ожидаемый доход в год: $ 70,000
- сроки: 5 лет
- Расчет ARR: $70,000 (годовой доход) / $250,000 (первоначальная стоимость)
- ARR = .28 или 28% (.28 * 100)
Разница между ARR и RRR
Как уже говорилось, ARR – это годовая процентная прибыль от инвестиций, основанная на первоначальных затратах денежных средств. Ну а требуемая норма доходности (RRR), также известная как ставка барьера, является минимальной доходностью, которую инвестор принимает для инвестиций или проектов, в целях компенсации принимаемого на себя уровня риска.
RRR может варьироваться между инвесторами, потому что они имеют разную склонность к риску. Например, инвестор, не склонный к риску, скорее всего, потребует более высокой нормы прибыли от инвестиций, чтобы компенсировать любой риск с ними связанный. Важно использовать несколько финансовых показателей, включая ARR и RRR, при определении того, стоит ли инвестировать.
Ограничения использования ARR
ARR полезен при определении годовой процентной ставки доходности проекта. Однако расчет имеет свои ограничения.
ARR не учитывает временную ценность денег (TVM). Временная ценость (или временная стоимость) денег – это концепция, согласно которой деньги, доступные в настоящее время, стоят больше, чем идентичная сумма в будущем из-за своей потенциальной доходности. Другими словами, две инвестиции могут дать неравномерный годовой доход. Если один проект приносит больший доход в первые годы, а другой – в последующие, ARR не присваивает более высокую стоимость проекту, который приносит прибыль раньше (а ведь она может быть реинвестирована для получения большего количества денег в будущем).
Учетная норма доходности не учитывает повышенный риск проектов с достаточно большим сроком реализации и ту значительную неопределенность, которая связана с такого рода длительными периодами.
Кроме этого, ARR не учитывает влияние сроков денежных потоков. Скажем, инвестор рассматривает пятилетнюю инвестицию с первоначальными денежными затратами в размере 50 000 долларов, но инвестиции не приносят никакой прибыли до четвертого и пятого года. Инвестор должен быть в состоянии выдержать первые три года без какого-либо положительного денежного потока от проекта. Расчет ARR не будет учитывать отсутствие денежных потоков в первые три года.
Источник
Метод расчета коэффициента эффективности инвестиций (ARR –Accounting Rate of Return)
Этот метод имеет две характерные черты: он не предполагает дисконтирования показателей дохода; доход характеризуется показателем чистой прибыли PN (балансовая прибыль за вычетом отчислений в бюджет). Алгоритм расчета исключительно прост, что и предопределяет широкое использование этого показателя на практике: коэффициент эффективности инвестиций (ARR) рассчитывается делением среднегодовой прибыли (PN) на среднюю величину инвестиций. Коэффициент берется в процентах. Средняя величина инвестиций находится делением исходной суммы капитальных вложений на два (V/2), если предполагается, что по истечении срока реализации анализируемого проекта все капитальные затраты будут списаны. Если допускается наличие остаточной стоимости (RV), то ее оценка должна быть исключена [2, с.17-19].
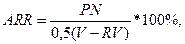 | (6) |
где PN — среднегодовая прибыль;
RV — остаточная стоимость.
Данный показатель сравнивается с показателем рентабельности авансированного капитала, рассчитываемого делением общей чистой прибыли предприятия на общую сумму средств, авансированных в его деятельность (итог среднего баланса нетто). Если сравниваются несколько альтернативных проектов, то предпочтение отдается тому, у которого коэффициент рентабельности авансированного капитала.
Недостатком данного метода является то, что он не учитывает времени притока и оттока средств, и доходы за более дальние года реализации проекта учитываются наравне с доходами полученными раньше.
При выборе эффективного проекта (эффективных проектов) производится сравнение значений показателей разных проектов, рассчитанных методами чистой текущей стоимости, внутренней нормы доходности, индекса прибыльности, периода окупаемости. Лучшим признается проект (проекты), имеющий оптимальные значения этих показателей по сравнению с другими либо с эталонными значениями подобных показателей.
Такой способ отбора является весьма логичным, поскольку позволяет в процессе выбора учесть особенности конкретного инвестиционного проекта. С точки зрения крупного инвестора предпочтителен критерий чистого дисконтированного дохода, показывающий массу получаемой от проекта чистой прибыли; средние и мелкие инвесторы заинтересованы в уменьшении времени оборота капитала, следовательно, для них весьма важен срок окупаемости инвестиций.
Тем не менее, выбор проекта по наилучшему значению какого-либо одного показателя экономической эффективности инвестиций не всегда корректен, так как не опирается на комплексную систему показателей эффективности инвестиций, вкладываемых в проект. На практике нередки ситуации когда, несмотря на высокие значения чистого дисконтированного дохода, внутренней нормы доходности и индексов доходности, проект не может быть принят из-за неудовлетворенного срока окупаемости инвестиций. Кроме того, выбор по наибольшему значению внутренней нормы доходности в ряде случаев может быть некорректен.
Рассмотрим использование этих методов на следующем примере.
Предприятие рассматривает возможность запуска опытного производства экологической продукции и её графического маркирования. Для этого необходимо 100 тыс. руб. на организацию производства. Выручка от реализации продукции прогнозируется по годам в следующих объемах: 1 год – 68000 руб.; 2 год – 74000 руб.; 3 год – 82000 руб.; 4 год – 80000 руб.; 5 год – 60000 руб.
Текущие расходы, включая расходы на рекламную компанию, оцениваются 34000 руб. в первый год с последующим ежегодным ростом их на 3%.
Цена авансированного капитала составляет 10 %.
Коэффициент рентабельности авансированного капитала 21- 22%.
Налог на прибыль составляет 24 %.
Руководство предприятия считает нецелесообразным участвовать в проектах со сроком более четырех лет.
Рассчитаем сначала чистые денежные поступления (см. таблицу 2).
Таблица 2 – Чистые денежные поступления (руб.)
| Годы |
| Объем реализации |
| Текущие денежные расходы |
| Износ по используемым основным фондам |
| Налогооблагаемая прибыль |
| Налог на прибыль |
| Чистая прибыль |
| Износ по используемым основным фондам |
| Чистые денежные поступления |
По формуле (1) получаем:
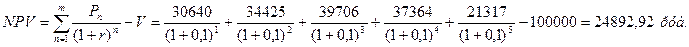 |
Так как, 24892,92 > 0, то проект следует принять
Рассчитаем теперь для нашего примера по формуле (2) индекс рентабельности инвестиций.
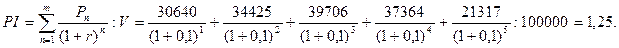 |
Проект следует принять, потому что 1,25>1.
Внутренняя норма доходности r для нашего проекта является корнем уравнения
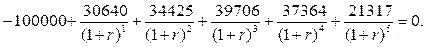 |
Для решения этого уравнения можно применить метод линейной интерполяции.
Однако проще рассчитать внутреннюю норму доходности инвестиций с помощью графического способа. Величина чистого приведенного эффекта зависит от ставки дисконтирования, то есть, NPV, как мы уже отмечали выше, есть функция r. Вычислим по формуле (1) значения NPV(r) инвестиционного проекта. Результаты вычислений представлены в таблице 3.
Таблица 3 – Значения NPV(r) инвестиционного проекта
| R (%) | NPV (руб.) |
| 28069,43 | |
| 24892,96 | |
| 21839,82 | |
| 18903,82 | |
| 16079,17 | |
| 13360,40 | |
| 10742,37 | |
| 8220,24 | |
| 5789,44 | |
| 3445,69 | |
| 1184,93 | |
| -996,68 | |
| -3102,74 | |
| -5136,67 | |
| -7101,69 | |
| -9997,76 | |
| -10837,08 | |
| -12613,07 | |
| -14331,43 | |
| -15994,61 | |
| -17604,95 | |
| -19164,66 |
При решении примера мы получили, что при NPV (19%) = 1184,93 руб., а NPV (20%) = — 996,68 руб.
Следовательно, в качестве начального приближения к корню уравнения можно использовать
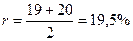 |
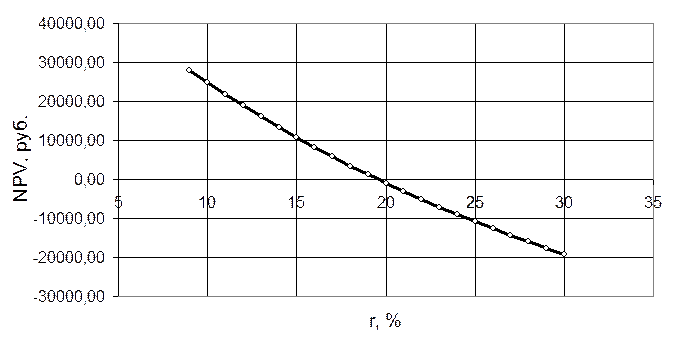
График функции NPV(r), построенный по найденным точкам, приведен на рисунке 1.
Из графика видно, что IRR = 19,54 %
Сравним внутреннюю норму доходности с ценой авансированного капитала, так как 19,54 % > 10 %. Значит, проект следует принять.
Если величина годовых денежных потоков по проекту неизменна, то вычисление внутренней нормы доходности можно осуществлять по следующей формуле:
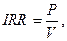 | (7) |
где Р – годовой поток денежных средств.
Предположим, например, что первоначальные инвестиции составили 20000 руб., а годовой поток равен 3254,90 руб. Подставив в формулу 7 эти данные получаем:
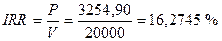 |
Подсчитаем число лет, в течение которых инвестиции будут полностью погашены накопляющимся доходом. К концу второго года окупятся 65065 руб. и останется 34935 руб., которые окупятся за часть третьего года, равную
34935/100000 = 0,35 года.
Период окупаемости инвестиционного проекта, таким образом, равен
2 + 0,35 = 2,35 года.
Среднегодовая балансовая прибыль за пятилетие равна:
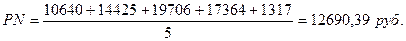 |
Рассчитаем, теперь, коэффициента эффективности инвестиций, по формуле (6)
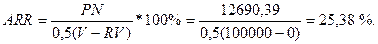 |
Как мы уже отмечали выше, данный коэффициент сравнивается с показателем рентабельности авансированного капитала. Проект принимается, потому что 25,38 % > 21-22 %.
Итоги оценки инвестиционного проекта представлены в таблице 4.
Таблица 4 – Результаты оценки проекта
| Метод расчета | Значение |
| Метод расчета чистого приведенного эффекта (NPV 10%) | 24892,96 руб. |
| Метод расчета индекса рентабельности инвестиций | 1,25 |
| Метод расчета внутренней нормы рентабельности инвестиций | 19,54 % |
| Метод определения срока окупаемости инвестиций | 2,35 года |
| Метод расчета коэффициента эффективности инвестиций | 25,38 % |
Как видно из таблицы 4, данный проект является эффективным по всем рассмотренным методам расчета привлекательности проекта.
Чистая приведенная стоимость и анализ безубыточности
Предположим, что предприятие рассматривает проект строительства новой линии, по которой
Проекты с различными сроками жизни.
Рассмотрим это на следующем примере. Есть два проекта «А» и «Б» с одинаковой суммой первоначальных вложений (см. таблицу).
| Год | Проект «А» | Проект «Б» |
| -100 | -100 | |
| NPV (r=15%) | 21,93 | 36,54 |
Как видно, из таблицы, проект «Б» является более выгодным, чем проект «А». Однако, так как срок реализации проектов не одинаков, необходимо использовать следующую формулу[1]:
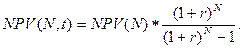 | () |
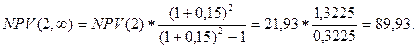 |
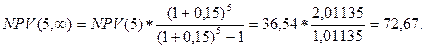 |
В результате вычислений следует, что надо отдать предпочтение проекту «А», так как он в большей степени увеличивает стоимость предприятия.
1. Бухвалов А. В., Бухвалова В. В., Идельсон А. В. Финансовые вычисления /Под общ. ред. А. В. Бухвалова. – СПб.: БХВ – Петербург, 2001. – 320 с.
2. Ефимова О. В. Финансовый анализ.-М.: Бухгалтерский учет, 1999.-320 с.
3. Ковалев В. В. Финансовый анализ.- М.: Финансы и статистика, 1996.–432 с.
4. Мазур И. И., Шапиро В. Д., Ольдегоре Н. Г. Управление проектами: Учебн. пособие для вузов. – М.: Экономика, 2001.- 574 с.
5. Серов В. М. Инвестиционный менеджмент. Учебн. пособие. – М.:ИНФРА-М, 2000. – 272 с.
6. Федько В.П., Альбеков А.У. Маркировка и сертификация товаров и услуг. — Ростов – на – Дону.: Фенинкс, 1998 г. – 639 с.
7. Хорн Дж. К. Ван. Основы управления финансами. – М.: Финансы и статистика, 1996. – 800 с.
8. Ченг Ф. Ли, Джозеф И. Финнерти. Финансы корпораций: теория, методы и практика. Пер. с англ. – М.:ИНФРА –М, 2000. –686 с.
[1] Ченг Ф. Ли, Джозеф И. Финнерти. Финансы корпораций: теория, методы и практика. Пер. с англ. – М.:ИНФРА –М, 2000. –с.132
Источник

