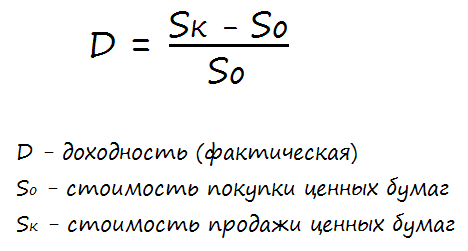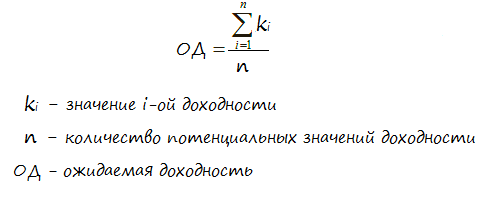Метод оценки по ожидаемой доходности

Способы оценки акций. Оценка акций по ожидаемой доходности и на базе роста дивидендов.

Любой инвестор для принятия решения о целесообразности приобретения акций компании должен обладать информацией о цене акций.

На практике применяют следующие методы расчета стоимости:

Оценка акций по ожидаемой доходности.

Метод базируется на основании оценки дохода в будущем, который инвестор будет иметь от владения ценными бумагами. В состав дохода входят два компонента — это дивиденд и прирост курсовой стоимости.

Оценка составляющих компонентов выполняется инвестором на основании анализа выплаты дивидендов в предшествующий период, динамики курсовой стоимости, прогнозирования развития фирмы. Инвестор должен сопоставить ожидаемый доход с необходимой доходностью. За необходимую доходность принимают доходность, желаемую для получения на вложенный капитал. Необходимая доходность состоит из прибыли по безрисковым вложениям, премии за риск. В качестве параметра по безрисковым вложениям принимают доходность по ценным бумагам государства, риск по которым минимален.

Не смотря на высокий доход от вложения в ценные бумаги, инвестиции в ценные бумаги являются рискованными. Вложения в рискованные бумаги компенсируются инвестору премией (повышенной доходностью). Статистический анализ за длительный временной период дает возможность оценить величину премии по разным видам ЦБ. Инвестирование в обыкновенные акции предприятий (рискованные активы) определяет получение более высокой доходности, чем по ценным бумагам государства.

Для определения уровня риска и значения премиальных, инвестору необходимо знать инвестиционные свойства акций. Это возможно сделать с помощью информационных агентств, публикующих рейтинг бумаг. В зарубежной практике обыкновенные акции классифицируют по эффективности деятельности на группы А и В. Акции группы А имеют меньшую доходность, чем акции группы В. Инвестор, поняв к какой группе относятся акции, имеет возможность установить премию за риск, доходность.

Оценка на базе роста дивидендов.

Инвесторы используют оценку имущества в виде оценки акций, используя модель роста (постоянного) дивидендов. Использование модели предполагает следующие допущения:

• темп увеличения дивидендных выплат ежегодно одинаков;
• темп увеличения дивидендов соответствует темпу роста активов предприятия;
• необходимая доходность выше темпа роста выплат по дивидендам.

Недостаток модели состоит в том, что рост дивидендных выплат реально не всегда соответствует росту компании, а также изменению цен на рынке. Часто предприятия создают видимость успешной деятельности, выплачивают дивиденды за счет уменьшения прибыли, идущей на развитие производства. При этом в целом темп роста предприятия замедляется. Возможна противоположная ситуация, когда собрание акционеров решает не выплачивать дивиденд, чистую прибыль направить на увеличение активов. Инвестор в такой ситуации не заинтересован, поскольку отсутствует текущий доход, акции обесценены. Но такое мнение инвестора может быть ошибочным в силу увеличения стоимости компании, величины активов, приходящихся на одну акцию, дохода в будущем.

Модифицированная модель оценки учитывает реинвестирование части прибыли с конкретным уровнем доходности.

Таким образом, с точки зрения инвестора существуют методы оценки пакета ценных бумаг для принятия решения о приобретении ценных бумаг. Профессионально процесс определения стоимости ценных бумаг выполняют эксперты оценочных компаний.

ООО «Премьер-Оценка», 2018. Тел.: +7 (495) 646-03-84; +7 (905) 740-67-75

Источник

Доходность ценных бумаг. Основные методы оценки и прогнозирования

Ни для кого не секрет, что основной целью инвестиций в ценные бумаги является получение максимально возможной прибыли при сохранении приемлемого уровня риска. В этой статье я расскажу вам о том, какие виды ценных бумаг обладают потенциально большим потенциалом доходности. Вы узнаете о том из чего складывается их доходность и каким образом она вычисляется. Наконец, мы с вами подробно поговорим о том, как можно провести предварительную оценку и рассчитать ожидаемую доходность ценных бумаг ещё на этапе их выбора.

Какие бумаги потенциально самые прибыльные

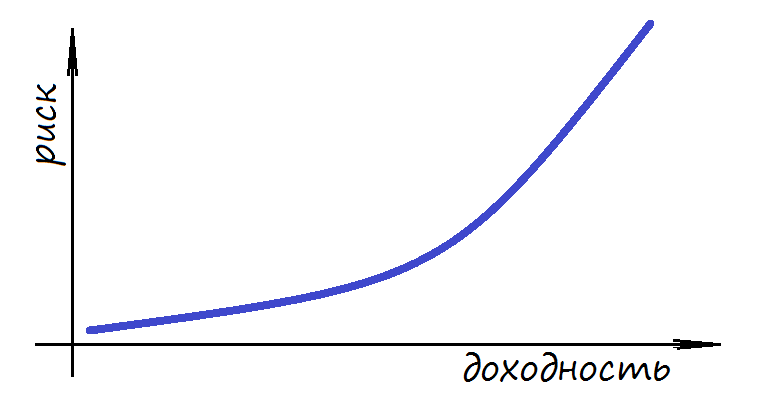
Ответ на этот вопрос довольно прост: самый большой потенциал в плане прибыли имеют ценные бумаги с таким же большим уровнем риска. Чем выше риск, который готов взять на себя инвестор, тем выше тот доход, который он может в итоге получить. Ключевое слово в данном случае – «может», поскольку с увеличением степени риска вероятность получения дохода постепенно тает.

Соотношение риска и доходности

То есть, другими словами, увеличивая степень риска инвестор одновременно и повышает свою потенциальную доходность, и снижает вероятность её получения. Поэтому в инвестициях так важно найти ту самую золотую середину, тот уровень риска при котором можно рассчитывать на относительно высокую прибыль с достаточно большой вероятностью её получения.

Минимальным риском, но и наименьшей степенью доходности отличаются такие бумаги, как государственные облигации. Обычно процент по ним сопоставим с доходностью банковских депозитов и едва превышает текущий уровень инфляции. Инвестирование в бумаги данного типа целесообразно в тех случаях, когда основной целью является не приумножение, а сохранение своих денежных средств.

На ступеньку выше стоят корпоративные облигации крупнейших компаний. Они также обладают достаточной степенью надёжности, но позволяют получить чуть большую прибыль (в отличие от бумаг выпущенных государством). Ещё выше по доходности – акции тех же самых компаний, но и риск по ним тоже чуть выше. Облигация по природе своей — долговая ценная бумага, то есть она подразумевает возврат долга и процентов по нему в любом случае. А вот акция — бумага долевая. Она даёт своему владельцу долю в бизнесе компании её выпустившей, но вместе с этим он принимает на себя и определённые риски (в частности, убытки в результате возможного снижения курса акций).

Ещё более рисковыми, но и потенциально более доходными являются акции и облигации выпущенные не столь известными и не столь крупными компаниями. При этом, чем менее известна компания, тем большую прибыль она вынуждена обещать по своим облигациям (иначе никто не захочет их покупать) и тем сильнее могут в итоге «выстрелить» её акции. Ведь согласитесь, что у автосервиса за углом вашего дома, потенциал к возможному росту куда выше чем, например, у Газпрома или Сбербанка. Автосервис может увеличиться в тысячи раз развивая свой бизнес в сеть по всему городу, по всей стране или, в конце концов, даже по всему миру (вовсе не обязательно что он это сделает, но, тем не менее, теоретическая возможность этого ведь существует). А вот Газпром это уже и так достаточно крупная организация и вряд ли он сможет увеличить свою рыночную капитализацию даже в 5-10 раз.

Есть ещё такие бумаги как фьючерсные и опционные контракты. Торговля ими осуществляется с использованием кредитного плеча (левериджа) и, соответственно, размер потенциальной прибыли в данном случае гораздо выше, он прямо пропорционален размеру предоставляемого плеча. Аналогичным образом растёт и риск.

Предположим, что вы решили приобрести фьючерс на акции IBM. Спецификация данного фьючерсного контракта подразумевает его торговлю с размером левериджа 1 к 10. То есть, при цене одной акции в 135 долларов, обладая суммой в 1350$, вы можете приобрести не десять, а сто таких акций. Хотя если говорить точнее, в данном случае вы приобретёте не сами акции IBM, а фьючерсный контракт на их покупку. Но сути дела это сильно не меняет, ведь по истечении срока данного контракта вы сможете получить прибыль равнозначную той, которая была бы у вас при продаже этих самых акций. Правда при этом и возможный убыток будет равен тому, который вам принесло бы обладание 100 акциями IBM в случае снижения их курсовой стоимости.

Формулы расчёта доходности ценных бумаг

Вообще, доходность по ценным бумагам может складываться из следующих величин:

1. Спекулятивный доход получаемый в результате реализации курсовой разницы при покупке и продаже ценных бумаг;
2. Доход получаемый в виде дивидендов по акциям или в виде процентов по облигациям (купонный доход).

Кроме этого можно говорить о фактической и ожидаемой доходности инвестиций. Фактическая доходность отражает ту величину прибыли, которая была получена, что называется, постфактум. А ожидаемая — показывает ту её величину, которую можно будет получить в будущем.

Про ожидаемую доходность мы поговорим в следующем разделе, а сейчас давайте рассмотрим как рассчитывается фактическая доходность инвестиций в ценные бумаги.

Если речь идёт о чисто спекулятивной доходности (от разницы курсовой стоимости), то её легко можно рассчитать по формуле:

В том случае, если помимо курсовой разницы были получены ещё проценты или дивиденды, доход рассчитывается по формуле:

Обычно доходность рассчитывается в процентах годовых. Для того чтобы привести рассчитанные по вышеприведённым формулам результаты к годовой доходности, следует воспользоваться этой зависимостью:

Ожидаемая доходность ценных бумаг

Грамотное инвестирование в ценные бумаги, предполагает вероятностную оценку рисков и возможностей, выбор допускаемого значения риска и сопоставимого с ним потенциального уровня доходности**. Об инвестиционных рисках и о способах их минимизации мы говорили с вами здесь. А сейчас я расскажу вам о том, как оценить потенциальную доходность ценных бумаг.

Оценить ожидаемую доходность (ОД) можно двумя различными методами. Первый метод основан на вероятностях (математическом ожидании), а второй — на исторических данных. Давайте начнём с вероятностного метода оценки.

** Как мы уже говорили с вами выше, риск и доходность ценных бумаг находятся в прямо пропорциональной зависимости друг от друга. Чем выше риск, тем выше потенциальный уровень доходности и наоборот. Такое положение вещей обусловлено тем, что рынок сам устанавливает данное соотношение, ведь никто не хочет покупать высокорисковые бумаги с небольшим уровнем доходности.

Оценка доходности на основе математического ожидания

В данном случае учитываются все возможные варианты размера предполагаемой доходности вкупе с их вероятностью. Причём наибольший вес придаётся тем значениям, вероятность получения которых выше.

Расчёт производится по формуле:

Для наглядности вычислений, давайте приведём простой пример. Допустим перед инвестором встал выбор из двух бумаг со следующим распределением вероятностей прибылей по ним:

1. Бумага А предположительно принесёт доходность в 10% с вероятностью в 50%, доходность в 7% с вероятностью в 30% или доходность в 4% с вероятностью в 20%;
2. Бумага Б. Вероятность доходности в 12% составляет 30%, вероятность доходности в 8% составляет 35% и вероятность доходности в 5% составляет 35%.

Сначала рассчитываем ожидаемую доходность для бумаги А:

ОД = (0,1*0,5) + (0,07*0,3) + (0,04*0,2) = 0,079 = 7,9%

А теперь рассчитаем ожидаемую доходность для бумаги Б:

ОД = (0,12*0,3) + (0,08*0,35) + (0,05*0,35) = 0,081 = 8,1%

Очевидно, что фактическое значение доходности, скорее всего, будет несколько отличаться от рассчитанного по вышеприведённой формуле. Оценить разброс значений фактических, относительно значений расчётных, можно рассчитав величину дисперсии.

Дисперсия рассчитывается по формуле:

Для нашего примера получим дисперсию для бумаги А:

0,5(0,1 — 0,079) 2 + 0,3(0,07 — 0,079) 2 + 0,2(0,04 — 0,079) 2 = 0,000549

И дисперсию для бумаги Б:

0,3(0,12 — 0,081) 2 + 0,35(0,08 — 0,081) 2 + 0,35(0,05 — 0,081) 2 = 0,000793

Дисперсия показывает тот уровень риска, который повлечёт за собой инвестирование в бумагу для которой была рассчитана ожидаемая доходность на основе вероятностей (математического ожидания). Чем больше дисперсия, тем больше возможное отклонение фактического значения ОД от расчётного.

В нашем примере дисперсия для бумаги Б несколько выше аналогичного показателя для бумаги А. Однако, разница между ними совсем незначительная (не на порядок), поэтому можно считать, что риски рассматриваемых бумаг примерно равны. Следовательно, при прочих равных, инвестирование в бумагу Б является предпочтительным.

Оценка доходности на основе исторических данных

Как вы понимаете, не всегда есть возможность объективно оценить вероятности получения того или иного размера прибыли. Поэтому, на практике часто используют второй метод оценки ОД. Для второго способа расчёта ОД предполагается наличие данных по доходности за несколько равных временных периодов (например, за несколько лет).

Расчёт производится по следующей формуле:

Для примера, давайте опять сравним акции двух компаний А и Б. Для простоты примера возьмём статистику годовой доходности за три последних года. Пускай акции компании А приносили доход в размере:

1. Первый год — 10%;
2. Второй год — 8%;
3. Трети год — 15%.

А акции компании Б:

1. Первый год — 5%;
2. Второй год — 15%;
3. Третий год — 10%.

Подставляя эти значения в формулу получим, для акций компании А:

Для акций компании Б:

Как видите, согласно расчёту, акции компании Б оказываются чуть более выгодными. Однако следует иметь ввиду, что значения доходности в прошлом, не гарантируют её в будущем. Так, в данном примере, на третий год произошло некоторое снижение прибыли. Это может быть вызвано как временными, но преодолимыми трудностями (вызванными, например, изменением конъюнктуры на рынках сбыта), так и свидетельствовать о более серьёзных проблемах компании (наличие которых, скорее всего, повлечёт за собой дальнейшее снижение прибыльности её бумаг).

Источник

CFA — Ожидаемая доходность, ковариация и корреляция активов инвестиционного портфеля

Расчет и интерпретация ожидаемой доходности, дисперсии доходности, ковариации и корреляции активов инвестиционного портфеля являются фундаментальными навыками финансового аналитика. Рассмотрим эти концепции, — в рамках изучения количественных методов по программе CFA.

Современная теория инвестиционного портфеля часто использует идею о том, что инвестиционные возможности можно оценить с использованием ожидаемой доходности в качестве меры вознаграждения и дисперсии доходности в качестве меры риска.

Расчет и интерпретация ожидаемой доходности и дисперсии доходности портфеля являются фундаментальными навыками финансового аналитика. В этом разделе мы рассмотрим концепции ожидаемой доходности портфеля и дисперсии доходности.

Хотя в этом разделе мы коснемся ряда основных понятий, мы не будем разбирать портфельную теорию как таковую. Портфельная теория Марковица (англ. ‘mean-variance analysis’) будет рассматриваться в следующих чтениях.

Доходность портфеля определяется доходностью отдельных его составляющих. В результате расчет дисперсии портфеля как функция доходности отдельного актива является более сложным, чем расчет дисперсии, проиллюстрированный в предыдущем разделе.

Рассмотрим пример портфеля,

• 50% которого инвестируются в фонд индекса S&P 500,
• 25% — в фонд долгосрочных корпоративных облигаций США, и
• 25% — в фонд индекса MSCI EAFE (представляющий рынки акций в Европе, Австралии и на Дальнем Востоке).

Таблица 5 показывает это распределение.

Таблица 5. Портфельные веса.

Долгосрочные корпоративные облигации США

Сначала рассмотрим расчет ожидаемой доходности портфеля. В предыдущем разделе мы определили ожидаемое значение случайной величины как средневзвешенную вероятность возможных результатов случайной величины.

Мы знаем, что доходность портфеля — это средневзвешенная доходность ценных бумаг в портфеле. Аналогично, ожидаемая доходность портфеля представляет собой средневзвешенную величину ожидаемой доходности ценных бумаг в портфеле с использованием точно таких же весов.

Когда мы оценили ожидаемую доходность отдельных ценных бумаг, мы сразу же получили ожидаемую доходность портфеля. Этот удобный факт вытекает из свойств ожидаемого значения.

Свойства ожидаемого значения.

Пусть \( w_i \) — любая постоянная величина (константа), а \( R_i \) — случайная величина.

1. Ожидаемое значение постоянной величины, умноженной на случайную величину, равно постоянной, умноженной на ожидаемое значение случайной величины.

2. Ожидаемое значение взвешенной суммы случайных величин равно взвешенной сумме ожидаемых значений с использованием тех же весов.

\( E (w_1R_1 + w_2R_2 + \ldots + w_nR_n) \)
\(= w_1E (R_1) + w_2E(R_2) + . + w_nE(R_n) \)
(формула 13)

Предположим, у нас есть случайная величина с заданным ожидаемым значением. Например, если мы умножим каждый результат на 2, ожидаемое значение случайной величины умножится также на 2. В этом смысл части 1.

Второе утверждение — это правило, которое напрямую приводит к выражению ожидаемой доходности портфеля.

Портфель с n ценными бумагами определяется весами его портфеля, \( w_1, w_2, \ldots, w_n \), которые в сумме составляют 1. Таким образом, доходность портфеля, \( R_p \), равна \( R_p = w_1R_1 + w_2R_2 + \ldots + w_nR_n \).

Теперь мы можем сформулировать следующий принцип:

Расчет ожидаемой доходности портфеля.

Для портфеля с n ценными бумагами ожидаемая доходность портфеля представляет собой средневзвешенную ожидаемую доходность по включенным в него ценным бумагам:

\( \begin E(R_p) &= E(w_1R_1 + w_2R_2 + \ldots + w_nR_n) \\ &= w_1E(R_1) + w_2E(R_2) + \ldots + w_nE (R_n) \end \)

Предположим, мы оценили ожидаемую доходность активов в портфеле, как показано в Таблице 6.

Таблица 6. Веса и ожидаемая доходность активов в портфеле.

Долгосрочные корпоративные облигации США

Мы рассчитываем ожидаемую доходность портфеля как 11.75%:

\( \begin E(R_p) &= w_1E(R_1) + w_2E(R_2) + w_3E (R_3) \\ &= 0.50(13\%) + 0.25(6\%) + 0.25(15\%) = 11.75\% \end \)

В предыдущем разделе мы изучали дисперсию как меру рассеивания результатов вокруг ожидаемого значения. Здесь нас интересует дисперсия доходности портфеля как мера инвестиционного риска.

Если \( R_p \) обозначает доходность портфеля, то дисперсия доходности портфеля составляет \( \sigma^2(R_p) = E \Big\ < \big[R_p - E(R_p)\big]^2 \Big\>\) в соответствии с Формулой 8.

Как можно использовать это определение на практике?

В чтении о статистических концепциях и рыночной доходности мы узнали, как рассчитать историческую или выборочную дисперсию на основе выборки ставок доходности.

Теперь мы рассматриваем дисперсию в прогностическом смысле. Мы будем использовать информацию об отдельных активах в портфеле, чтобы получить доходность всего портфеля.

Чтобы избежать беспорядка в обозначениях, мы пишем \( ER_p \) вместо \(E(R_p)\). Нам нужна концепция ковариации.

Определение ковариации.

Для двух случайных величин \(R_i\) и \(R_j\) ковариация между \(R_i\) и \(R_j\) равна

\( \textrm \big(R_i, R_j\big) = E \big[(R_i — ER_i) (R_j — ER_j)\big] \)

(Формула 14)

Альтернативными обозначениями являются \(\sigma(R_i,R_j)\) и \(\sigma_\).

Формула 14 утверждает, что ковариация (англ. ‘covariance’) между двумя случайными переменными является средневзвешенной вероятностью для перекрестных произведений отклонения каждой случайной переменной от ее собственного ожидаемого значения.

Используя определением дисперсии, мы находим:

\( \begin &= E \big[w_1w_1(R_1 — ER_1)(R_1 — ER_1) + w_1w_2(R_1 — ER_1)(R_2 — ER_2) \\ &+ w_1w_3(R_1 — ER_1)(R_3 — ER_3) + w_2w_1(R_2 — ER_2)(R_1 — ER_1) \\ &+ w_2w_2(R_2 — ER_2)(R_2 — ER_2) + w_2w_3(R_2 — ER_2)(R_3 — ER_3) \\ &+ w_3w_1(R_3 — ER_3)(R_1 — ER_1) + w_3w_2(R_3 — ER_3)(R_2 — ER_2) \\ &+ w_3w_3(R_3 — ER_3)(R_3 — ER_3) \big] \end \)
(выполняем умножение)

\( \begin &= w^1_2E \big[(R_1 — ER_1)^2 \big] + w_1w_2E \big[(R_1 — ER_1) (R_2 — ER_2) \big] \\ &+ w_1w_3E \big[(R_1 — ER_1) (R_3 — ER_3) \big] + w_2w_1E \big[(R_2 — ER_2) (R_1 — ER_1) \big] \\ &+ w^2_2E \big[(R_2 — ER_2)^2 \big] + w_2w_3E \big[(R_2 — ER_2) (R_3 — ER_3) \big] \\ &+ w_3w_1E \big[(R_3 — ER_3) (R_1 — ER_1) \big] + w_3w_2E \big[(R_3 — ER_3) (R_2 — ER_2) \big] \\ &+ w^2_3E \big[(R_3 — ER_3)^2 \big] \end \)

(напомим, что \(w_i\) являются постоянными величинами)

\( \begin &= w^2_1 \sigma^2 (R_1) + w_1w_2 \textrm (R_1, R_2) + w_1w_3 \textrm (R_1, R_3) \\ &+ w_1w_2 Cov(R_1, R_2) + w^2_2 \sigma^2 (R_2) + w_2w_3 \textrm (R_2, R_3) \\ &+ w_1w_3 Cov(R_1, R_3) + w_2w_3 Cov(R_2, R_3) + w^2_3 \sigma^2 (R_3) \end \)
(формула 15)

Последний шаг следует из определений дисперсии и ковариации.

Полезные факты о дисперсии и ковариации включают в себя следующее:

1. Дисперсия постоянной величины (константы) умноженная на случайную величину равна квадрату константы умноженной на дисперсию случайной величины, или \( \sigma^2(wR) = w^2\sigma^2(R) \);
2. Дисперсия константы плюс случайная величина равна дисперсии случайной величины, или \( \sigma^2(w + R) = \sigma 2(R)\), поскольку константа имеет нулевую дисперсию;
3. Ковариация между константой и случайной величиной равна нулю.

Для выделенных курсивом ковариационных членов в Формуле 15 мы использовали тот факт, что порядок переменных в ковариации не имеет значения: например, \(\textrm(R_2,R_1) = \textrm(R_1,R_2) \).

Как мы покажем далее, диагональные дисперсионные члены \(\sigma^2(R_1)\), \(\sigma^2(R2)\) и \(\sigma^2(R_3)\) могут быть выражены как \(\textrm(R_1,R_1)\), \(\textrm(R_2,R_2)\) и \(\textrm(R_3,R_3)\), соответственно.

Опираясь на этот факт, можно вывести наиболее компактный вид Формулы 15:

\( \sigma^2(R_p) = \sum_^ <3>\sum_^<3>w_i w_j \textrm(R_i,R_j) \)

Знаки суммирования говорят: «Установите i = 1, и пусть j меняется от 1 до 3; затем установите i = 2 и пусть j меняется от 1 до 3; затем установите i = 3 и пусть j меняется от 1 до 3; наконец, добавьте девять членов».

Эту формулу можно использовать для портфеля любого размера n:

\( \sigma^2(R_p) = \sum_^ <3>\sum_^<3>w_i w_j \textrm(R_i,R_j) \)
(Формула 16)

Из Формулы 15 видно, что отдельные отклонения доходности составляют часть, но не все отклонения портфеля. Три отклонения фактически превосходят по численности шесть ковариационных членов вне диагонали. Для трех активов это соотношение составляет 1 к 2 или 50 процентов.

Если имеется 20 активов, то есть 20 дисперсионных слагаемых и 20(20) — 20 = 380 недиагональных ковариационных слагаемых. Отношение слагаемых дисперсии к недиагональным слагаемым ковариации составляет менее 6 к 100, или 6%. Таким образом, первое наблюдение заключается в том, что с увеличением числа активов портфеля ковариация становится все более важной, в остальном все не меняется.

Когда значение ковариации как «недиагональной ковариации» очевидно, как здесь, мы опускаем уточняющие слова. Ковариация обычно используется в этом смысле.

Как именно влияет ковариация на дисперсию доходности портфеля?

Члены ковариации показывают, как совместное движение доходности отдельных активов влияет на дисперсию всего портфеля.

Например, рассмотрим две акции: одна имеет тенденцию к высокой доходности (относительно ее ожидаемой доходности), а другая имеет низкую доходность (относительно ее ожидаемой доходности).

Доходность одной акции имеет тенденцию компенсировать доходность другой акции, снижая изменчивость или дисперсию доходности портфеля.

Как и дисперсию, значения ковариации трудно интерпретировать, и мы вскоре представим более интуитивно понятную концепцию. Между тем, из определения ковариации мы можем установить два существенных примечания о ковариации.

1. Мы можем интерпретировать ковариацию следующим образом:

• Ковариация доходности отрицательна, когда доходность одного актива выше его ожидаемого значения, а доходность другого актива имеет тенденцию быть ниже его ожидаемого значения (средняя обратная зависимость между ставками доходности).
• Ковариация доходности равна 0, если доходность активов не связана.
• Ковариация доходности положительна, когда доходность обоих активов, как правило, находятся по одну сторону (выше или ниже) относительно ожидаемых значений в одно и то же время (средняя положительная зависимость между ставками доходности).

2. Ковариация случайной величины с самой собой (собственная ковариация) — это ее собственная дисперсия:

Полный список ковариаций составляет все статистические данные, необходимые для расчета дисперсии доходности портфеля. Ковариации часто представлены в табличном формате, который называется ковариационной матрицей (англ. ‘covariance matrix’).

В Таблице 7 показано, как вводятся расчетные значения в ковариационную матрицу для ожидаемой доходности и дисперсии доходности портфеля.

Таблица 7. Ожидаемая доходность и дисперсия портфеля — значения матрицы:

Для трех активов ковариационная матрица имеет \(3^2 = 3 \times 3 = 9 \) ячеек, но значения ячеек по диагонали (дисперсия) обычно рассчитываются отдельно от недиагональных ячеек. Эти диагональные значения выделены жирным шрифтом в Таблице 7.

Это различие естественно, так как дисперсия акций — это концепция с одной переменной. Таким образом, есть 9 — 3 = 6 ковариаций, исключая дисперсии.

Но \(\textrm(R_B,R_A) = \textrm(R_А,R_В)\), \( \textrm(R_С,R_A) = \textrm(R_B,R_A) \) и \( \textrm(R_С,R_B) = \textrm(R_B,R_C) \).

Ковариационная матрица под диагональю является зеркальным отображением ковариационной матрицы над диагональю. В результате, есть только 6/2 = 3 различных ковариационных члена для оценки. В целом, для n ценных бумаг существует \( n(n — 1)/2 \) различных ковариаций для оценки и n дисперсий для оценки.

Предположим, у нас есть ковариационная матрица, показанная в Таблице 8.

Мы будем работать с доходностью, указанной в процентах, а записи в таблице будут выражены в процентах в квадрате (% 2 ). Члены 38% 2 и 400% 2 равны 0.0038 и 0.0400 соответственно в десятичном виде; правильная работа в процентах и ​​десятичных дробях приводит к одинаковым ответам.

Таблица 8. Ковариационная матрица.

Долгосрочные корпоративные облигации США

Долгосрочные корпоративные облигации США

Если взять Формулу 15 и сгруппировать дисперсионные члены, мы получим следующее:

\( \begin \sigma^2(R_p) &= w_1^2 \sigma^2(R_2) + w_2^2 \sigma^2(R_2) + w_3^2 \sigma^2(R_3) + 2w_1w_2 \textrm(R_1,R_2) \\ &+ 2w_1w_3 \textrm(R_1,R_3) + 2w_2w_3 \textrm(R_2,R_3) \end \)
(Формула 17)

\( \begin &= (0.50)^2(400) + (0.25)^2(81) + (0.25)^2(441) \\ &+ 2(0.50)(0.25)(45) + 2(0.50)(0.25)(189) \\ &+ 2(0.25)(0.25)(38) \\ &= 100 + 5.0625 + 27.5625 + 11.25 + 47.25 + 4.75 = 195.875 \end \)

Разница составляет 195.875. Стандартное отклонение доходности составляет 195.875 1/2 = 14%. В итоге, ожидаемая годовая доходность портфеля составляет 11.75%, а стандартное отклонение доходности — 14%.

Давайте посмотрим на первые три члена в приведенном выше расчете. Их сумма, 100 + 5.0625 + 27.5625 = 132.625, является вкладом отдельных дисперсий активов в общую дисперсию портфеля. Если бы доходность по трем активам была независимой, ковариации были бы равны 0, а стандартное отклонение доходности портфеля составило бы 132.625 1/2 = 11.52% по сравнению с 14% ранее.

Портфель будет иметь меньший риск. Предположим, что члены ковариации были отрицательными. Тогда к 132.625 будет добавлено отрицательное число, поэтому дисперсия портфеля и риск будут еще меньше.

В то же время мы не изменили ожидаемую доходность. При той же ожидаемой доходности портфеля, портфель имеет меньший риск. Это снижение риска является преимуществом диверсификации, что означает снижение риска от владения портфелем активов.

Преимущество диверсификации увеличивается с уменьшением ковариации.

Это наблюдение является ключевым понятием современной теории портфеля. Это станет еще более интуитивно понятно, когда мы рассмотрим концепцию корреляции. Тогда мы сможем сказать, что до тех пор, пока ставки доходности акций портфеля не имеют абсолютно положительной корреляции, возможны преимущества диверсификации.

Кроме того, чем меньше корреляция между доходностью акций, тем выше стоимость отказа от диверсификации (с точки зрения упущенных выгод от снижения риска), при прочих равных условиях.

Определение корреляции.

Корреляция (англ. ‘correlation’) между двумя случайными величинами, \(R_i\) и \(R_j\), определяется как:

\( \rho(R_i,R_j) = \ <\mathrm(R_i, R_j) \over \sigma(R_i)\sigma(R_j)> \).

Альтернативными обозначениями корреляции являются \(\textrm(R_i,R_j) \) и \( \rho_\).

Ковариация часто представляется с использованием выражения:

\( \textrm(R_i, R_j) = \rho(R_i,R_j) \sigma(R_i)\sigma(R_j) \)

Деление, указанное в определении, делает корреляцию чистым числом (т.е. без единицы измерения) и устанавливает границы для ее наибольшего и наименьшего возможных значений.

Используя приведенное выше определение, мы можем сформулировать корреляционную матрицу только на основе данных из ковариационной матрицы. В Таблице 9 показана матрица корреляции.

Источник