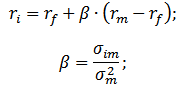Метод оценки доходности капитальных активов

Метод оценки капитальных активов (CAPM)

Модель оценки капитальных активов является одной из наиболее широко обсуждаемых разработок современной финансовой теории. Данная модель основывается на том факте, что инвесторы, вкладывающие свои средства в рисковые активы, ожидают некоторый дополнительный доход, превышающий безрисковую ставку, как компенсацию за риск владения этими активами. Технический термин, описывающий подобное требование, называется неприятием риска. Не принимающие риск инвесторы не обязательно избегают его, однако они требуют компенсации в форме дополнительного ожидаемого дохода за принятие риска по инвестициям, отдача по которым не гарантирована. Говоря проще, САРМ предполагает, что доход на рискованный актив является функцией некоторого безрискового дохода, плюс премия за риск, которая, в свою очередь, является функцией уровня риска, связанного с данным активом. Премия за риск рассчитывается как функция изменения цены данного актива за определенный период времени в сопоставлении с изменениями рынка в целом за тот же период. Таким образом, САРМ использует наиболее важную внешнюю переменную в оценке бизнеса, создавая теоретические рамки для определения соответствующей ожидаемой ставки дохода.

В соответствии с моделью оценки капитальных активов ставка дисконтирования находится по формуле:

R=Rf +b*(Rm- Rf),

v Rf — очищенная от риска ставка дохода;

b — коэффициент бета (является мерой систематического риска, связанного с макроэкономическими и политическими процессами, происходящими в стране);

v Rm — ставка дохода по среднерыночному портфелю ценных бумаг.

Данная модель является наиболее объективной (поскольку основана на реальной рыночной информации, а не на экспертной оценке) и широко используется в странах с развитыми рыночными отношениями.

Кроме того, для определения конечной ставки дисконтирования необходимо внести ряд поправок:

— корректировка на премию для малых предприятий, которая вносится ввиду того, что при расчете рыночной премии и коэффициента бета используются данные, полученные при изучении риска инвестирования в крупные компании, акции которых котируются на фондовых биржах;

— если при оценке компании обнаруживается, что ей присущ специфический риск, связанный с характером ее деятельности, то необходимо также добавить премию за риск, характерный для отдельной компании;

Таким образом, окончательный вид формулы для определения ставки дисконтирования скорректирован на дополнительные поправки и показан ниже:

R=Rf +b*(Rm- Rf)+S1+S2+C,

v S1 — премия для малых предприятий;

v S2 — премия за риск, характерный для отдельной компании;

v C — страновой риск.

Однако в рассматриваемом случае данный метод трудно применим по причине невозможности определения коэффициента b, поскольку он может быть рассчитан для компаний, акции которых котируются на фондовом рынке, а среднеотраслевой индекс, рассчитываемый аналитическими агентствами, не позволяет оценить степени риска конкретного предприятия. Коэффициент бета не будет отражать среднеотраслевых рисков.

Также определенные затруднения вызывает определение рыночной премии, ввиду нестабильности Российского фондового рынка.

Метод кумулятивного построения

Метод кумулятивного построения для определения ставки дисконтирования основан на экспертной оценке рисков, связанных с вложением средств в бизнес (реализуемый на базе оцениваемого имущественного комплекса). Ставка дисконтирования рассчитывается путем сложения всех выявленных рисков и прибавления полученного риска к безрисковой ставке дохода.

С учетом вышеизложенного, расчет ставки дисконтирования методом кумулятивного построения осуществляется на основании следующей формулы:

,

где	iД —	ставка дисконтирования, %;
iБР —	безрисковая составляющая ставки дисконтирования, %;
iР —	рисковая составляющая ставка дисконтирования, %.

,

Источник

Модель оценки капитальных активов | Capital Asset Pricing Model, CAPM

В финансах модель оценки капитальных активов (англ. Capital Asset Pricing Model, CAPM) применяется для определения требуемой нормы доходности актива или портфеля активов. Модель CAPM учитывает систематический (недиверсифицируемый) риск, мерой которого выступает бета-коэффициент, ожидаемую рыночную доходность и безрисковую процентную ставку.

Исходные положения модели CAMP

Большинство исходных положений модели строятся исходя из гипотезы эффективности рынка.

1. Все инвесторы действуют рационально и не склонны к риску, преследуя цель максимизации своего благосостояния на конец периода (предполагается, что инвестиционный горизонт у всех инвесторов одинаковый).
2. Рынки являются совершенными: модель оценки капитальных активов не учитывает транзакционные издержки, налоги, инфляцию и существующие ограничения на короткую продажу.
3. Все инвесторы могут получать или предоставлять неограниченное финансирование по безрисковой процентной ставке.
4. Все инвесторы имеют одинаковый доступ к информации, а среднеквадратическое отклонение доходности актива является единственным показателем меры риска. Следовательно, у всех инвесторов будут одинаковые ожидания относительно доходности определенного актива.
5. Все активы бесконечно дробиться и являются абсолютно ликвидными.
6. Общее количество активов на рынке является фиксированным в пределах определенного периода времени.
7. Распределение доходности активов является нормальным или близким к нормальному.
8. Все рынки находятся в равновесии, и ни один участник самостоятельно не может повлиять на цену актива.

Формула

Модель CAMP дает возможность рассчитать ожидаемую доходность определенной ценной бумаги, для чего необходимо воспользоваться следующей формулой:

где — ожидаемая норма доходности i-ой ценной бумаги.

K_RF – безрисковая процентная ставка;

β_i – бета-коэффициент i-ой ценной бумаги;

– ожидаемая доходность рыночного портфеля.

При этом премию за риск для рыночного портфеля (RP_p) можно рассчитать следующим образом:

В свою очередь, премия за риск для i-ой ценной бумаги (RP_i) составляет:

Пример расчета

Исторические данные о доходности акций Компании XYZ и доходности рыночного портфеля представлены в таблице:

При этом безрисковая процентная ставка составляет 1,5%.

Ожидаемая доходность рыночного портфеля составит 3,208%.

= (2,25+2,43+2,74+3,21+3,05+3,27+3,59+3,86+3,67+4,01)/10 = 3,208%

Бета-коэффициент акций Компании XYZ составит 1,74, что говорит об относительно высоком риске инвестирования в эти ценные бумаги. (О том, как рассчитывается бета-коэффициент можно прочитать здесь)

Таким образом, согласно модели CAMP ожидаемая норма доходности акций Компании XYZ составит 6,98%.

= 1,5+3,208(3,208-1,5) = 6,98%

Ограничения в применении модели оценки капитальных активов

Хотя модель CAMP является достаточно простой в применении, многие ее исходные положения полностью или частично не выполняются на реальных рынках.

1. Отсутствие транзакционных издержек. Все сделки на реальных рынках предполагают наличие транзакционных издержек, причем их уровень может существенно отличаться для различных участников рынка. Например, для крупных институциональных инвесторов они будут значительно ниже, чем для мелких частных инвесторов, за счет эффекта масштаба деятельности.
2. Нулевые ставки налогообложения. Современные системы налогообложения могут быть достаточно сложными, особенно в отношении финансовых инвестиций. Налог на прирост капитала, налог на дивиденды, отложенный налог могут иметь различные ставки, что будет стимулировать инвесторов формировать свои портфели таким образом, чтобы минимизировать затраты, связанные с выплатой налогов. Все это снижает эффективность инвестиций и оказывает существенное воздействие на ценообразование активов.
3. Однородные ожидания инвесторов. Такая ситуация возможна только при наличии абсолютно эффективного рынка, что не встречается на практике. Однако следует отметить, что некоторые рынки характеризуются высокой степенью эффективности.
4. Возможность инвестирования в безрисковые активы. Наличие безрисковых ценных бумаг является одним из базовых предположений модели оценки капитальных активов. Однако на практике даже инвестиции в трежерис предполагают принятие некоторых рисков, а именно: риск инфляции, валютный риск, риск реинвестирования.
5. Возможность привлечения дополнительного финансирования под безрисковую процентную ставку. Получая дополнительное финансирование под безрисковую процентную ставку инвесторы увеличивают долю рисковых активов в своих портфелях. Однако в реальной практике стоимость привлечения финансирования для мелких инвесторов, как правило выше, чем для крупных институциональных.
6. Бета-коэффициент является полной мерой риска. Модель САРМ предполагает, что единственной мерой риска является бета-коэффициент, который характеризует волатильность доходности ценной бумаги относительно волатильности доходности рыночного портфеля. Однако на практике существует множество других видов риска, которые оказывают существенное воздействие на ценообразование активов и выбор инвесторов: риск инфляции, риск ликвидности, риск реинвестирования.
7. Распределение доходности активов является нормальным или близким к нормальному. На практике распределение доходности активов является близким к нормальному в очень редких случаях, что также оказывает влияние на выбор инвесторов при формировании портфелей.

Источник

Модель оценки капитальных активов – CAPM (У. Шарпа) в Excel

Рассмотрим практические аспекты построения модели оценки капитальных активов CAPM с помощью Excel для отечественных акций ОАО “Газпром”.

Модель оценки капитальных активов (англ. Capital Assets Price Model, CAPM) – модель оценки (прогнозирования) будущей доходности актива для инвесторов. Подход оценки активов был теоретически разработана еще в 50-е годы Г.Марковицем, и окончательно сформирован в виде модели в 60-е годы У.Шарпом (1964), Дж. Трейнором (1962), Дж. Линтнером (1965), Ж. Мосином (1966).

Модель CAPM основывается на гипотезе эффективного рынка капитала (Efficient Market Hypothesis, EMH), созданной еще в начале 20-го века Л. Башелье и активно продвигаемую Ю.Фамой в 60-е годы. Данная гипотеза имеет ряд условий по способу распространению информации и действию инвесторов на эффективном рынке капитала:

• Информация свободно распространяется и доступно всем инвесторам, рынок имеет совершенную конкуренцию. Другими словами, отсутствуют инсайдеры, которые обладают большим преимуществом в принятии решений и получении сверхдоходности (выше среднерыночной).
• Любое изменение информации о компании сразу приводит к изменению стоимости ее активов (акций). Это исключает возможность использования любой активной стратегии инвестирования для получения сверхприбыли. Данная предпосылка исключает возможность арбитражных сделок, когда инвестор заранее имеет полезную информацию, тогда как цена на активы компании еще не изменилась.
• Инвесторы на эффективном рынке имеют долгосрочный горизонт вложения. Это исключает возникновение резких изменений цен на активы (акции) и кризисов.
• Активы имеют высокую ликвидность и абсолютно делимы.

Исходя из гипотезы эффективного рынка, У. Шарп сделал предположение, что на будущую доходность акции будут оказывать влияние только рыночные (системные) риски. Другими словами, будущую доходность акции будут определять общее настроение рынка. Поэтому, кстати, он и был сторонником пассивного инвестирования, когда инвестиционный портфель не пересматривается от получения новой информации. Следует отметить, что на эффективном рынке невозможно получить сверхприбыль. Это делает любое активное управление инвестициями (инвестиционным портфелем) не целесообразным и ставит под сомнение эффективность вложения в ПИФы. В результате, модель У. Шарпа имеет всего один фактор – рыночный риск (коэффициент бета). Анализируя данные постулаты эффективного рынка, можно заметить, что в современной экономике многие из них не выполняются. Модель CAPM в большей степени является теоретической моделью и может использоваться на практике в общем случае.

★ Excel таблица для формирования инвестиционного портфеля ценных бумаг (рассчитай портфель за 1 минуту) + оценка риска и доходности

★ Программа InvestRatio – расчет всех инвестиционных коэффициентов в Excel за 5 минут (расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR) + прогнозирование движения курса

Модель CAPM. Формула расчета

Формула оценки будущей доходности актива (акции) по модели CAPM имеет следующий аналитический вид:

r – ожидаемая доходность актива (акций);

r_f – доходность по безрисковому активу;

r_m – среднерыночная доходность;

β – коэффициент бета (мера рыночного риска), который отражает чувствительность изменения стоимости активов в зависимости от доходности рынка. Данный коэффициент иногда называют коэффициент Шарпа.

Модель представляет собой уравнение линейной регрессии и показывает линейную взаимосвязь между доходностью (r) и рыночным риском (β);

σ_im – стандартное отклонение изменения доходности акции от изменения доходности рынка;

σ 2 _m – дисперсия рыночной доходности.

Оценка стоимости бизнеса	Финансовый анализ по МСФО	Финансовый анализ по РСБУ
Расчет NPV, IRR в Excel	Оценка акций и облигаций

Расчет модели CAPM в Excel

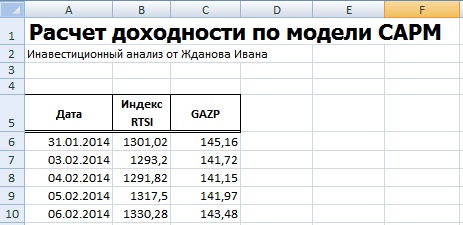
Для того чтобы лучше понять модель CAPM разберем ее на реальном примере акций предприятия ОАО «Газпром». Для этого воспользуемся программой Excel. Получить котировки акций можно на сайте finam.ru в разделе «Про рынок» ­→ «Экспорт данных».

В нашей формуле за рыночную доходность будем брать изменения индекса РТС (RTSI), также это может быть индекс ММВБ (MICECX). Для американских акций зачастую берут изменения индекса S&P500. Были взяты ежедневные котировки акции и индекса за 1 год (250 данных), начиная с 31.01.2014 по 30.01.2015 г.
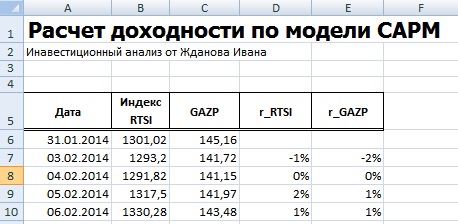
Далее необходимо рассчитать доходности акции (E) и индекса (D), по формулам:

Хочется заметить, что для оценки доходностей могла быть использована также формула расчета через натуральный логарифм:

Итоговый результат расчета доходности одинаковый.

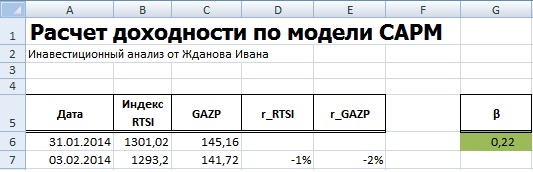
На следующем этапе необходимо рассчитать значение коэффициента бета, отражающего рыночный риск акции. Для этого есть два варианта расчета.

Расчет коэффициента бета с помощью формул Excel

Для расчета коэффициента бета можно воспользоваться формулой ИНДЕКС и ЛИНЕЙН, первая позволяет взять индекс b из формулы линейной регрессии между доходностями акции и индекса, который соответствует коэффициенту бета. Формула расчета будет следующая:

Расчет коэффициента бета через надстройку «Регрессия»

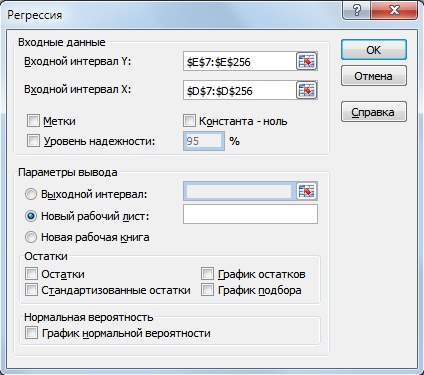
Второй вариант расчета рыночного риска модели заключается в использовании надстройки в разделе «Главное меню» → «Данные» →«Анализ данных» → «Регрессия».

В открывшемся окне необходимо заполнить два поля: «Входной интервал Y» и «Входной интервал Х» доходностями индекса и акции соответственно.

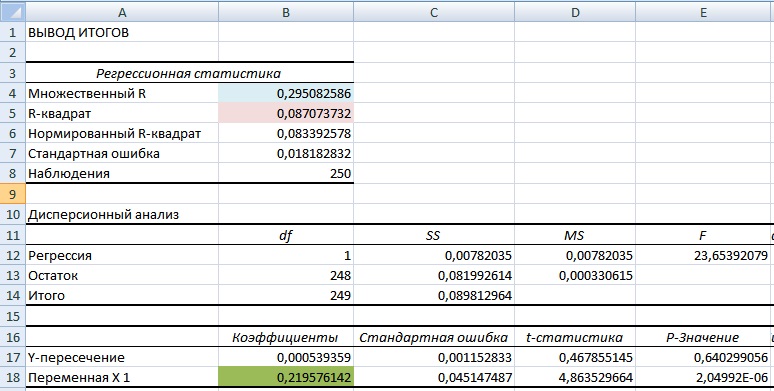
На новом листе Excel появится основные параметры модели линейной регрессии. В ячейке В18 отразится рассчитанный коэффициент линейной регрессии – коэффициент бета. Рассмотрим другие полученные параметры анализа. Так показатель Множественной R (коэффициента корреляции) между доходностью акции и индекса составляет 0,29, что показывает низкую степень зависимости доходности акции от доходности индекса. Коэффициент R-квадрат (коэффициент детерминированности) отражает точность полученной модели. Точность составляет 0,08, что очень мало для того чтобы принимать адекватные решения о прогнозировании будущей доходности на основе взаимосвязи только с уровнем риска рынка.

★ Программа InvestRatio – расчет всех инвестиционных коэффициентов в Excel за 5 минут (расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR) + прогнозирование движения курса

Что показывает коэффициент бета в модели CAPM?

Коэффициент бета показывает чувствительность изменения доходности акции и доходности рынка. Другими словами, отражает рискованность вложения в тот или иной актив. Коэффициент бета служит мерой рыночного риска. Знак перед показателем отражает их однонаправленное или разнонаправленное движение. Рассмотрим более подробно значение бета в таблице ниже:

Источник