Вероятностные методы анализа рисков
Имитационное моделирование по методу Монте-Карло (Monte-Carlo Simulation) позволяет построить математическую модель для проекта с неопределенными значениями параметров, и, зная вероятностные распределения параметров проекта, а также связь между изменениями параметров (корреляцию) получить распределение доходности проекта.
Блок-схема, представленная на рисунке отражает укрупненную схему работы с моделью.
Применение метода имитации Монте-Карло требует использования специальных математических пакетов (например, специализированного программного пакета Гарвардского университета под названием Risk-Master) , в то время, как метод сценариев может быть реализован даже при помощи обыкновенного калькулятора.
Как уже отмечалось, анализ рисков с использованием метода имитационного моделирования Монте-Карло представляет собой “воссоединение” методов анализа чувствительности и анализа сценариев на базе теории вероятностей.
Результатом такого комплексного анализа выступает распределение вероятностей возможных результатов проекта ( например, вероятность получения NPV 0, около 95%.
Будем исходить из того, что проект подлежит рассмотрению и считается выгодным, в случае, если NPV > 0. При сравнении нескольких одноцелевых проектов выбирается тот, у которого NPV больше при соблюдении сказанного в предыдущем предложении.
Источник
Метод монте карло расчет инвестиций
Статья продолжает вводный материал об имитационном моделировании методом Монте Карло (ММК). Рассмотрены базовые принципы оценки инвестиционных проектов через дисконтирование денежных потоков (DCF) и методом Монте Карло.
СОДЕРЖАНИЕ:
ВВЕДЕНИЕ.
В тексте о математическом моделировании, истории ММК и его простейших приложениях в математике, читатель имел возможность ознакомиться с сутью метода и с тем, насколько оригинально, с той или иной степенью точности, он позволяет решать задачи из школьного курса математики: вычислить число π и взять определенный интеграл.
Цель предлагаемой публикации – преимущества метода Монте Карло в инвестиционном анализе по сравнению с традиционным методом дисконтирования денежных потоков.
1. АНАЛИЗ ИНВЕСТИЦИОННОГО ПРОЕКТА МЕТОДОМ ДИСКОНТИРОВАНИЯ ДЕНЕЖНЫХ ПОТОКОВ
Общепризнанный критерий оценки инвестиционного проекта (ИП) – расчет чистой приведенной стоимости (ЧПС). Другое название – чистая современная стоимость, Net present value (NPV).
Математически NPV определяется методом дисконтирования денежных потоков, генерируемых данным ИП
Англоязычный термин – Discounted cash flow (DCF).
CFi, отвечающее инвестициям (вложениям, расходам) входит в формулу 1 со знаком «-», CFi, отображающие доход по проекту – со знаком «+». Значение i=0 (нулевой период) соответствует начальной инвестиции. В сумму она входит с отрицательным знаком и не дисконтируется (нулевая степень в знаменателе).
Инвестиционный проект признается успешным, если NPV>0.
Безусловно, выполнение этого неравенства является необходимым, но отнюдь не достаточным условием эффективности ИП.
Насколько NPV должно быть больше нуля? Естественно, чем оно выше, тем лучше. Из нескольких проектов, при прочих равных условиях, предпочтение отдадут ИП с максимальным NPV.
«Прочие условия» включают срок окупаемости, рентабельность и внутреннюю норму доходности [1] . Уменьшение срока окупаемости, повышение рентабельности и внутренней нормы доходности делает проект более привлекательным.
Но первое и главное условие жизнеспособности любого ИП – положительное значение чистой приведенной стоимости.
2. ИНВЕСТПРОЕКТ «МЕДПРЕПАРАТЫ». МЕТОД DCF
Рассчитаем чистую приведенную стоимость (NPV) условного примера вывода на рынок фармкомпанией некоего медицинского препарата.
(здесь и далее изложение построено на основе статьи [2] )
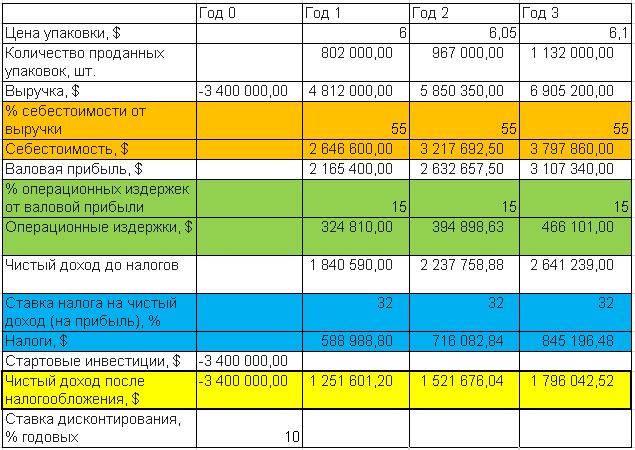
Ключевые показатели ИП представлены в следующей таблице:
Компания готова потратить на трехлетнюю программу $3,4 млн. Цена за упаковку предполагается по 6, 6,05 и 6,1 доллара в первый, второй и третий год соответственно. Количество проданных упаковок формирует итоговую выручку компании по годам. Фиксированными параметрами для ИП являются: процент себестоимости от выручки (55%), процент на операционные издержки от валовой прибыли (15%), ставка налога на прибыль (32%), ставка дисконтирования (средний уровень доходности на данном рынке инвестиций) – 10% годовых.
Читатель может самостоятельно вычислить NPV проекта по будущим потокам платежей (желтая строка в нижней части таблицы).
1) Подставить данные в формулу 1. Следует учесть, что начальная инвестиция в $3,4 млн входит в сумму со знаком минус и не дисконтируется. Об этой особенности определения NPV написано выше.
2) Воспользоваться функцией «ЧПС» из набора финансовых функций Excel. Во избежание недоразумений, в строку потоков для функции ЧПС надо вставить три положительных финпотока (первый, второй и третий годы) и из полученного результата вычесть $3,4 млн. Предполагается, что начальная инвестиция делается в конце «нулевого» года.
Очевидно, что правильно проведенные расчеты по обоим вариантам дадут одно и то же значение NPV=$344796>0.
Инвестиционный проект заслуживает внимания.
Excel позволяет легко рассчитать и такой важный показатель инвестанализа, как внутренняя норма (ставка) доходности (ВНД), Internal rate of return (IRR). Экономическая сущность IRR – ставка дисконтирования r, при которой чистая приведенная стоимость (NPV) равна нулю. IRR должна быть больше r, в противном случае, NPV будет отрицательным.
Для расчета IRR Excel предлагает функцию «ВСД», в строку значений которой заносятся числа из желтой строки Таблицы 1. IRR=15,33%>r (r=10% годовых). Другой путь, тоже в Excel – опция «Подбор параметра» по ставке дисконтирования для обнуления NPV.
3. МИНУСЫ МЕТОДА DCF
К сожалению, в общем случае, получение позитивной чистой приведенной стоимости на фиксированных входных данных, мало чем поможет финансовому аналитику. Динамика внешних рыночных (и не только) условий плохо предсказуема, а результаты инвестпроекта весьма к ним чувствительны.
Конкуренция способна привести к падению реализации и заставить менеджеров компании снижать отпускные цели. Плывут нормы себестоимости и операционных издержек. Что уж говорить о ставке дисконтирования r, которая чувствительна к различным финансово-экономическим воздействиям.
О проектах в подобной среде говорят, как об ИП с высоким уровнем непрерывной (рыночной) неопределенности.
Здесь классический метод дисконтирования денежных потоков (DCF) работает плохо.
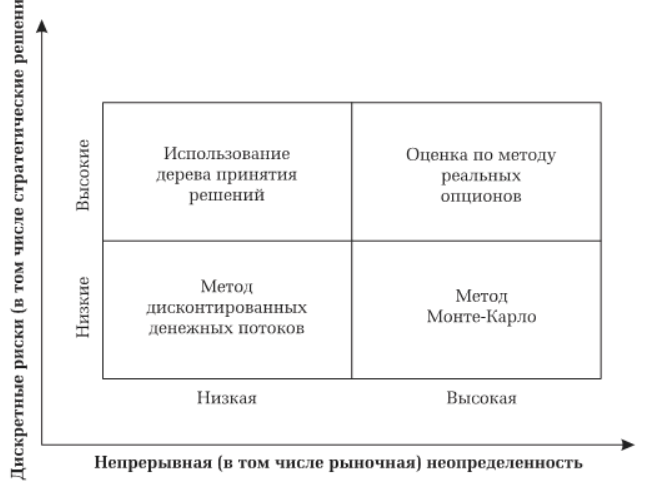
Вообще говоря, считается, что ИП подвержены двум глобальным видам риска. Дискретным (стратегическим) и уже упомянутым непрерывным (рыночным). Последние годы развития теории инвестиций предложили ряд альтернативных, относительно DCF, методик анализа ИП. Некоторые из них приведены ниже на диаграмме в координатах: дискретный риск – непрерывный риск.
(здесь и далее источник изображений или информации для построения таблиц – публикация [2] )
Видно, что метод дисконтированных денежных потоков расположен в наиболее комфортной зоне риска. Там, где его дискретный и непрерывный виды минимальны. Улучшить картинку на повышенных уровнях рыночных рисков позволяет метод Монте Карло (ММК).
4. ИНВЕСТПРОЕКТ «МЕДПРЕПАРАТЫ». МЕТОД МОНТЕ КАРЛО
Применим ММК к вероятностному моделированию ИП «Медпрепараты».
Напомним, что упрощенно суть имитационного метода Монте Карло заключается «в многократном повторении изучаемого процесса посредством генератора случайных чисел». На выходе имеем ключевые параметры проекта в виде вероятностных характеристик. Итог ММК – оценка их средних величин (матожиданий).
Главная мишень ММК для ИП «Медпрепараты» — цена препарата и объем продаж. Они, прежде всего, моделируются, как случайные величины.
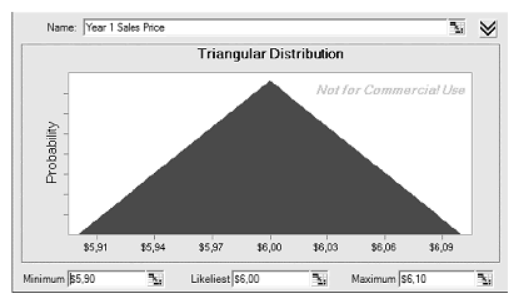
1) Цена препарата.
Для отпускных цен используется треугольное распределение:
«Треугольный» подход приемлем для обработки величин, которые поддаются известной степени контроля со стороны менеджеров проекта. Фигурируют минимальная (левый край треугольника), максимальная (правый рай) и наиболее вероятная цена (основание вершины треугольника).
Исходя из данных строки Таблицы 1 «Цена упаковки», для ММК формируется следующий «треугольный» массив:
Числа колонки «Цена2» Таблицы 2 повторяют значения строки «Цена упаковки» Таблицы 1. По всем годам имеет место равенство Цена2-Цена1=Цена3-Цена2. В итоге, на распределении получается симметричный, равнобедренный треугольник.
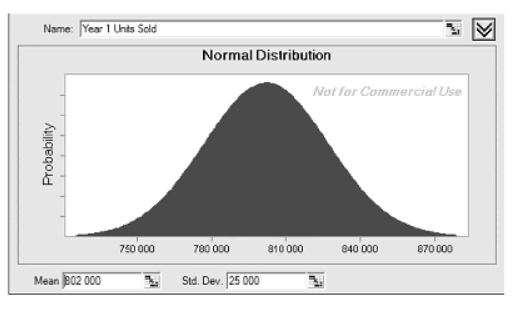
Предполагается, что у объема продаж нормальное распределение с определенным среднеквадратичным отклонением (СКО):
Для этой величины, отображенной в строке «Количество проданных упаковок» Таблицы 1, строится такая стартовая «вероятностная» таблица:
Вновь, проверим себя. Данные колонки 2 «Матожидание…» Таблицы 3 совпадают с содержанием строки «Количество проданных упаковок» Таблицы 1.
Себестоимость продукции (% от выручки) также задается треугольным распределением с параметрами (50%; 55%; 65%). По концам – максимум и минимум, в центре – наиболее вероятное значение в 55%, отображенное, как фиксированный показатель в Таблице 1. Аналитики полагают, что себестоимость будет скорее выше, чем ниже 55%. Получается треугольник с неравными сторонами, правая боковая сторона (бедро) больше левой.
Операционные затраты (% от валовой прибыли) представляются, как нормально распределенная случайная величина с матожиданием в 15% и СКО=2%.
Таким образом, почти все переменные инвестиционного проекта, имеющие ту или иную степень неопределенности, представлены, как случайные величины с вероятностными характеристиками. Постоянными для проведения данного анализа принимаются ставка дисконтирования (10% годовых) и налоговая нагрузка (32%).
Теперь все готово для запуска генератора случайных чисел для метода Монте Карло и последующей оценке NPV и IRR.
Исследователи провели 10 тысяч повторов, итераций.
Результаты для NPV и IRR сведены в следующие диаграммы:
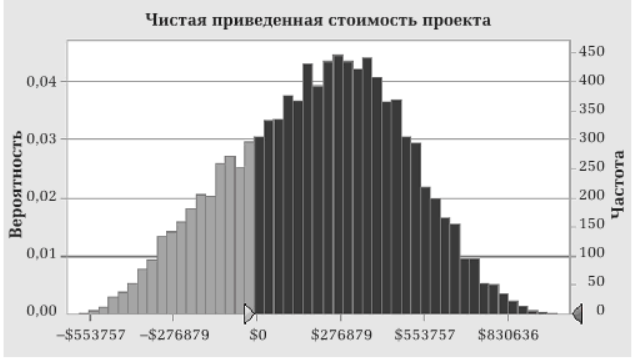
Распределение чистой приведенной стоимости (NPV)
Распределение внутренней ставки доходности (IRR)
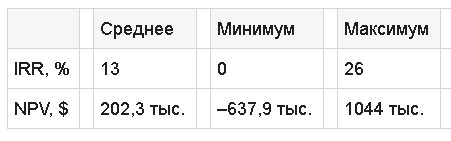
Анализ графиков позволяет построить таблицу минимальных, средних и максимальных значений для IRR и NPV:
Интересно, что среднее значение NPV ($202,3 тыс.) от ММК существенно меньше числа, полученного методом дисконтирования денежных потоков ($344,8 тыс.). На целых 41,3%. Определяющий вклад в такой разрыв внесло скошенное в большую сторону треугольное распределение себестоимости, см. выше.
Более того, согласно ММК, существует значительная вероятность того, что NPV уйдет в минус – 25% от общего количества сценариев. До (-$637,9 тыс.). С другой стороны, на правом конце гистограммы для NPV лежат отличные показатели эффективности ИП, с чистой приведенной стоимостью, вплоть до $1 млн. и выше.
Для внутренней нормы доходности диапазон значений простирается от нуля для отрицательных NPV и достигает, при самых благоприятных условиях, 26% годовых. Среднее значение в 13% годовых не слишком (на 15%) отличается от IRR по DCF в 15,33% годовых.
Очевидно, что метод Монте Карло гораздо более гибок, эффективен и полезен для анализа инвестиционных проектов с высоким уровнем непрерывного (рыночного) риска, по сравнению с методом дисконтирования денежных потоков. Последний может выполнять роль предварительной оценки ИП, некоего ориентира при отработке проекта посредством ММК.
ПРИМЕЧАНИЯ И ССЫЛКИ
- ↑ «Инвестиционный анализ», В.М. Аньшин, «Дело», Москва, 2000
- ↑ «Метод Монте Карло для финансовых аналитиков: краткий путеводитель», А.
ИСПОЛЬЗУЕМЫЕ СОКРАЩЕНИЯ
ММК – метод Монте Карло
ИП – инвестиционный проект
NPV – Net present value, чистая приведенная (современная) стоимость (ЧПС)
DCF – Discounted cash flow, метод дисконтирования денежных потоков
IRR – Internal rate of return, внутренняя ставка (норма) доходности (ВНД)
СКО – среднеквадратичное (среднеквадратическое, стандартное) отклонение, σ
Источник
Анализ методом Монте-Карло
Открыть эту статью в PDF
Монте-Карло — метод анализа, применяемый в случаях, когда параметры известны приблизительно, и есть информация о статистическом распределении этих параметров. Для проведения анализа генерируют большое число случайных значений параметров, для каждого такого значения выполняют расчет и формируют статистическое распределение для результата.
Примерами задач, для которых применяют анализ Монте-Карло, могут служить следующие ситуации :
- Оценка опционов на акции на основе статистических данных о колебаниях цены акции.
- Определение Value-at-Risk в инвестиционных решениях с известными данными о статистическом распределении доходности ценной бумаги.
- Оценка инвестиционных проектов, связанных с добычей полезных ископаемых или другой деятельностью, в которой данные о параметрах проекта (дебит нефтяной скважины и т. п.) выражены статистически.
Пример графика распределения значений NPV инвестиционного проекта методом Монте-Карло:
На этом графике по горизонтальной оси показан интервал значений NPV, полученных в расчетах (результаты сгруппированы с шагом 100 000), а по вертикальной оси — число случаев, когда NPV попадала в этот интервал (из 1 000 попыток).
Алгоритм метода Монте-Карло
В сфере финансов для анализа методом Монте-Карло необходимо выполнить следующие шаги:
Шаг 1. Параметры
Выбираем результат, который будем анализировать методом Монте-Карло — цена опциона, NPV инвестиционного проекта и т. п.
В качестве параметров для Монте-Карло выбираем один или несколько показателей, влияющих на результат . Предполагается, что значения этих параметров известны не точно, но мы знаем или можем получить характеристики статистического распределения параметров.
Шаг 2. Основная модель
Создаем модель, которая вычисляет результат с учетом выбранных параметров. Скорее всего, кроме статистических параметров, используемых в Монте-Карло, в ней будут и другие данные, которые заданы в традиционном виде с конкретными значениями. В финансовом анализе модель обычно создают в Excel, но, в принципе, метод Монте-Карло можно реализовать и другими инструментами : на языке Python или еще в каком-то приложении.
Шаг 3. Закон распределения
Необходимо решить, как именно выглядит статистическое распределение параметров. Простейший вариант — равномерное распределение. В этом случае параметр с одинаковой вероятностью может принимать любое из значений в заданном интервале. К сожалению, такое распределение случайных величин не очень часто соответствует действительности.
Самый распространенный подход — нормальное распределение , предполагающее, что вероятность выпадения значений постепенно падает с удалением от среднего. Хотя в реальных процессах нормальное распределение часто лучше всего описывает поведение параметров, у него есть неудобства в реализации. Во-первых, оно не ограничивает возможные отклонения от среднего. Пусть и с маленькой вероятностью, но значение параметра может оказаться сколь угодно далеким от ожидаемого. Из-за этого нормальное распределение иногда заменяют треугольным. Во-вторых, нормальное распределение с одинаковой вероятностью допускает отклонения параметра вверх и вниз от ожидаемой величины. Но часто вероятности снижения и роста показателя не одинаковы. Тогда может потребоваться более сложный закон распределения.
Шаг 4. Свойства распределения
Для выбранного закона распределения случайных параметров необходимо получить свойства этого распределения. В наиболее популярном нормальном распределении это среднее значение и стандартное отклонение. Если Монте-Карло будет использовать другое распределение, то и перечень его свойств может меняться.
Самая интересная (и сложная) деталь на этом шаге — корреляция . Если параметров несколько, то может оказаться, что они хотя и являются случайными, но их случайные колебания связаны друг с другом. Например, если при моделировании инвестиционного проекта в качестве случайных параметров выбраны цены готовой продукции и стоимость комплектующих, то жизненный опыт подсказывает, что чаще всего цены на товар и цены на комплектующие к нему меняются похожим образом, то есть эти величины коррелированы. Анализ их случайных колебаний без учета такой связи может заметно исказить картину.
Шаг 5. Многократный расчет
С помощью средств автоматизации расчетов (Excel, Python и т. п.) запускаем цикл из большого числа повторений, на каждом шагу которого получаем случайные значения параметров в соответствии с их законом распределения, вычисляем результат и накапливаем статистику по полученному результату.
Шаг 6. Анализ результатов
В первую очередь результаты моделирования представляют графически, отображая на гистограмме частоту попадания результата в разные интервалы значений. Далее можно рассчитать для результата любые статистические характеристики как для реального случайного процесса: среднее, стандартное отклонение и другие показатели.
Сложности применения Монте-Карло
Главная проблема анализа методом Монте-Карло связана с получением данных о статистическом распределении параметров, использованных в анализе. Сложный и насыщенный данными метод моделирования создает у аналитика впечатление о точности и глубине исследования возможных результатов, но в действительности качество сделанных выводов полностью зависит от качества исходных данных .
В ряде случаев для параметров доступны обширные данные наблюдений, и их статистику можно объективно рассчитать. Но часто наблюдения для параметров недоступны, и правила их распределения определяют аналитически. В таких ситуациях можно сделать две ошибки.
Ошибка 1. Неверное правило распределения. Закон распределения и его характеристики не стыкуются с тем, как определи базовые значения параметров. Например, продажи уже и так спланированы по наиболее оптимистическому сценарию, а статистическое распределение в равной степени допускает отклонения как вверх, так и вниз.
Ошибка 2. Игнорирование корреляции. Многие параметры, хотя и являются случайными, сильно связаны друг с другом. Если мы анализируем их как независимые, то можем получить сильно искаженный результат.
Организация расчета методом Монте-Карло в Excel
Наиболее распространенная среда, в которой выполняют анализ Монте-Карло — Excel. Сложные инструменты моделирования Монте-Карло, учитывающие все тонкости статистики, встроены в различные надстройки статистического анализа, такие как @RISK. Но они могут быть довольно дорогими, а если доступные данные не позволяют получить детальные параметры, то применение сложных инструментов не будет оправданным.
Простые решения для анализа Монте-Карло можно реализовать своими силами. Ниже приведены два видеоролика о том, как создать модель анализа Монте-Карло средствами таблиц данных или с применением макросов.
1. Вариант с использованием таблиц данных:
Файл из видео: monte-carlo-datatable.zip
2. Вариант с использованием макросов:
Файл из видео: monte-carlo-macro.zip
Такие статьи мы публикуем регулярно. Чтобы получать информацию о новых материалах, а также быть в курсе учебных программ, вы можете подписаться на новостную рассылку.
Если вам необходимо отработать определенные навыки в области инвестиционного или финансового анализа и планирования, посмотрите программы наших семинаров.
Источник